Файл: Бизнесом.docx

Если в полученную формулу вместо выражения К_н • rподставить равное ему значение из табл. 4.2, то можно получить вто­рую параметрическую модель, адекватную первой. Она будет иметь следующий вид:
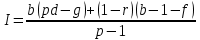(4.6)

Обе модели равнозначны, и выбор какой-то из них для кон­кретного прогнозирования прибыли зависит от обстоятельств и наличия исходной информации.

Проведем экспериментальную проверку точности полученных математических моделей с использованием конкретных данных условного примера. Пусть в базовом периоде предприятие имело следующие показатели деятельности:

• объем производства и реализации продукции N₆ = 1200;

• цена реализации единицы продукции Ц_б = 11,5;

• себестоимость единицы продукции С_б = 9,8.

• переменные затраты на единицу продукции С_пер = 5,5;

• условно-постоянные затраты С_пос = 5160.

По исходным данным по формуле 4.2 определим прибыль предприятия:

П_б = 1200 (11,5  9,8) = 2040.

В анализируемом периоде получены следующие результаты:

N_a= 1365; Ц_а = 11,7; К_н = 0,97; ∆ С_пос = 965.

По имеющимся данным определим себестоимость единицы продукции в анализируемом периоде С_а (формула 4.12):


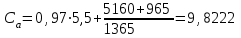
Теперь по формуле 4.3 можно определить прибыль предприятия в анализируемом периоде:

П_а = 1365 (11,7 — 9,8222) = 2563,2.

Отсюда легко определяется индекс прибыли по формуле 4.1:



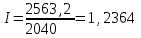
Проверим, совпадут ли результаты расчета индекса прибыли. прямым счетом (как было уже сделано) и путем использования двух параметрических моделей. Для этого предварительно опре­делим по соответствующим формулам необходимые коэффици­енты: р = 11,5 : 9,8 = 1,1735; b = 1365 : 1200 = 1,1375; d = 11,7 : 11,5 = 1,01739; r = 5,5 : 9,8 = 0,5612; f = 965 : 5160 = 0,18702; g= 0,97 • 0,5612 + (1 — 0,5612) = 0,98316.

Используя полученную информацию, определим индекс прибыли по формулам 4.5 и 4.6:




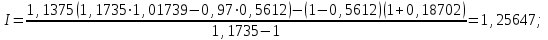
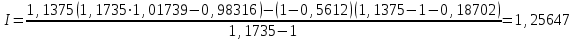
Как видим, полученные результаты точно совпали, что свидетельствует о точности полученных параметрических моделей. Однако вспомним, что параметрические модели типа 4.5 и 4.6 были получены для предприятий, выпускающих продукцию од­ного наименования (одной номенклатурно-ассортиментной по­зиции) или многих наименований, но формирующих опреде­ленный комплект. И хотя таких предприятий немало (например, предприятия горнодобывающих отраслей, нефтеперерабатывающей и

---

газодобывающей промышленности, леспромхозы и т.п.), они все же занимают незначительный удельный вес среди всех действующих предприятий. Возникает вопрос можно ли воспользоваться такими моделями для предприятий, выпускаю­щих более одной номенклатурно-ассортиментной позиции про­дукции? Математические расчеты показали, что можно. Но при этом значения входящих в модели параметров должны опреде­ляться по формулам из табл. 4.3. Они учитывают структурные сдвиги выпускаемой предприятием продукции при переходе из базового в анализируемый период.

Формулы табл. 4.3 учитывают по указанным периодам сле­дующее количество выпускаемой продукции:

т — количество номенклатурно-ассортиментных позиций выпускаемой продукции базового периода, снимаемой с производ­ства в анализируемом периоде;

п — количество номенклатурно-ассортиментных позиций выпускаемой продукции в базовом и анализируемом периодах (полностью сопоставимая продукция);

L — количество номенклатурно-ассортиментных позиций вновь освоенной продукции, выпускаемой только в анализируе­мом периоде.

Таблица 4.3

Формулы для определения параметрических

показателей, формирующих прибыль предприятия, в многономенклатурном производстве

Показатели	Вид формулы	Номер формулы
1	2	3
Коэффициент b		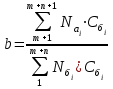4.15
Коэффициент р		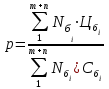4.16
Коэффициент d		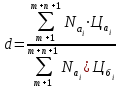4.17
Коэффициент g		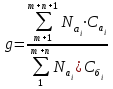4.18

---

Окончание табл. 4.3

Коэффициент r		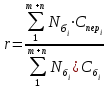4.19
Коэффициент f		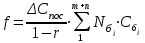4.20

Индекс «i» означает номер номенклатурно-ассортиментной позиции товар­ной продукции, выпускаемой в базовом и анализируемом периодах.
Использование полученных параметрических моделей позво­ляет решать многие теоретические и прикладные функциональ­ные задачи информационно-индикативного направления.
4.3. Исследование закономерностей изменения

прибыли предприятия

Определение прибыли предприятия путем прямого счета позволяет получить информацию о ее искомой величине только для, од­ного рассматриваемого варианта. Однако такой расчет не дает возможности установить закономерность изменения прибыли, если какой-то (или какие-то) параметр будет варьировать. Такую возможность можно получить только при использовании для исследовательских целей полученных параметрических моделей типа 4.5 и 4,6.

Возьмем модель типа 4.6 и покажем на примере изменения объемов производства и реализации товарной продукции закономерность изменения прибыли предприятия.

Предположим, что в базовом периоде предприятие имело коэффициент рентабельности p = 1,16 и коэффициент перемен­ных затрат r = 0,6. С целью повышения эффективности производства предприятие запланировало внедрить ряд мероприятий по снижению затрат на производство продукции. Это позволит ему получить соответствующий коэффициент изменения себестоимости g = 0,98. Одновременно для повышения спроса на свою продукцию, предприятие решило снизить на нее цены и получить соответствующий коэффициент в размере d= 0,95.

Определим, как изменится прибыль предприятия при изме­нении объемов производства и реализации продукции.

По формуле 4.6 определим индекс прибыли предприятия только для одного варианта, когда объем производства увеличит­ся на 15% (т.е. b = 1,15) при неизменных условно-постоянных за­тратах (т.е. f= 0).



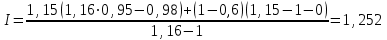
Таким образом, несмотря на то, что предприятие снизит це­ну реализации своей продукции на 5%, его прибыль возрастет по сравнению с базовым периодом на 25,2%.

---

По аналогии можно рассчитать индекс прибыли для других значений объемов производства и реализации продукции, начи­ная с b= 1,0 до b = 1,45 с шагом изменения этого коэффициен­та 0,05. Результаты расчетов представлены в табл. 4.4.

Таблица 4.4
Закономерность изменения индекса прибыли предприятия с изменением объема производства и реализации продукции

Исходные данные	p = 1,16			r = 0,6			d = 0,95			g= 0,98			f =0,0
Коэффициент b	1,0	1,05	1,10		1,15	1,20		1,25	1,30		1,35	1,40		1,45	1,50
Индекс прибыли I	0,76	0,92	1,08		1,25	1,41		1,57	1,74		1,90	2,06		2,23	2,39

---

Полученные результаты свидетельствуют о том, что если, во-первых, объем производства и реализации продукции в анализи­руемом периоде оставить на уровне базового периода, то про­изойдет существенное снижение прибыли, примерно на 24% (при b= 1,0; I= 0,762). Во-вторых, с ростом объема производства продукции на каждые 0,05 пункта индекс прибыли растет значи­тельно быстрее и составляет примерно 0,163 пункта, т.е. налицо опережение в три с лишним раза. Это свидетельствует о высокой эффективности управленческих решений, связанных с увеличе­нием объема производства и реализации товарной продукции.

Хотя табличная информация и дает некоторое представление об искомой закономерности изменения прибыли предприятия, она значительно уступает графику. Информационная емкость графического представления искомой закономерности столь ве­лика и значима, что о ней следует повести особый разговор.

Графическая иллюстрация расчетов прибыли открывает принципиально новые возможности в анализе, в исследованиях, при поиске закономерностей и предельных границ изменения отдель­ных прибылеобразующих параметров. Поэтому графика — важная составляющая познания причинно-следственных связей и глубо­кого понимания программирования и прогнозирования прибыли предприятия. Ее освоение, умение пользоваться ее возможностями открывает перед управленческими службами любого предприятия новые горизонты поиска и реализации резервов повышения при­были и эффективности производства.

На рис. 4.1 представлен один из возможных вариантов изо­бражения индекса прибыли с помощью графического метода, обладающего высокой информационной емкостью. Рисунок со­стоит из двух частей — верхней и нижней. Верхняя часть связы­вает между собой изменения в цене и себестоимости продукции. Первый из указанных параметров обозначен — d, второй — g. Количественное сочетание этих параметров обеспечивает вход в нижнюю часть рисунка, состоящую из двух зон и четырех под­зон. Первая и вторая подзоны — часть графика, расположенная левее нулевой вертикальной линии, третья и четвертая подзо­ны — правее от этой вертикали.

Левая зона — зона рентабельного, прибыльного производст­ва, правая зона — убыточного производства. Но и в этих зонах не все части равнозначны.

Первая подзона — это рост прибыли, процветание и благо­получие, успех предприятия и всей его деятельности. Попадание во вторую подзону означает падение прибыли по сравнению с базовым периодом. Это как бы предостережение предприятию о грозящей ему опасности: будьте осторожны, взвешивайте свои управленческие решения, подумайте о последствиях!

---