Файл: Бизнесом.docx

Расчеты индекса прибыли при структурных сдвигах следует производить по тем же параметрическим моделям типа 4.5 или 4.6 с небольшой разницей, учитывающей эту характерную осо­бенность производства. Модификации этих моделей выгладят следующим образом:

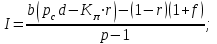(4.21)
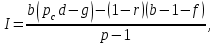(4.22)

где p_с — коэффициент рентабельности производства, учиты­вающий структурные сдвиги.

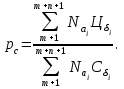(4.23)
Все представленные в формуле 4.23 параметры имеют тот же экономический смысл, что и в формулах 4.2 и 4.3, но взяты по конкретным позициям продукции.

После подготовки всей необходимой информации считыва­ется индекс прибыли, по которому можно судить, насколько удачным оказались проведенные структурные сдвиги. Очень часто при этом результаты расчета отличаются от ожидаемых и порой выглядят парадоксальными. Вот конкретный пример. Пусть предприятие в базовом периоде выпускало и предполагает выпускать в анализируемом периоде три вида сопоставимой продукции (т.е. n = 3при т = 0 и L = 0). Коэффициент переменных затрат r = 0,3. Остальные исходные данные по видам продукции представлены ниже.

Базовый период	Объем производства, тыс. шт.	80	250	100
	Цена реализации, руб./шт.	6,3	8,7	10,4
	Себестоимость, руб./шт.	5,1	7,2	12,5
Анализируемый период	Объем производства, тыс. шт.	80	250	х
	Цена реализации, руб./шт.	6,3	8,7	10,4
	Себестоимость, руб./шт.	5,1	7,2	12,5

Из приведенных данных видно, что первые два вида продук­ции рентабельны, их производство и реализация приносят пред­приятию прибыль (так как цена превышает себестоимость). Иначе обстоит дело с третьим видом продукции. Она убыточна. Производство и реализация каждой единицы такой продукции приносят предприятию убыток в размере 2,1 руб./шт., ибо цена ее реализации ниже себестоимости.

---

Возникает вопрос: как поступить предприятию, чтобы повы­сить прибыльность производства? Сокращать ли производство убыточной продукции или, наоборот, увеличивать его? Именно поэтому в строке «объем производства» для анализируемого пе­риода среди исходных данных примера стоит неизвестная вели­чина x.

Чтобы разрешить этот вопрос, обратимся к параметрической модифицированной модели. Проведенные расчеты дали сле­дующие результаты:

Объем производства убыточ­ной продукции x, тыс. шт.	0	25	50	75	100	125	150
Индекс прибыли	− 1,54	−0,91	−0,27	0,36	1,0	1,64	2,27

Из приведенных данных видно, что с увеличением произ­водства убыточной продукции при фиксированных для этого примера исходных данных индекс прибыли возрастает.

Если в базовом периоде предприятие получило прибыль в размере

80000 (6,3−5,1) + 250000 (8,7 − 7,2) + 100000(10,4 − 12,5) = 261000 руб., то, изменив объем производства и реализации третьего вида продукции, прибыль составит:

при x = 0 → (−1,54) · 261000 = − 401940 руб.;

приx = 50 → (− 0,27) · 261000 = − 70470 руб.;

при x = 75 → 0,36 · 261000 = 93960 руб.;

при x = 100 → 1 · 261000 = 261000 руб.;

при x = 125 → 1,64 · 261000 = 428040 руб.;

при x = 150 → 2,27 · 261000 = 592470 руб.

Как видно из расчетов, если вообще снять с производства убы­точную продукцию, то предприятие понесет от всей своей дея­тельности убыток в размере примерно 402 тыс. руб. и доведет свою прибыль до 593 тыс. руб. при расширении производства в 1,5 раза.

Не будем вдаваться в анализ полученных результатов и предос­тавим читателю самому объяснить их экономический смысл. По­путно предлагаем ответить на ряд вопросов: 1) какой внутрипроизводственный механизм оказывает столь сильное влияние на вели­чину прибыли? 2) всегда ли найденная закономерность изменения прибыли будет иметь место в производстве, и если нет, то какой исходный параметр и на какую величину надо изменить

---

, чтобы за­кономерность формирования прибыли превратилась в свою пря­мую противоположность? 3) в каких видах производства можно с успехом применять столь оригинальный метод обогащения?

Такие неожиданные результаты можно получить в практике функционирования предприятий довольно часто, в том числе вследствие Изменения структуры продукции. Поэтому использова­ние параметрической модели может предотвратить нерациональ­ные планово-управленческие решения, сберечь предприятиям зна­чительные средства, уберечь от непредусмотренного ущерба.
4.10. 3оны принятия планово-управленческих решений

Каждое принятое, а затем и реализованное управленческое ре­шение приводит к определенным экономическим результатам, из которых наиважнейшим является показатель прибыли. Ни одно предприятие, фирма не останется равнодушным к вопросу о том, какая у них ожидается прибыль. Она может быть такой же или больше той, что была в базовом периоде, или понизиться, достиг­нув нулевого значения. Наконец реальной для каждой производственно-структурной единицы может оказаться ситуация, когда при­быль становится отрицательной, а производство убыточным.

Следовательно, можно четко выделить три основные зоны экономического состояния любого предприятия: 1) прибыль положительна и растет (I> 1); 2) прибыль положительна, но при этом уменьшается (0 < I<1); 3) прибыль уменьшается и стала отрицательной (I< 0).

Между этими зонами имеются границы, которые однозначно определяются количественно. Так, граница между первой и вто­рой выделенными зонами четко определяется индексом прибы­ли I = 1, а граница между второй и третьей зонами проходит при величине индекса прибыли I = 0.

Принимая то или иное планово-управленческое решение, нужно сразу стремиться к такому варианту, у которого индекс прибыли будет попадать в определенную, заранее выбранную зону. Что для этого необходимо? Прежде всего задаются показа­тели работы предприятия в базовом периоде. Они известны, по­скольку факт прошлого производства уже свершился, и, стало быть, установить их не представляет особого труда. Такими по­казателями являются коэффициент рентабельности производст­ва pи коэффициент переменных затрат r. Затем выясняется, предполагается ли модернизация производства (реконструкция, техническое перевооружение, расширение и пр.), и если нет, то принимается показатель f= 0, а если да — то

---

f> 0.

После этого остаются три прибылеобразующих параметра: коэффициент изменения цены товара d, коэффициент измене­ния себестоимости продукции g , коэффициент изменения объе­ма производства продукции b. Один из этих параметров жестко задается в процессе принятия решения, а два других составляют, так называемую ключевую пару. Параметры, их составляющие, взаимосвязаны: изменение одного параметра влияет на величину другого. Следовательно, эти параметры будут соотноситься меж­ду собой как аргумент и функция. Это и дает возможность оп­ределить значения координат точек, совокупность которых со­ставит границу соответственно между первой и второй, а также между второй и третьей зонами.

Итак, два параметра из трех рассматриваемых принимаются в качестве ключевых. Поэтому здесь возможны три различных комбинации ключевых параметров из трех имеющихся: сочета­ние цены dи объема производства b, сочетание цены dи затрат g, и сочетание затрат gи объема производства b.

За основу рассмотрения примем первый вариант сочетания клю­чевых параметров, ибо именно он представляет наибольший практи­ческий интерес. Поэтому в дальнейшем объектом нашего внимания становятся ключевые прибылеобразующие параметры dи b.

С помощью параметрической модели типа 4.6, задав парамет­ры p, r, Iи g, определим координаты точек кривых, которые будут находиться между первой, второй и третьей зонами, являясь при этом границами между ними (рис. 4.4).

Смысл выделенных зон тот же, что и для прошлых рисунков. Первая зона — зона рентабельного производства, в которой прибыль, по сравнению с базовым периодом, возрастает. Вторая ― зона — зона падения прибыли, хотя производство остается рен­табельным. И наконец, третья зона — зона убыточного произ­водства.

Внутри одной из указанных зон (в зависимости от того, ка­кой индекс прибыли будет задан) можно построить кривую без­различия. Все точки этой кривой будут соответствовать задан­ному индексу прибыли.

Приняв то или иное значение коэффициента изменения це­ны, можно определить объем производства и реализации про­дукции, который и должен обеспечить заданную величину ин­декса прибыли.

Например, если принять p = 1,15, r = 0,5, g = 1, I= 1,7, то, как видно из рисунка, можно взять любое сочетание параметров ключевой пары, а именно:

---

при d= 1,1 → b = 0,987;

при d= 1,0 → b = 1,16;

при d= 0,95 → b = 1,274;

при d= 0,85 → b = 1,581 и т.д.


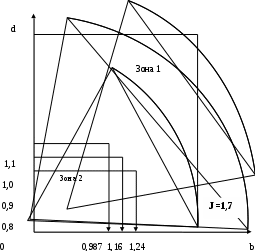
Рис. 4.4. Зоны принятия планово-управленческих решений:

p = 1,15; r = 0,5; g = 1
В таких сочетаниях и будет обеспечиваться заданный индекс прибыли I = 1,7. Объем производства, который при заданной цене обеспечивает искомую прибыль, обозначим b_п.

Но каждое предприятие, как известно, обладает определенной производственной мощностью, и этот объем производства, кото­рый будет соответствовать мощности предприятия, обозначим b_м.

Наконец, объем производства, при котором эффективность капитальных вложений, направленных на получение заданной прибыли, будет не ниже фирменного норматива, обозначим b_э.

Итак, есть величина производственной программы b_п, кото­рая задается исходными условиями, и есть два ограничения b_ми b_э.Как соотносятся все эти три значения объема производства в различных условиях производства — знать крайне необходимо. Это чрезвычайно важная информация, использование которой при выработке планово-управленческих решений позволит из­бежать ошибок.

Все возможные соотношения между указанными объемами рассмотрены и проиллюстрированы на рис. 4.5. Всего оказыва­ется четыре случая разных соотношений.

Первый случай — b _м < b_n < b_э .

Второй случай — b _n < b_м < b_э .

Третий случай — b_n < b_э < b_м.

Четвертый случай: — b_э < b_n < b_м .


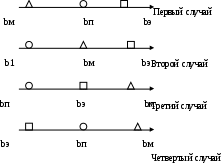
Рис. 4.5. Ограничения в управленческих решениях

по объему производства продукции
Вполне очевидно, что самым лучшим и приемлемым реше­нием будет такое, когда производственная программа по прибыли окажется, с одной стороны, больше минимальной границы эффективности, а с другой — меньше производственной мощ­ности предприятия. Такому условию соответствует только четвёртый случай. Его характерная особенность заключается в том, что точка, соответствующая необходимой производственной программе и обеспечивающая заданную прибыль, находится внутри зоны возможного принятия решения. Данная точка обладает большей эффективностью, чем установлено нормативом фирмы, но одновременно она находится внутри производствен­ных возможностей предприятия по его мощности.

---