Файл: Бизнесом.docx

Если просуммировать обе составляющие себестоимости, то закономерность ее изменения по мере насыщения производства основными производственными фондами отображается кривой, у которой вначале наблюдается падение текущих затрат до опре­деленного уровня, а затем, перейдя точку перегиба, затраты начнут возрастать. Это и будет кривая изменения себестоимости продукции в зависимости от размера капитальных вложений в производство (кривая С).

Выделим на этой кривой три точки: 1, 2 и 3. Точка 1 соот­ветствует минимальному значению себестоимости выпускаемой продукции. Точки 2 и 3 имеют себестоимость продукции выше, чем у точки 1. Но если точка 2 и проигрывает точке 1 в себе­стоимости, зато она выигрывает на капитальных затратах, пред­ставляя тем самым для инвестора определенный интерес. Поэтому необходимо рассматривать точку 2 как альтернативу точке 1, ибо обе они в чем-то выигрывают, а в чем-то проигры­вают друг другу (выигрыш в себестоимости и проигрыш в капи­тальных затратах, и наоборот).

Иначе обстоит дело с точкой 3: она проигрывает точке 1 и в себестоимости, и в капитальных затратах. Следовательно, такая точка не представляет интереса ни для предпринимателя, ни для инвестора. Она по всем статьям проигрывает точке 1, а потому из дальнейшего анализа исключается как не соответствующая требованиям эффективности. Поэтому надо считать точку 1 правой границей рассматриваемых и включаемых в анализ эф­фективности вариантов вложений. Все точки, лежащие левее этой границы, могут представлять экономический интерес и должны включаться в сравнительный анализ для выбора луч­шего из рассматриваемых вариантов.

В дальнейшем мы будем рассматривать только две точки — 1 и 2. Точка 1 — единственная в своем роде, определяющая границу эффективности вложений, а точка 2 — является предста­вителем любой возможной альтернативной точки, которая может оказаться более привлекательной, чем точка 1. Дальнейший анализ сравнительной эффективности вложений на примере двух указанных точек можно рассматривать как необходимый и достаточный.

Итак, первый вопрос, который возникает в процессе анали­за: какой из двух рассматриваемых альтернативных вариантов является более предпочтительным по чисто экономическим со­ображениям? Напомним, что по всем остальным признакам оба этих варианта полностью удовлетворяют и предпринимателя, и возможного инвестора.

---

Построим наши рассуждения следующим образом. Если вне­дрить первый вариант, отказавшись при этом от второго, то за год можно сэкономить на себестоимости продукции величину (С₂ — С₁). Эта экономия, разумеется, сравнительная, ибо пока­зывает, какой выигрыш получит предприниматель, отдав пред­почтение первому варианту. Однако есть не только выигрыш, но и проигрыш. Внедряя первый вариант, предприниматель несет более весомые капитальные затраты по сравнению со вторым вариантом, и этот проигрыш можно точно подсчитать. Он составит (К₁ — К₂) или, как говорят экономисты, его внедрение потребует дополнительных капитальных вложений в размере ∆К.

Остается соизмерить полученную выгоду с дополнительными единовременными вложениями от внедрения первого варианта, по сравнению со вторым. Это можно сделать, если взять отношение получаемого эффекта и дополнительных капитальных затрат:

(С₂ — С₁) : (К₁ — К₂).

Такое соотношение называется коэффициентом сравнительной экономической эффективности дополнительных капитальных вложении. Величину этого коэффициента можно записать в виде следующей формулы:

Е = (С₂ — С₁) :(К₁— К₂), (7.8)

где Е — величина искомого коэффициента эффективности;

С₁ и С₂ — соответственно себестоимость годового объема производства продукции в руб./год по первому и второму вари­антам;

К₁ и К₂ — соответственно капиталовложения в первый и второй варианты, руб.

Иногда вместо коэффициента эффективности определяют обрат­ное ему выражение — показатель срока окупаемости дополнительных капитальных затрат. Его величина рассчитывается по формуле

Т = (К₁— К₂) : (С₂— С₁), (7.9)

где Т — срок окупаемости дополнительных капитальных вложений, лет.

Рассчитав показатель коэффициента эффективности по формуле 7.8 или срока окупаемости по формуле 7.9, еще невоз­можно ответить на вопрос, какой из двух вариантов наилучший. В величине этих показателей такого ответа не содержится, ибо непонятно, к какому из двух вариантов относятся полученные цифровые результаты.

Чтобы ответить на главный вопрос, ради которого все эти расчеты проводились, необходимо сравнить полученные расчет­ные показатели с заранее установленным нормативом. Их обо­значают соответственно Е_ни Т_н. Тогда условие выгодности бо­лее капиталоемкого варианта можно представить в виде сле­дующих неравенств:

---

Е > Е_н или Т < Т_н . (7.10)

Указанные условия лучше всего изобразить в виде следующих выражений (напомним, что это будут условия выгодности более капиталоемкого варианта по сравнению с менее капиталоемким из двух рассматриваемых и сопоставляемых между собой):

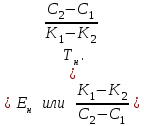(7.11)

В дальнейшем в основном будем пользоваться первой из представленных формул, т.е. формулой коэффициента сравни­тельной эффективности дополнительных капитальных вложений.

Итак, как же пользоваться этими формулами?

Пусть имеются два альтернативных варианта вложений. По первому варианту себестоимость производства продукции за год составляет С₁= 10000 руб., а по второму варианту тот же показа­тель пусть будет равен С₂ = 12000 руб. Потребность в капиталь­ных вложениях будет соответственно равна К₁ = 200000 руб. и К₂ = 190000 руб.

Определим коэффициент эффективности по формуле 7.8:

Е= 12000 -10000 : 200000  190000 = 2000 :10000 = 0,2 .

О чем говорит полученная величина? Она свидетельствует, что дополнительные капитальные вложения дадут отдачу в раз­мере 0,2 руб. экономического эффекта от снижения себестоимо­сти продукции на каждый рубль дополнительных вложений. Но опять-таки хорошо это или плохо — сказать невозможно, и ка­кой из двух рассматриваемых вариантов лучше — тоже неясно.

Чтобы ответить на этот главный вопрос, обратимся к норма­тиву эффективности. Пусть он будет Е_н= 0,15. Тогда в соответ­ствии с формулой 7.11, можно утверждать, что более выгодным будет более капиталоемкий вариант, т.е. в данном случае это бу­дет первый вариант, ибо в соответствии с формулой 7.10 0,2 > 0,15. Обратим внимание на то, что если норматив будет принят на уровне Е_н = 0,25, то более выгодным станет менее капиталоемкий вариант — в данном случае второй.

Из изложенного вытекает очень важное следствие: при вы­боре лучшего варианта из двух рассматриваемых большое значе­ние имеет величина принятого норматива эффективности до­полнительных вложении, т.е. норма Е_н.

Каково должно быть значение норматива эффективности, как установить его величину? Ведь от этого один и тот же вариант мо­жет быть принят к внедрению или отвергнут как неэффективный.

В условиях планово-директивной системы хозяйствования значение норматива эффективности

---

Е_нустанавливалось государ­ством в централизованном порядке и примерно соответствовало средней норме рентабельности основных производственных фондов в народном хозяйстве. Последняя такая норма в услови­ях СССР была установлена на уровне E_н= 0,15.

В условиях рынка каждая фирма должна установить для себя значение такого норматива самостоятельно и независимо от других фирм.

Чем же руководствуются фирмы при определении величины норматива эффективности дополнительных капитальных вложе­ний? Ответить на этот вопрос за все фирмы, работающие в рынке, практически невозможно. У каждой из них могут быть в каждый данный момент свои особые проблемы, возможности, потребности в капитальных вложениях, свободные денежные ресурсы и, наконец, просто собственные представления о том, какой должна быть норма эффективности вложений.

И все же можно дать определенную рекомендацию, без учета которой ни одна фирма не будет устанавливать для себя норму эффективности капитальных вложений. Такая рекомендация учитывает чистые дивиденды, которые выплачивает на вложен­ные денежные средства по годовому депозиту высоконадежный коммерческий банк. Тогда у предпринимателя появляется аль­тернатива несколько иначе использовать свободные денежные ресурсы, получая гарантированный доход от их вложений на один год в указанный банк. При этом предприниматель рассуж­дает примерно так. Можно вложить деньги в конкретный проект, который при его реализации принесет на каждый рубль капиталь­ных затрат эффект на экономии текущих затрат, скажем, 0,3 руб. Однако можно не вкладывать свободные деньги в проект, а поло­жить их в банк и гарантированно получать на внесенные деньга чистые дивиденды в размере, скажем, 0,2 руб. Следовательно, последняя цифра и будет тем самым ориентиром, с которым предприниматель будет сопоставлять свои возможные доходы от реализации проектного решения.

Если получаемые от проекта доходы будут больше, чем он может получить в банке, то следует, очевидно, вкладывать деньги в реализацию проекта. Если проект даст доход меньше, чем га­рантирует банк, то лучше вкладывать деньги именно в банков­ский депозит. Отсюда ясно, что гарантированный дивиденд и есть тот самый норматив эффективности дополнительных капи­тальных вложений, который в первом приближении может при­нять фирма для решения своих предпринимательских задач в соответствии с условием формулы 7.11.

Разумеется, каждая фирма может установить определенную поправку на величину такого норматива. Например, она может учесть риск вложений в проект, и тогда норма эффективности вложений несколько возрастет. Вообще можно порекомендовать формулу для определения величины указанного норматива:

---

Е_н = Е _г + Е_р + Е _п , (7.12)

где Е_н— норматив сравнительной экономической эффек­тивности дополнительных капитальных вложений;

Е_г— гарантированная норма доходности вложений в вы­соконадежный коммерческий банк;

Е_р — дополнительная страховая норма, учитывающая риск вложений в проект (эта норма должна учитывать страхова­ние проектной деятельности, и от полноты страховки норматив будет либо равен нулю, либо примет значительные размеры);

Е_п— минимальная предельная норма доходности вложе­ний, которая принимается предпринимателем для положитель­ного решения о дополнительных вложениях в реализацию ото­бранного варианта проекта.

По экономической сущности последнее слагаемое формулы 7.12 и есть тот самый дополнительный эффект от снижения се­бестоимости продукции при реализации более капиталоемкого варианта, ради которого он и принимается к внедрению. Два первых слагаемых при этом играют роль воспроизведения гаран­тированного дохода от вложений денежных средств ввысокона­дежный банк.

Приведенные затраты и область использования этого показа­теля при оценке проектов. Разобравшись с нормативом эффек­тивности, вернемся к формуле 7.11. С ее помощью можно вы­яснить целесообразность внедрения того или иного варианта из двух рассматриваемых.

А что, если таких вариантов будет более двух? Как быть с отбором лучшего из них? В этом случае можно поступить сле­дующим образом. Отбираются два любых варианта и с помощью расчета по указанной формуле определяется, какой из них луч­ший. Этот вариант сравнивается с любым другим альтернативным вариантом по той же формуле 7.11. Из новой пары вариан­тов опять можно отобрать лучший, и так до тех пор, пока не бу­дет найден самый лучший вариант из всех предложенных к ана­лизу и рассмотрению.

Надо отметить, что подобная схема отбора лучшего варианта не очень удобна в техническом плане, поскольку нередко аль­тернативных вариантов бывает довольно много и выполнять описанную процедуру не очень удобно. Например, когда решал­ся вопрос о строительстве в СССР завода по производству лег­ковых автомобилей в конце 60-х годов мощностью 660 тыс. ав­томобилей в год, то рассматривалось 70 различных вариантов размещения этого предприятия на территории страны. Естест­венно, проводить парные сравнения было неудобно, а глав­ное — нецелесообразно, ибо при этом терялась очень важная информация о рейтинге каждого альтернативного варианта.

---