ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 53
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Элементы матрицы, имеющие равные индексы, образуют главную диагональ матрицы.
Определение 8.22. Квадратная матрица называется диагональной, если все элементы вне ее главной диагонали равны нулю.
Определение 8.23. Диагональная матрица n -го порядка, у которой диагональные элементы равны единице, называется единичной матрицей n -го порядка и обозначается Е.
Определение 8.24. Матрица называется матрицей треугольного вида, если все элементы над (под) главной диагональю равны нулю.
Примеры.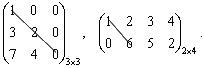
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 125–126.
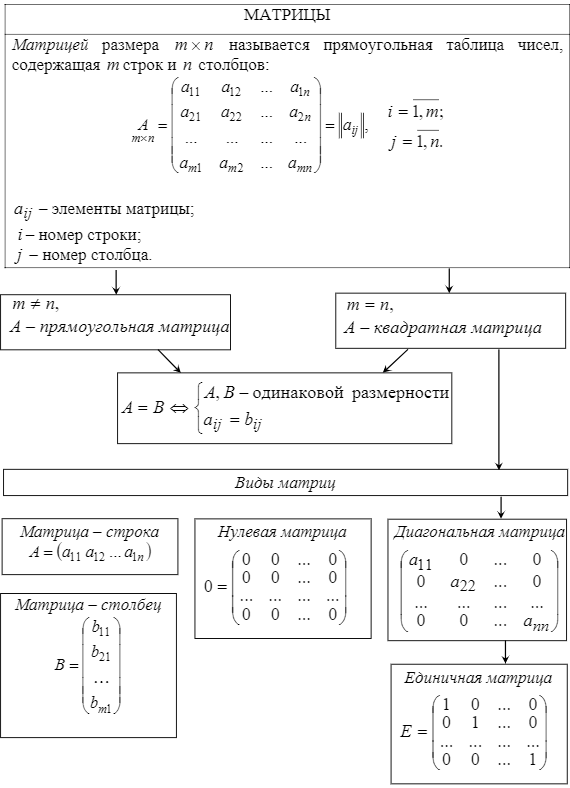
Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. - Ульяновск: ООО «Вектор-С», 2008. - С. 6, 10.
2. Определитель квадратной матрицы 3-го порядка может быть вычислен по правилу треугольников, или правилу Сарруса.
где соответствующие произведения элементов берутся либо со знаком «+» (левая схема), либо со знаком «–» (правая схема):
5.Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения:
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 11, 12.
Свойства определителей
Теорема 8.8.При транспонировании величина определителя не меняется.
Следствие. Строки и столбцы в определителе равноправны, т. е. свойства, справедливые для строк, будут справедливы и для столбцов.
Теорема 8.9.Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число.
Следствие. Постоянный множитель строки можно выносить за знак определителя.
Теорема 8.10.Если в определителе поменять местами две строки, то определитель сменит знак на противоположный.
Следствие 1. Определитель, у которого две строки равны, равен нулю.
Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю.
Теорема 8.11.Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т. д.
Следствие. Если строки определителя линейно зависимы, то такой определитель равен нулю.
Теорема 8.12.Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.
Миноры и алгебраические дополнения
Пусть дана прямоугольная матрица А размера m × n .
Определение 8.30. Минором порядка k данной матрицы, где k ≤ min (m; n), называется определитель k -го порядка, полученный из матрицы А вычеркиванием (m - k) строк и (n - k) столбцов.
Пример 8.13.
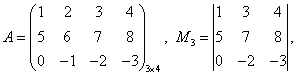
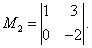
Определение 8.31. Дополнительным минором Mij к элементу aij квадратной матрицы An × n называется определитель (n - 1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен.
Пример 8.14.
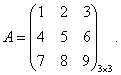
Найдем дополнительный минор к элементу a31 .
Определение 8.32. Алгебраическим дополнением Aij к элементу aij квадратной матрицы An × n называется число Aij = (- 1)i+j × Mij .
Пример 8.15. Найдем алгебраическое дополнение к элементу a33 .
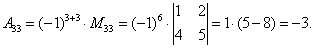
Теорема 8.13.Определитель равен сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения.
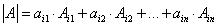- разложение определителя по i -й строке.
Теорема 8.14.Сумма попарных произведений элементов любой строки (столбца) определителя на алгебраические дополнения к соответствующим элементам другой строки (столбца) равна нулю.
Вычисление определителей порядка n > 3 сводится к вычислению определителей второго и третьего порядка с помощью теорем 8.12 и 8.13.
Пример 8.16.
разложение определителя по первому столбцу
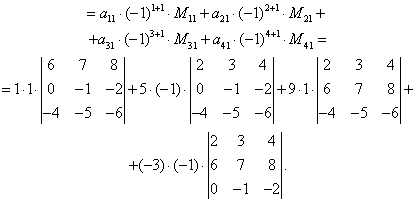
Перед разложением определителя для удобства получают в одном из столбцов нули. Это сокращает объемы вычислений. Для этого используют теорему 8.12. Одну из строк умножают на некоторые числа и складывают с другими строками.
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 131–134.
1.24. Вычислить определители матрицы A :
Решение:
а) По формуле
б) Определитель вычисляется по формуле (1.8). Запоминать эту формулу не следует, достаточно применить правило треугольников, согласно которому три произведения элементов, показанных на левой схеме (п. 2), берутся со знаком «+», а три других произведения элементов, показанных на правой схеме (п. 2), берутся со знаком «–»
| A | = 1 × 1 × 1 + 0 × 2 × 2 + 0 × 5 × 3 – 0 × 1 × 0 – 1 × 2 × 3 – 1 × 2 × 5 = –15.
1.25. Вычислить тот же определитель, приведенный в задаче 1.24 , б , используя его разложение по элементам: а ) первой строки; б ) второго столбца.
Решение:
а) Находим алгебраические дополнения элементов первой строки по формуле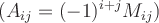
:
Теперь по теореме Лапласа (1.10) :
| A | = a11 × A11 + a12 × A12 + a13 × A13 = 1 × (– 5) + 2 × (– 5) + 0 × 15 = –15.
б) Находим алгебраические дополнения элементов второго столбца:
Теперь по формуле (1.8) :
| A | = a21 × A21 + a22 × A22 + a32 × A32 = 2 × (– 5) + 1 × 1 – 3 × 2 = –15.
1.26. Вычислить определитель матрицы четвертого порядка:
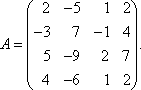
Решение: С помощью эквивалентных преобразований приведем матрицу A к треугольному виду. Если возможно, перестановкой строк (столбцов) добиваемся того, чтобы элемент a11 = 1. В данном случае достаточно поменять местами 1-й и 3-й столбцы; при этом меняется знак определителя матрицы A :
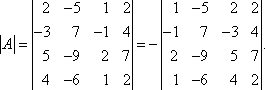
Умножая элементы 1-й строки на числа (–aij); i = 1, 2, 3, 4, т.е. в данном случае на числа 1, (–2), (–1), и прибавляя их соответственно к элементам 2-й, 3-й и 4-й строк, добиваемся того, чтобы все элементы 1-го столбца (кроме a11) равнялись нулю:
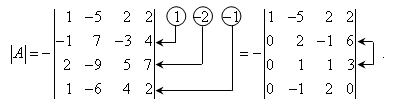
Далее, если возможно, перестановкой строк (столбцов) добиваемся, чтобы новый элемент a22 = 1. В данном случае это возможно, если переставить 2-ю и 3-ю строки; при этом меняется знак определителя. Умножая элементы 2-й строки, полученной матрицы на числа (–a12) (i = 3, 4), в данном случае на числа (–2) и 1, добиваемся того, чтобы все элементы 2-го столбца (кроме a22) равнялись нулю.
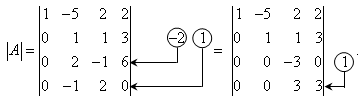
Для получения треугольной матрицы в данном случае достаточно прибавить элементы 3-й строки полученной матрицы к элементам 4-й. Определитель треугольной матрицы равен произведению ее диагональных элементов:
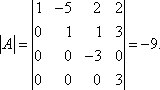
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 13–14.
Определение 8.22. Квадратная матрица называется диагональной, если все элементы вне ее главной диагонали равны нулю.
Определение 8.23. Диагональная матрица n -го порядка, у которой диагональные элементы равны единице, называется единичной матрицей n -го порядка и обозначается Е.
Определение 8.24. Матрица называется матрицей треугольного вида, если все элементы над (под) главной диагональю равны нулю.
Примеры.
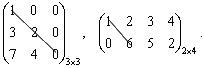
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 125–126.
Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. - Ульяновск: ООО «Вектор-С», 2008. - С. 6, 10.
2. Определитель квадратной матрицы 3-го порядка может быть вычислен по правилу треугольников, или правилу Сарруса.
где соответствующие произведения элементов берутся либо со знаком «+» (левая схема), либо со знаком «–» (правая схема):
5.Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения:
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 11, 12.
Свойства определителей
Теорема 8.8.При транспонировании величина определителя не меняется.
Следствие. Строки и столбцы в определителе равноправны, т. е. свойства, справедливые для строк, будут справедливы и для столбцов.
Теорема 8.9.Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число.
Следствие. Постоянный множитель строки можно выносить за знак определителя.
Теорема 8.10.Если в определителе поменять местами две строки, то определитель сменит знак на противоположный.
Следствие 1. Определитель, у которого две строки равны, равен нулю.
Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю.
Теорема 8.11.Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т. д.
Следствие. Если строки определителя линейно зависимы, то такой определитель равен нулю.
Теорема 8.12.Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.
Миноры и алгебраические дополнения
Пусть дана прямоугольная матрица А размера m × n .
Определение 8.30. Минором порядка k данной матрицы, где k ≤ min (m; n), называется определитель k -го порядка, полученный из матрицы А вычеркиванием (m - k) строк и (n - k) столбцов.
Пример 8.13.
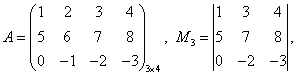
Определение 8.31. Дополнительным минором Mij к элементу aij квадратной матрицы An × n называется определитель (n - 1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен.
Пример 8.14.
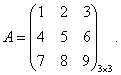
Найдем дополнительный минор к элементу a31 .
Определение 8.32. Алгебраическим дополнением Aij к элементу aij квадратной матрицы An × n называется число Aij = (- 1)i+j × Mij .
Пример 8.15. Найдем алгебраическое дополнение к элементу a33 .
Теорема 8.13.Определитель равен сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения.
- разложение определителя по i -й строке.Теорема 8.14.Сумма попарных произведений элементов любой строки (столбца) определителя на алгебраические дополнения к соответствующим элементам другой строки (столбца) равна нулю.
Вычисление определителей порядка n > 3 сводится к вычислению определителей второго и третьего порядка с помощью теорем 8.12 и 8.13.
Пример 8.16.
разложение определителя по первому столбцу
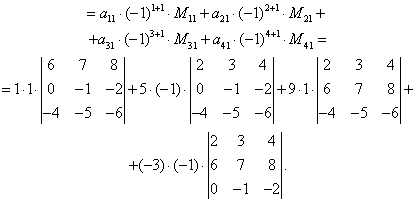
Перед разложением определителя для удобства получают в одном из столбцов нули. Это сокращает объемы вычислений. Для этого используют теорему 8.12. Одну из строк умножают на некоторые числа и складывают с другими строками.
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 131–134.
1.24. Вычислить определители матрицы A :
Решение:
а) По формуле
б) Определитель вычисляется по формуле (1.8). Запоминать эту формулу не следует, достаточно применить правило треугольников, согласно которому три произведения элементов, показанных на левой схеме (п. 2), берутся со знаком «+», а три других произведения элементов, показанных на правой схеме (п. 2), берутся со знаком «–»
| A | = 1 × 1 × 1 + 0 × 2 × 2 + 0 × 5 × 3 – 0 × 1 × 0 – 1 × 2 × 3 – 1 × 2 × 5 = –15.
1.25. Вычислить тот же определитель, приведенный в задаче 1.24 , б , используя его разложение по элементам: а ) первой строки; б ) второго столбца.
Решение:
а) Находим алгебраические дополнения элементов первой строки по формуле
: Теперь по теореме Лапласа (1.10) :
| A | = a11 × A11 + a12 × A12 + a13 × A13 = 1 × (– 5) + 2 × (– 5) + 0 × 15 = –15.
б) Находим алгебраические дополнения элементов второго столбца:
Теперь по формуле (1.8) :
| A | = a21 × A21 + a22 × A22 + a32 × A32 = 2 × (– 5) + 1 × 1 – 3 × 2 = –15.
1.26. Вычислить определитель матрицы четвертого порядка:
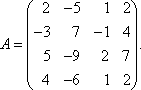
Решение: С помощью эквивалентных преобразований приведем матрицу A к треугольному виду. Если возможно, перестановкой строк (столбцов) добиваемся того, чтобы элемент a11 = 1. В данном случае достаточно поменять местами 1-й и 3-й столбцы; при этом меняется знак определителя матрицы A :
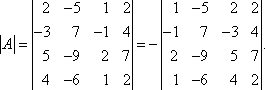
Умножая элементы 1-й строки на числа (–aij); i = 1, 2, 3, 4, т.е. в данном случае на числа 1, (–2), (–1), и прибавляя их соответственно к элементам 2-й, 3-й и 4-й строк, добиваемся того, чтобы все элементы 1-го столбца (кроме a11) равнялись нулю:
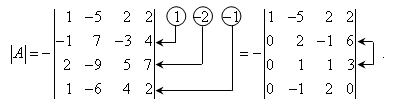
Далее, если возможно, перестановкой строк (столбцов) добиваемся, чтобы новый элемент a22 = 1. В данном случае это возможно, если переставить 2-ю и 3-ю строки; при этом меняется знак определителя. Умножая элементы 2-й строки, полученной матрицы на числа (–a12) (i = 3, 4), в данном случае на числа (–2) и 1, добиваемся того, чтобы все элементы 2-го столбца (кроме a22) равнялись нулю.
Для получения треугольной матрицы в данном случае достаточно прибавить элементы 3-й строки полученной матрицы к элементам 4-й. Определитель треугольной матрицы равен произведению ее диагональных элементов:
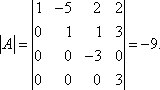
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 13–14.
