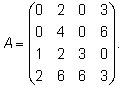ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 72
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 2. Метод решения систем линейных уравнений Крамера
Решение системы с помощью формул Крамера
Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:
Теорема 8.22.(теорема Крамера). Если определитель матрицы, составленной из коэффициентов при неизвестных, отличен от нуля (|A| ≠ 0), то система имеет единственное решение, которое можно найти по формулам Крамера:
где D =|A| - главный определитель,
Dj - j -й вспомогательный определитель, который получен из определителя D заменой j -го столбца столбцом свободных членов.
Пример 8.20.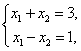
Для системы двух линейных уравнений с двумя неизвестными справедливы свойства:
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 145–146.
Рассмотрим систему уравнений:
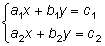(1)
Введем обозначения:
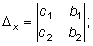
Если определитель системы Δ ≠ 0, то система (1) имеет единственное решение:
.
Пример: решить систему уравнений:
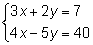
Решение:
Составим и вычислим определители:
.
Система имеет единственное решение:
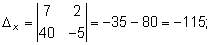
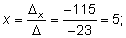
Рассмотрим систему трех уравнений с тремя неизвестными.
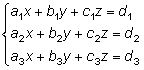(2)
Введем обозначения:
- определитель системы.
Определители Δx, Δy, Δz получаются из определителя системы Δ путем замены соответственно первого, второго и третьего столбца столбцом свободных членов d1, d2, d3.
Если определитель системы Δ ≠ 0, то существует единственное решение системы (2):
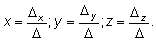
Пример. Решить систему уравнений:
Вычисляем определитель системы Δ и определители Δx , Δy , Δz разложением определителей по элементам первой строки:
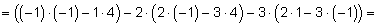
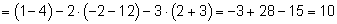
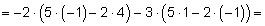
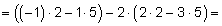
Так как Δ ≠ 0, то система имеет только одно решение:
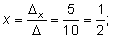
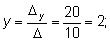
Рассмотрим применение систем в прикладных задачах.
Пример. Из двух сортов бензина образуются две смеси A и B. Смесь A содержит 60% бензина 1-го сорта и 40% 2-го сорта, смесь B содержит 80% бензина 1-го сорта и 20% 2-го сорта.
Сколько тонн смеси A и смеси B можно образовать, полностью, используя 50 тонн бензина 1-го сорта и 30 тонн бензина 2-го сорта?
Решение. Расположим все данные в таблице.
Обозначим через x1 количество тонн смеси A, через x2 количество тонн смеси B, которые можно образовать из наличного бензина, полностью его используя. На каждую тонну смеси
A идет 0,6 т (60%) бензина 1-го сорта, на x1 тонн - 0,6 x1 тонн бензина 1-го сорта. Аналогично, на x2 тонн смеси B уходит 0,8 x2 тонн бензина 1- го сорта. Следовательно, должно быть: 0,6 x1 + 0,8 x2 = 50.
Расход бензина второго сорта на смеси A и B составляет 0,4 x1 + 0,2 x2 тонн, то есть 0,4 x1 + 0,2 x2 = 30.
Итак, получили систему:
Решаем ее методом Крамера:
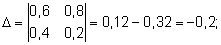
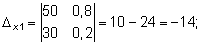
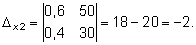
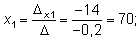
Таким образом, из 50 тонн бензина 1-го сорта и 30 тонн бензина 2-го сорта образуют 70 т смеси A и 10 т смеси B .
Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. - Электронный курс. - М: МИЭМП, 2007. -
Режим доступа к курсу: http://e-college.ru. - П. 6.4.
2.2. По формулам Крамера решить систему:
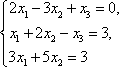
Решение: Определитель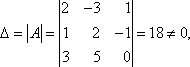
следовательно, по теореме Крамера система имеет единственное решение. Вычислим определители матриц Δ1, Δ2, Δ3, полученных из матрицы A заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
Теперь по формулам Крамера :
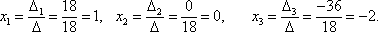
Ответ: (1; 0; –2).
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 36.
Тема 3. Ранг и базисные строки матрицы
1. Рангом матрицы A (rang А или r (А)) называется наивысший порядок отличных от нуля миноров этой матрицы.
2. Свойства ранга матрицы:
а) если матрица А имеет размеры m × n , то rang A ≤min (m; n);
б) rang A = 0 тогда и только тогда, когда все элементы матрицы А равны 0;
в) если матрица А — квадратная порядка n, то rang A = n тогда и только тогда, когда |А| ≠ 0.
3. Элементарные преобразования, не меняющие ранга матрицы:
а) отбрасывание нулевой строки (столбца);
б) умножение всех элементов строки (столбца) матрицы на число, не равное нулю;
в) изменение порядка строк (столбцов) матрицы;
г) прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
д) транспонирование матрицы.
4.С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
Ранг ступенчатой матрицы равен r .
5.Строки (столбцы) матрицы е1 , е2 , ..., еm называются линейно зависимыми, если существуют такие числа λ1 , λ2 , …, λm не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке: λ1е1 + λ2е2 + … + λmеm , где 0 = (0, 0, …, 0). В противном случае строки матрицы называются линейно независимыми.
6. Теорема о ранге матрицы:
Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов.
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 19–20.
Определение. Рангом матрицы называется число ненулевых строк в ее ступенчатом виде.
Ранг матрицы A обозначается r (A) = rang (A). Ранг матрицы не меняется при элементарных преобразованиях и не зависит от способа приведения матрицы A к ступенчатому виду.
Пример. Найти ранг матрицы:
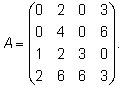
Решение системы с помощью формул Крамера
Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:
Теорема 8.22.(теорема Крамера). Если определитель матрицы, составленной из коэффициентов при неизвестных, отличен от нуля (|A| ≠ 0), то система имеет единственное решение, которое можно найти по формулам Крамера:
где D =|A| - главный определитель,
Dj - j -й вспомогательный определитель, который получен из определителя D заменой j -го столбца столбцом свободных членов.
Пример 8.20.
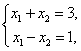
Для системы двух линейных уравнений с двумя неизвестными справедливы свойства:
-
если главный определитель равен нулю и хотя бы один их вспомогательных определителей отличен от нуля, то система решений не имеет; -
если главный определитель и оба вспомогательные определители равны нулю, то система имеет бесконечно много решений.
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. - 2-е изд., стер. - М.: КНОРУС, 2008. - С. 145–146.
Рассмотрим систему уравнений:
(1)Введем обозначения:
Если определитель системы Δ ≠ 0, то система (1) имеет единственное решение:
.Пример: решить систему уравнений:
Решение:
Составим и вычислим определители:
.Система имеет единственное решение:
Рассмотрим систему трех уравнений с тремя неизвестными.
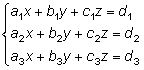(2)Введем обозначения:
- определитель системы.Определители Δx, Δy, Δz получаются из определителя системы Δ путем замены соответственно первого, второго и третьего столбца столбцом свободных членов d1, d2, d3.
Если определитель системы Δ ≠ 0, то существует единственное решение системы (2):
Пример. Решить систему уравнений:
Вычисляем определитель системы Δ и определители Δx , Δy , Δz разложением определителей по элементам первой строки:
Так как Δ ≠ 0, то система имеет только одно решение:
Рассмотрим применение систем в прикладных задачах.
Пример. Из двух сортов бензина образуются две смеси A и B. Смесь A содержит 60% бензина 1-го сорта и 40% 2-го сорта, смесь B содержит 80% бензина 1-го сорта и 20% 2-го сорта.
Сколько тонн смеси A и смеси B можно образовать, полностью, используя 50 тонн бензина 1-го сорта и 30 тонн бензина 2-го сорта?
Решение. Расположим все данные в таблице.
| Наличие бензина | Вид смеси | Процентное содержание | ||
| 1-го сорта | 2-го сорта | 1-го сорта | 2-го сорта | |
| 50 т | 30 т | А | 60% | 40% |
| | | В | 80% | 20% |
Обозначим через x1 количество тонн смеси A, через x2 количество тонн смеси B, которые можно образовать из наличного бензина, полностью его используя. На каждую тонну смеси
A идет 0,6 т (60%) бензина 1-го сорта, на x1 тонн - 0,6 x1 тонн бензина 1-го сорта. Аналогично, на x2 тонн смеси B уходит 0,8 x2 тонн бензина 1- го сорта. Следовательно, должно быть: 0,6 x1 + 0,8 x2 = 50.
Расход бензина второго сорта на смеси A и B составляет 0,4 x1 + 0,2 x2 тонн, то есть 0,4 x1 + 0,2 x2 = 30.
Итак, получили систему:
Решаем ее методом Крамера:
Таким образом, из 50 тонн бензина 1-го сорта и 30 тонн бензина 2-го сорта образуют 70 т смеси A и 10 т смеси B .
Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. - Электронный курс. - М: МИЭМП, 2007. -
Режим доступа к курсу: http://e-college.ru. - П. 6.4.
2.2. По формулам Крамера решить систему:
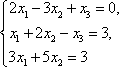
Решение: Определитель
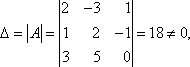следовательно, по теореме Крамера система имеет единственное решение. Вычислим определители матриц Δ1, Δ2, Δ3, полученных из матрицы A заменой соответственно первого, второго и третьего столбцов столбцом свободных членов: Теперь по формулам Крамера :
Ответ: (1; 0; –2).
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. -
2-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2007. -
(Серия «Золотой фонд российских учебников») - С. 36.
Тема 3. Ранг и базисные строки матрицы
1. Рангом матрицы A (rang А или r (А)) называется наивысший порядок отличных от нуля миноров этой матрицы.
2. Свойства ранга матрицы:
а) если матрица А имеет размеры m × n , то rang A ≤min (m; n);
б) rang A = 0 тогда и только тогда, когда все элементы матрицы А равны 0;
в) если матрица А — квадратная порядка n, то rang A = n тогда и только тогда, когда |А| ≠ 0.
3. Элементарные преобразования, не меняющие ранга матрицы:
а) отбрасывание нулевой строки (столбца);
б) умножение всех элементов строки (столбца) матрицы на число, не равное нулю;
в) изменение порядка строк (столбцов) матрицы;
г) прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
д) транспонирование матрицы.
4.С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
Ранг ступенчатой матрицы равен r .
5.Строки (столбцы) матрицы е1 , е2 , ..., еm называются линейно зависимыми, если существуют такие числа λ1 , λ2 , …, λm не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке: λ1е1 + λ2е2 + … + λmеm , где 0 = (0, 0, …, 0). В противном случае строки матрицы называются линейно независимыми.
6. Теорема о ранге матрицы:
Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов.
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 19–20.
Определение. Рангом матрицы называется число ненулевых строк в ее ступенчатом виде.
Ранг матрицы A обозначается r (A) = rang (A). Ранг матрицы не меняется при элементарных преобразованиях и не зависит от способа приведения матрицы A к ступенчатому виду.
Пример. Найти ранг матрицы: