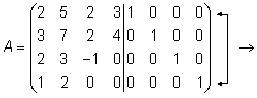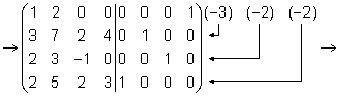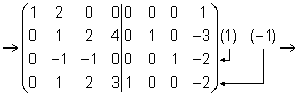ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 73
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение. Приведем матрицу A к ступенчатому виду.
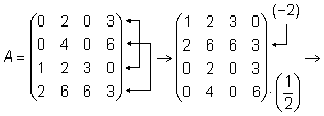
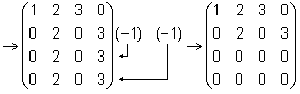
Ранг матрицы A равен двум, r (A) = rang (A). В любой матрице A с рангом r (А) = k найдутся такие k строки, что ранг матрицы, составленной их этих строк, также равен k . Такие строки матрицы A называются базисными . Если при приведении матрицы A к ступенчатому виду не использовать прибавление какой-либо строки низшей, чем данная, то базисные строки матрицы A — это в точности те строки, которые при приведении к ступенчатому виду перешли в ненулевые строки. Найдем базисные строки матрицы в последнем примере. Для этого будем отмечать ненулевые строки слева, начиная с последней матрицы (ступенчатого вида матрицы A). Затем отметим соответствующие им строки у каждой матрицы, учитывая изменение положения строк (элементарные преобразования 1-го типа). У матрицы A базисные строки 3-я и 4-я.
Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. —
Режим доступа к курсу: http://e-college.ru. — П. 6.5.
1.51. Найти ранг матрицы:
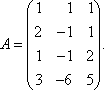
Решение. Матрица А имеет размер 4 × 3, значит, r (А) ≤ 3. С помощью элементарных преобразований, не меняющих ранг матрицы, приведем матрицу А к ступенчатому виду.
1) Транспонируем матрицу А :
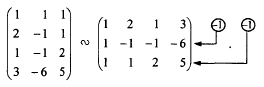
2) Умножим элементы 1-й строки на (–1), сложим ее со 2-й и 3-й строками матрицы. В новой матрице поменяем местами 2-ю и 3-ю строки:
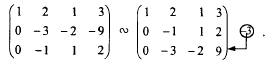
3) Умножим элементы 2-й строки на 3 и сложим с элементами 3-й строки:
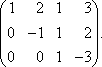
Получили ступенчатую матрицу размера 3 × 4, у которой 3 ненулевых элемента на главной диагонали, значит, r (А) = 3. Эта матрица имеет ненулевой минор 3-го порядка, например,
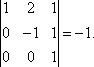
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 20–21.
Тема 4. Операции над матрицами
Определение 8.25. Транспонированием матрицы называется такое преобразование матрицы, при котором строки и столбцы меняются ролями при сохранении номеров. Транспонированная матрица обозначается АТ .
Для квадратной матрицы это преобразование эквивалентно симметричному отображению относительно главной диагонали.
Определение 8.26. Суммой (разностью) двух матриц одинакового порядка называется матрица того же порядка, каждый элемент которой равен сумме (разности) соответствующих элементов исходных матриц.
Определение 8.27. Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента исходной матрицы на это число.
Пример 8.7.
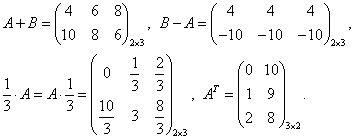
Определение 8.28. Произведением двух матриц А и В , размеры которых заданы соотношением: количество столбцов первой матрицы равно количеству строк второй, называется матрица С , у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй. Каждый элемент данной матрицы равен сумме попарных произведений элементов соответствующей строки первой матрицы и элементов соответствующего столбца второй.
Пример 8.8.
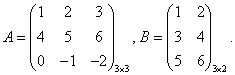
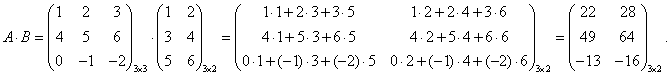
Умножить В на А нельзя, так как число столбцов матрицы В не равно числу строк матрицы А .
Пример 8.9.
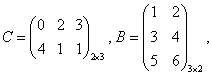
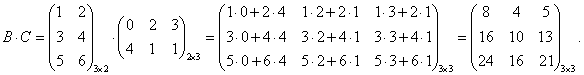
В · С ≠ С · В. Произведение матриц не коммутативно!
Пример 8.10.
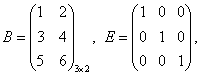
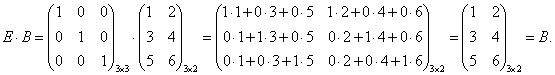
А · Е = Е · А = А
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 127–129.
5. Возведение квадратной матрицы А в целую положительную степень m (m > 1):
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 7.
Тема 5. Свойства операций над матрицами
Обратная матрица
Определение 8.33. Квадратная матрица называется вырожденной, если ее определитель равен нулю, и невырожденной - в противном случае.
Определение 8.34. Матрица 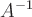 называется обратной к квадратной матрице А n -го порядка, если А × А - 1 = А - 1 × А = Е .
называется обратной к квадратной матрице А n -го порядка, если А × А - 1 = А - 1 × А = Е .
Теорема 8.15.Для любой невырожденной квадратной матрицы существует единственная обратная матрица.
Доказательство. 1 часть (единственность).
Предположим, что обратная матрица существует. Докажем, что она единственная. Предположим противное, т. е. существует две обратные матрицы: 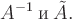
Тогда А × А - 1 = А - 1 × А = Е и 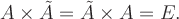
Рассмотрим равенство
А × А - 1 = Е .
Умножим его слева на 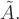
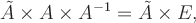
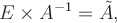
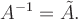
Получили противоречие.
2 часть (существование). Дана матрица
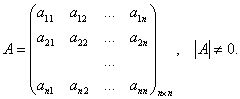
Построим обратную матрицу. Для этого совершим ряд действий:
1) заменим все элементы матрицы их алгебраическими дополнениями:
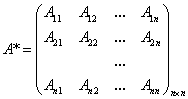 -матрица, присоединенная к матрице А ;
-матрица, присоединенная к матрице А ;
2) транспонируем полученную матрицу:
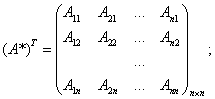
3) разделим все элементы на число |А|
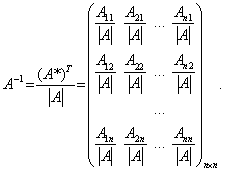
Проверим, будет ли полученная матрица обратной к исходной. Для этого умножим матрицу А на 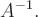 Элемент, стоящий в i -й строке и j -м столбце матрицы произведения, будет равен
Элемент, стоящий в i -й строке и j -м столбце матрицы произведения, будет равен
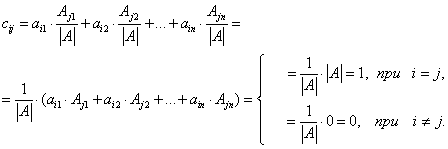
Элементы матрицы-результата совпадают с элементами единичной матрицы Е . Следовательно, А × А - 1 = Е , т. е. 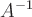 - обратная матрица к А .
- обратная матрица к А .
Таким образом, для произвольной невырожденной матрицы можно построить обратную матрицу и, следовательно, обратная матрица существует. Теорема полностью доказана.
Элементарные преобразования над матрицей.
Нахождение обратной матрицы
Определение 8.35. Элементарными преобразованиями над матрицей называются:
1) умножение любой строки на число, отличное от нуля;
2) прибавление к элементам одной строки соответствующих элементов другой, умноженных на одно и то же число;
3) перестановка строк;
4) отбрасывание строки из нулей.
Определение 8.36. Две матрицы называются эквивалентными (А
В), если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.
Теорема 8.16.Любую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице того же порядка. Применяя ту же последовательность элементарных преобразований к единичной матрице, можно получить обратную матрицу к данной.
Обычно элементарные преобразования производят над данной матрицей и единичной одновременно. Для этого составляют расширенную матрицу, в левой части которой стоит исходная матрица, а в правой -единичная матрица того же порядка. С помощью элементарных преобразований в левой части создают единичную матрицу, параллельно в правой части автоматически создается обратная матрица.
Пример 8.17. Пусть дана матрица
Составим расширенную матрицу:
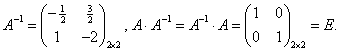
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. -2-е изд., стер. -М.: КНОРУС, 2008. -С. 134–137.
| Обратная матрица |
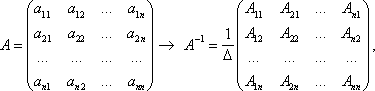 где Δ - определитель матрицы A (Δ ≠ 0) A ij - алгебраические дополнения элементов a ij матрицы А. A × A –1 = A –1 × A = E |
Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. -Ульяновск: ООО «Вектор-С», 2008. -С. 9.
Пример. Для матрицы
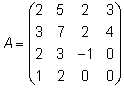 найти обратную матрицу
найти обратную матрицу Решение: