ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.03.2024
Просмотров: 42
Скачиваний: 0
СОДЕРЖАНИЕ
2) Оптимизация решений в условиях неопределенности
2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
3) Оценка операции по нескольким показателям.
4) Геометрическая интерпретация озлп.
Анализ положения l относительно одр.
Дадим геометрическую интерпретацию поиска оптимального решения.
Тогда (x1*, x2*, …, xn*) – оптимальное решение
5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
6) Симплекс-метод решения задачи лп.
7) Табличный алгоритм замены переменных.
8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.
13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
15. Решение игры в смешанных стратегиях.
Пример: определить является ли совместной система СЛУ:
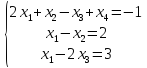
|
Матрица системы:
|
Расширенная матрица системы:
|
Выделим матрицу 3х3 и найдем определитель
|
2 |
1 |
-1 |
|
1 |
-1 |
0 |
|
1 |
0 |
-2 |
Определитель Δ = 5 (перебираем все определители матрицы системы и расширенной матрицы) они все между собой будут равны, следовательно, система совместна, т.к. rc = rp.
На самом деле r показывает число независимых линейных уравнений.
Рассмотрим следующие случаи:
1) r = n (ранг равен числу неизвестных) Система имеет единственно решение: xj = Δj / Δ
(определитель матрицы, где j-тый столбец заменили на свободные члены / обычный определитель)
Если все xj положительные, то найденное решение является допустимым и оно же является оптимальным.
Если хоть какой-то x отрицательный, то система решений не имеет.
2) r = m (ранг равен числу уравнений)
Система имеет бесконечное множество решений, т.е. совокупность значений x1, x2, …, xn, удовлетворяющий уравнениям – ограничениям.
Если среди этих решений нет ни одного, для которого все x1, x2, …, xn неотрицательны, это значит, что основная задача не имеет допустимого решения.
Если же есть какие-то решения системы, для которых все x1, x2, …, xn неотрицательны, то каждое из них допустимо.
Возникает вопрос – какое из допустимых решений будет оптимальным. Решение производится в зависимости от соотношения n и m.
|
n – m = 2 |
n – m > 2 |
|
Геометрический способ решения |
Вычислительные способы решения |
Используется прием:
1) (n-m) – количество свободных переменных, остальные переменные – базисные.
2) В области этих свободных переменных ищем ОДР.
4) Геометрическая интерпретация озлп.
Пусть имеется задача ЛП с n независимыми x1, x2, …, xn и m линейно-независимыми уравнениями, в которой n-m = 2.
Алгоритм решения:
1) Выбираем 2 свободные переменные (пусть x1 и x2).
2) Остальные переменные (базисные) выражаем через эти 2, используя метод Гаусса (последовательного исключения переменных).
3) Получаем m уравнений следующего вида:
m
штук уравнений
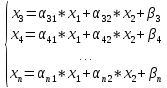
4)
В области свободных переменных (координаты
x1
и x2)
находим ОДР, для которой все базисные
переменные будут не отрицательными (хj
≥ 0, j
=
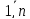 ,
т.е.работает в 1 квадранте).
,
т.е.работает в 1 квадранте).
5) Для каждой базисной переменной проделываем следующее:
x3
= 0, (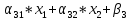 = 0), т.е. приравниваем правую часть к нулю
и строим прямые.
= 0), т.е. приравниваем правую часть к нулю
и строим прямые.
– по одну сторону соответствующая базовая переменная будет ≥ 0, эту часть и заштриховываем;
– по другую сторону соответствующая базовая переменная будет < 0.
6) Совмещаем все положительные полуплоскости и получаем ОДР.
(Как правило, ОДР представляет собой выпуклый многоугольник и стороны его ограничивают область. Всякая ОДР удовлетворяет системе ограничений (*)).
7) Для нахождения оптимального решения, необходимо построить L и проанализировать ее положение относительно ОДР.
Анализ положения l относительно одр.
Рассмотрим задачу, нахождения оптимального решения, т.е. такого, решение которого обращает функцию L в минимум.
L
=
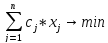 (**),
где xj
– элементы решения
(**),
где xj
– элементы решения
k = n – m = 2 (свободные переменные)
Каждая базисная переменная выражена через свободные
Если
x1
и x2
–
свободные переменные, то базисные
переменные –
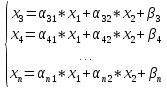
Дадим геометрическую интерпретацию поиска оптимального решения.
1) Выразим L через свободные переменные: L = γ0 + γ1*x1 + γ2*x2 (1)
Очевидно, что минимум L достигается при тех же значениях x1 и x2, что и для функции L’ = L – γ0 = γ1*x1 + γ2*x2
2) Придадим L’ некоторое постоянное значение: L’ = С.
Тогда γ1*x1 + γ2*x2 = С – уравнение прямой.
х2 = – (γ1 / γ2)* x1 + (С / γ2), т.е. угловой коэффициент = – (γ1 / γ2)
3) На самом деле, основная прямая определяется выражением L’ = 0 и проходит через начало координат. Её легко построить по двум точкам: (0;0) и (γ2; – γ1)
Положение основной прямой на плоскости Х1ОХ2 и направление уменьшения значения L’ будет зависеть от величин и знаков коэффициентов γ1 и γ2.
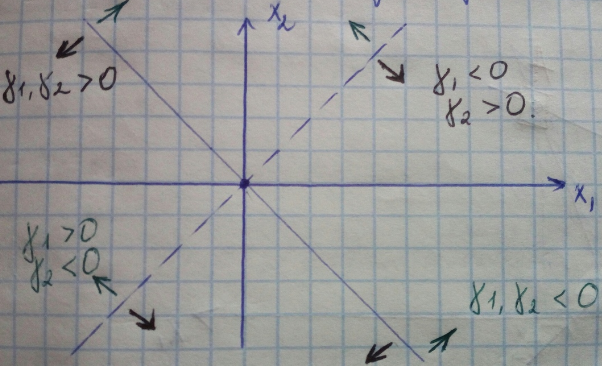
Если знаки γ1 и γ2 одинаковые, то прямая лежит во 2 и 4 квадрантах.
Зелеными стрелочками показано направление УМЕНЬШЕНИЯ L’.
(Для примера: если знаки γ1 и γ2 одинаковые (положительные), то
С = γ1*x1 + γ2*x2 и для уменьшения значения С нужно x1 и x2 уменьшать, т.е. двигать вниз)
4) Мысленно перемещаем и находим наиболее удаленную точку, в которой L’ минимальна. Эта точка должна принадлежать ОДР.
Найденная нами точка определяет оптимальное решение.
5) Опустим перпендикуляры на оси x1 и x2, таким образом найдем x1* и x2*. Подставим эти значения в выражения для базисных переменных и найдем полный набор все x3*, x4*, …, xn*
Тогда (x1*, x2*, …, xn*) – оптимальное решение
Lmin = γ0 + γ1*x1* + γ2*x2*
Пример (метода стр.13 – там условие не надо, а сразу на уравнения смотрим)
Выпишу из лекции некоторые вывода (вдруг в развернутом ответе она потребует)
Некоторые выводы
1) Решение основной задачи ЛП не может лежать внутри ОДР, а может лежать только на границе, т.к. находим экстремально удаленную точку.
2) Решение общей задачи может быть не единственным, когда оптимум достигается на всей стороне многоугольника (когда решений бесконечное множество).
3) Основная задача может не иметь решения, даже если существует ОДР. Когда ОДР не ограничена сверху (открытая область), в таком случае решения не существует.
4) Оптимальное решение всегда достигается в одной из вершин многоугольника ОДР. Решение, лежащее в одной из вершин – опорное решение, а сама вершина – опорная точка.
5) Для того, чтобы найти оптимальное решение достаточно перебрать все вершины (все опорные точки) и выбрать из них ту, в которой L минимальна.
6) Если число свободных переменных = 2, а число базисных m и решение основной задачи существует, то оно всегда достигается в одной из точек, где по крайней мере 2 из переменных обращаются в ноль.
7) Если (m<n) на 3, т.е. n-m=3, то мы приходим к случаю геометрической интерпретации в трехмерном пространстве.
Изменится: - каждое условие-ограничение не прямая, а плоскость
- ОДР если существует – выпуклый многогранник, ограничивающий часть пространства, для которой х1 ≥ 0, х2 ≥ 0, …, хn ≥ 0.
- Вместо основной прямой L’=0 имеем основную плоскость, которую также мысленно будем перемещать относительно самой себя.
Опорные точки заменяются на опорные вершины.
Такую же интерпретацию можем распространить и на n-мерное пространство.
5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
Пусть имеется задача ЛП с n переменными х1, х2, …, хn.
Ограничения имеют вид неравенств (≥0, ≤0).
Методом перестановки приводим к тому, чтобы у всех неравенств стоял знак ≥0. Тогда ограничения могут принять вид:
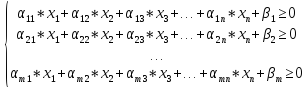 (*)
(*)
Требуется найти такие неотрицательные х1, х2, …, хn, которые удовлетворяют (*) и обращают L в минимум
[ L = C1*x1 + C2*x2 + … + Cn*xn ]
Алгоритм решения подобных задач:
1) Вводят новые переменные:

