ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.03.2024
Просмотров: 43
Скачиваний: 0
СОДЕРЖАНИЕ
2) Оптимизация решений в условиях неопределенности
2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
3) Оценка операции по нескольким показателям.
4) Геометрическая интерпретация озлп.
Анализ положения l относительно одр.
Дадим геометрическую интерпретацию поиска оптимального решения.
Тогда (x1*, x2*, …, xn*) – оптимальное решение
5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
6) Симплекс-метод решения задачи лп.
7) Табличный алгоритм замены переменных.
8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.
13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
15. Решение игры в смешанных стратегиях.
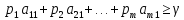
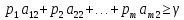
………………
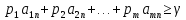 (1)
(1)
СТРОКИ ВЫШЕПЕРЕЧИСЛЕННОЙ СИСТЕМЫ ПИШЕТСЯ ПО СТОЛБЦАМ МАТРИЦЫ ИГРЫ
Разделим все получившиеся на положительную величину ???? и введем обозначения
x1 = p1/????, x2 = p2/????, …, xm = pm/????.
Тогда система (1) превращается в следующую
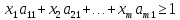
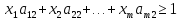
………………
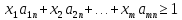 (2)
(2)
Так как р1+р2+…+pm=1, то
x1+x2+…+xm=1/????.
Мы хотим сделать наш гарантированный выигрыш максимально возможным. При этом величина 1/???? принимает минимальное значение.
Мы получаем следующую задачу линейного программирования: найти такие неотрицательные значения x1, x2, …, xm, которые удовлетворяли бы линейным ограничениям (2) и обращали бы в минимум линейную функцию
L = x1+x2+…+xm
Решив
эту задачу линейного программирования,
мы можем найти оптимальную стратегию
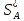 игрока А.
игрока А.
Нахождение
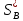 .
Оптимальная
стратегия
.
Оптимальная
стратегия
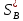 находится аналогично. Разница заключается
в том, что игрок В стремится не
максимизировать, а минимизировать
выигрыш, а значить максимизировать
величину 1/????.
Следовательно, вместо условий (2) должны
соблюдаться условия
находится аналогично. Разница заключается
в том, что игрок В стремится не
максимизировать, а минимизировать
выигрыш, а значить максимизировать
величину 1/????.
Следовательно, вместо условий (2) должны
соблюдаться условия
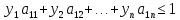
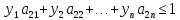
………………
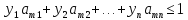 (3)
(3)
где yj = qj/ ????, j = 1, 2, …, n.
Требуется так выбрать неотрицательные значения переменных y1, y2, …, yn, чтобы они удовлетворяли условиям (3) и обращали в максимум линейную функцию
L = y1 + y2 + … + yn = 1/????
или,
что то же самое, обращали в минимум
линейную функцию
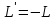
L
=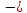 y1
y1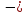 y2
y2
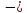 …
…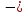 yn
=
yn
=
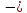 1/????
1/????
Таким образом, любая конечная игра nxm сводится к задачам линейного программирования.
Возможно, сюда еще надо будет вписать первую часть (теорию) из пункта 3.2., который идет дальше
3.2. Элементы теории статистических решений
ВОЗМОЖНО, ДЛЯ MxN
Неопределенность в данном случае, это не какой-то разумный и враждебный противник, а природа. Это незаинтересованная сторона, у нее нет сознательных действий. Такие задачи часто называются «играми с природой». Их нельзя решать методами антагонистических игр, так как со стороны «природы» противодействие отсутствует.
У стороны А имеется m возможных стратегий: А1, А2, …, Am, о природе можно сделать n предположений: S1, S2, …, Sn. Последние можно рассматривать как состояния или стратегии природы. Наш выигрыш aij при каждой паре стратегий (Ai, Sj) задается матрицей, приведенной в табл.1. Требуется выбрать такую стратегию игрока А (чистую или смешанную), которая является наиболее выгодной для него.
|
Ai |
Sj |
|||
|
S1 |
S2 |
… |
Sn |
|
|
A1 |
a11 |
a12 |
… |
a1n |
|
A2 |
a21 |
a22 |
… |
a2n |
|
… |
… |
… |
… |
… |
|
Am |
am1 |
am2 |
… |
amn |
Sj – неизвестные состояния больного организма, а стратегии Ai – возможные планы лечения. Выигрыш aij – эффективность лечения, например вероятность выздоровления. В качестве такой вероятности можно использовать соответствующую частость, либо субъективную вероятность, задаваемую экспертом.
Учитывая, что состояниями природы мы не управляем, кроме показателя aij можно ввести другие, отражающие удачность выбора данной стратегии именно в данной ситуации. К таким показателям относится риск. Риском rij игрока А при пользовании стратегии Аi в условиях Sj называется разность выигрышем, который он получил бы, если бы знал условия Sj, и выигрышем, который он получит, не зная их и выбирая стратегию Аi. Следовательно,
rij = βj – aij
При поиске оптимальной стратегии игрока А в зависимости от выбранного показателя aij или rij либо максимизируется выигрыш, либо минимизируется риск.
Так как мы хотели бы иметь наибольший выигрыш и одновременно наименьший риск, то этот объединенный показатель fij, названный «сочетанным показателем полезности», вычисляется в виде
fij = aij – rij
Чем больше fij, тем лучше, т.к. больше выигрыш и меньше риск, поэтому при оптимизации выбора Аi показатель fij нужно максимизировать.
Пусть, для примера, больной организм может находится в одном из трех состояний: S1, S2, S3 – а у врача есть три варианта лечения: А1, А2, А3. Применение лечения Аi к больному в состоянии Sj приводит к вероятности выздоровления aij. Пусть значения aij задаются матрицей Ma в виде таблицы 2.α
Таблица 2
|
Ai |
Sj |
||
|
S1 |
S2 |
S3 |
|
|
A1 |
0,95 |
0,90 |
0,85 |
|
A2 |
0,97 |
0,92 |
0,75 |
|
A3 |
0,99 |
0,75 |
0,60 |
α1=0,85
α2=0,75
α3=0,60
β1=0,99 β2=0,75 β3=0,85
Рассчитаем по этой матрице значения αi приведены справа от соответствующих строк, а значения βj – под соответствующими столбцами. Матрица Mr получается из матрицы Ma вычитанием на основе соотношения

поэтому Mr имеет виды, представленный в табл.3. Наконец матрица Mf сочетанного показателя полезности fij определяется разностью Mf = Ma – Mr и имеет вид табл.4. Для этой матрицы также рассчитаны нижняя и верхняя цена игры

При нахождении минимальных стратегий игр по полученным матрицам Ma и Mf выполняются соотношения α=β, что говорит о наличии устойчивых чистых стратегий, определяемых седловой точкой. Для обеих матриц это оказалась одной и той же 0,85. В таблицах она определяет пару оптимальных чистых стратегий (А1, S3). В общем случае решение находится в области смешанных стратегий.
Наиболее
прост для решения случай, когда заранее
известны априорные вероятности состояний:
P1=P(S1),
P2=P(S2),
…, Pn=P(Sn),
причем P1
+ P2
+ … + Pn
= 1. На практике чаще всего эти вероятности
неизвестны. Если они известны, то при
использовании показателя aij
решение игры находится на основе
максимизации среднего значения
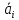 ,
где
,
где
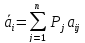
с учетом вероятностей всех возможных условий, т.е. выбираем такую стратегию Аi, для которой
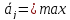
Очевидно, что при использовании показателя rij решение игры находится на основе среднего риска, т.е.
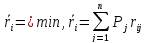
а для показателя fij
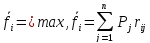
В
теории доказывается, что та же стратегия,
которая обращает в максимум средний
выигрыш
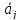 ,
обращает в минимум и средний риск
,
обращает в минимум и средний риск
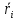 .
Там же показано, что при использовании
вероятностей состояний применение
смешанных стратегий для А не дает ему
дополнительных преимуществ, поэтому
можно обойтись чистыми стратегиями.
.
Там же показано, что при использовании
вероятностей состояний применение
смешанных стратегий для А не дает ему
дополнительных преимуществ, поэтому
можно обойтись чистыми стратегиями.

