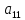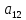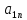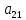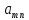Файл: Материалы по курсу (часть 1).docx

(По поводу ориентированного графа, вот его определение из интернета: Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами.

Примеры их чудесной рисовки есть в примерах, лучше если будете рисовать, взять этот, так как он прям подписан как ориент.граф)

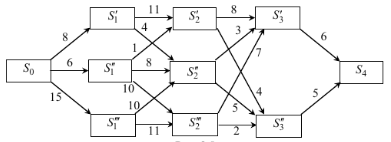
(Будьте осторожны, на картинке есть ошибка где переход от S0 к S’1, там 3 а не 8)

Далее идут два примера:

Пример 2.1. на странице 39 в печатной методе и 40 в электронной

Вот выписка из неё приведенная в конце

В рассмотренной задаче промежуточные состояния организма описывались с помощью прямоугольной сетки. В общем случае это не обязательно. Множество состояний и возможные переходы из состояния в состояние можно задать и в виде ориентированного графа. В этом случае задачи управляемого перевода организма из одного состояния в другое можно представить, как поиск кратчайшего пути на ориентированной ациклической (т. е. без петель и контуров) сети. Решаются такие задачи точно так же, как и на прямоугольной сетке. Заметим, что использованная нами для решения прямоугольная сетка также является ориентированной ациклической сетью, если на ее отрезках проставить стрелки всех возможных управлений. Ниже приведена задача, описываемая в виде сети.

Пример 2.2. на странице 42 в печатной методе и 43 в электронной

12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.

До сих пор мы рассматривали детерминированную модель (аналитическое представление закономерности, операции и т.п., при которых для данной совокупности входных значений на выходе системы может быть получен единственный результат.) динамического программирования. В реальной жизни как на состояние системы, так и на целевую функцию влияют случайные факторы, и поведение системы зависит не только от начального состояния S₀ и выбранного управления x, но и от случайности.

Рассмотрим стохастическую (т.е. случайную) модель задачи о кратчайшем пути на ациклической сети. Допустим существование в системе условных вероятностей P (S_i / S_i−1 , x_i ) того, что на i-м шаге управления система перейдет в состояние Si при условии, что до этого она находилась в S_i−1 и было применено управление x_i . Это условие представляет собой допущение о марковском свойстве системы, согласно которому вероятность перехода системы в какое-либо состояние Si зависит только от состояния S_i−1 , из которого совершается переход, и от применяемого управления x_i , но никак не зависит от предыстории системы, предшествующей ее переходу в S_i−1.

Таким образом, теперь управляющее воздействие x_i на 1-м шаге управления может лишь изменить вероятности перехода из данного состояния S_i−1 в другие состояния S_i . Теперь, находясь в каком-либо состоянии и применяя некоторое управление, можно говорить только о средних затратах 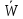времени достижения конечного состояния, которые вычисляются как взвешенные по соответствующим вероятностям затраты, рассмотренные по всем возможным из данного состояния траекториям. В этом случае, очевидно, задача заключается в нахождении такого множества оптимальных управлений (по одному для каждого состояния), которое дает минимальное среднее значение времени перехода из S₀ в S_m .

Применение принципа оптимальности к таким задачам приводит к стохастической модели динамического программирования. Пусть 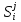обозначает конкретное состояние системы, в которое она переходит на i-м шаге, 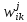– временные затраты на перевод организма в состояние 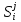на i-м шаге из состояния .

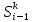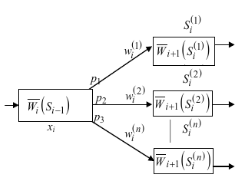
Рис. 4

Допустим, что для части сети (рис. 4) известны условные минимальные средние временные затраты 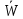_i+1 (S_i ) на достижение конечного состояния из Si (Si ∈{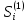 , 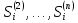}). На рис. 4 через p₁, p₂, …, p_n обозначены условные вероятности перехода

p_j = P (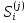 | S_i−1, x_i ), причем

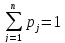
Если, например, находясь в состоянии S_i−1 , мы применяем управление x_i , то средние затраты времени 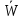_i (S_i−1 | xi ) на достижение конечного состояния из S_i−1 равны

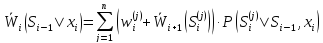
Так как вариантов управления на i-м шаге может быть несколько, т. е. xi может принимать разные значения xi ∈{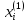 , 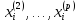}, выберем то из них, при котором 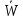_i (S_i−1|x_i) становится минимальным. При этом стохастическое обобщение основного рекуррентного уравнения (см. в предыдущем вопросе его) имеет вид

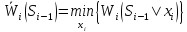
или в развернутой форме

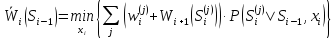
Поскольку применяются условные вероятности, то

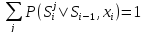
Далее следуют примеры:

Пример 2.3. на странице 48 в печатной методе и 49 в электронной

Пример 2.4. на странице 51 в печатной методе и 52 в электронной

13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.

Рассмотрим игру (модель конфликтной ситуации), в которой участвуют два игрока A и B, имеющие прямо противоположные интересы, поэтому выигрыш одного равен проигрышу другого. Такая игра называется парной игрой с нулевой суммой. Если игрок A выигрывает a, то игрок B при этом выигрывает −a, поэтому сумма выигрышей всегда равна нулю. Процесс игры заключается в последовательных ходах (личных – сознательных и случайных) противников, а совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации называется стратегией игрока. При конечном числе стратегий игра будет конечной. Пусть у игрока A имеется m возможных стратегий A₁, A₂, …, A_m, а у игрока B – n возможных стратегий B₁, B₂, …, B_n. Пусть также известны величины a_ij – выигрыши игрока A при использовании A_i с его стороны и B_j со стороны противника. Тогда игра, называемая игрой m×n, может быть представлена таблицей, называемой платежной матрицей B_j или просто матрицей игры (табл. 1).

Таблица 1

Приведение игры к матричной форме может само по себе составить трудную задачу, однако таким путем многоходовая игра фактически сводится к одноходовой – от игрока требуется сделать только один ход: выбрать подходящую стратегию. Для данного игрока среди всех стратегий имеется оптимальная, обеспечивающая ему максимальный выигрыш. Задача теории игр – нахождение оптимальных стратегий игроков в предположении одинаковой «разумности» противников.

14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.

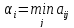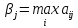По платежной матрице (см. предыдущий вопрос) игры определяется нижняя α и верхняя β цены игры. Допустим, что (выбираем минимальное число в строке, записываем их рядом и у нас получается столбец из минимальных значений), (выбираем максимальное число в столбце – строка из максимальных), тогда

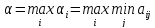(из выписанных сбоку в столбец минимальных значений ищем максимальное)

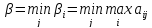(из выписанных снизу в строку максимальных значений ищем минимальное)

Принцип выбора противниками стратегий, соответствующих получению ими выигрышей α и β называется принципом минимакса, а сами стратегии – минимаксными. Минимаксные стратегии устойчивы по отношению к информации о поведении другой стороны только в случае, если α=β. Тогда у матрицы есть седловая точка (это месторасположение совпавшего числа (чистой стратегии) в матрице аля (2,3) – то есть вторая строка третий столбец). а величина ????=α=β называется ценой игры. Стратегии A_i и B_j, при которых достигается выигрыш ????, называются оптимальными чистыми стратегиями, а их совокупность – решением игры.

Возможно, еще подойдет первая часть решения задачи из пункта 3.2 (она будет в самом конце).