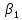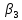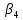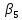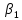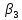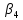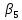ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.03.2024
Просмотров: 50
Скачиваний: 0
СОДЕРЖАНИЕ
2) Оптимизация решений в условиях неопределенности
2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
3) Оценка операции по нескольким показателям.
4) Геометрическая интерпретация озлп.
Анализ положения l относительно одр.
Дадим геометрическую интерпретацию поиска оптимального решения.
Тогда (x1*, x2*, …, xn*) – оптимальное решение
5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
6) Симплекс-метод решения задачи лп.
7) Табличный алгоритм замены переменных.
8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.
13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
15. Решение игры в смешанных стратегиях.
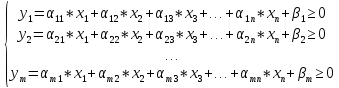 (**)
(**)
y1,
y2,
…, ym
–
добавочные переменные (также
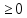 )
)
Тогда возникает новая задача ЛП – найти такие неотрицательные значения (n+m) переменных (х1, х2, …, хn) и (y1, y2, …, ym), чтобы они удовлетворяли системе (**) и обращали L в минимум.
2) Переход к классической постановке задачи.
В такой постановке (х1, х2, …, хn) рассматриваются как свободные переменные, а (y1, y2, …, ym) – базисные.
Отличия: функция L сразу выражена через свободные переменные. Если свободных переменных только 2, то используем геометрический метод, а если их больше, то используем вычислительные методы.
Пример (прикрепляю фото из лекции за 03.03)

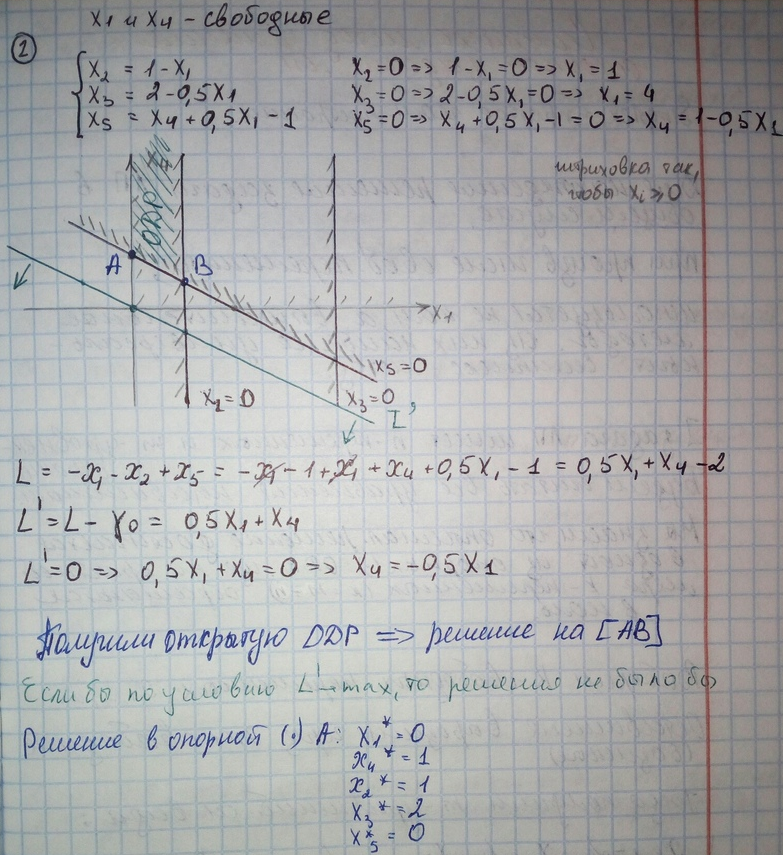
6) Симплекс-метод решения задачи лп.
Для нахождения решения задачи ЛП в общем случае при произвольном числе свободных переменных, используются не геометрические, а вычислительные методы. Из них наиболее универсальный – Симплекс-метод.
Пусть задача ЛП имеет n переменных и m уравнений-ограничений. Будем считать все уравнения независимыми. Мы знаем, что оптимальное решение достигается в одной из опорных точек ОДР, где по крайней мере k переменных (k=n-m) обращается в ноль.
Алгоритм решения:
1) Выберем k свободных переменных х1, х2, …, хk
2) Оставшиеся (базисные) выразим через эти свободные, тогда получим m уравнений следующего вида:
m
штук уравнений
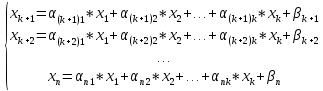
3)
Мы знаем, что опорное решение точно
достигается в точке, в которой свободные
переменные равны 0, т.е. х1
= х2
= … = хk
=
0, тогда базисные переменные будут равные
свободным членам
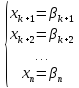 ,
такое опорное решение допустимо если
все βi
,
i
=
,
такое опорное решение допустимо если
все βi
,
i
=
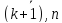 будут
будут
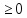 .
.
Если какое-то βi < 0, то такое решение – недопустимо и нужно искать не оптимальное, а опорное решение.
Допустим,
что все βi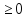 ,
тогда мы нашли опорную точку.
,
тогда мы нашли опорную точку.
4) Для того, чтобы определить оптимальное решение мы должны через свободные переменные выразить L. Тогда L = γ0 + γ1*x1 + γ2*x2 + … + γn*xn
Если
все коэффициенты при х1,
х2,
…, хk
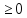 ,
то оптимум достигнут. При этом это
оптимальное решение Lmin
= γ0.
,
то оптимум достигнут. При этом это
оптимальное решение Lmin
= γ0.
Но если любой коэффициент имеет отрицательное значение, то имеет смысл соответствующую переменную сделать положительной, что позволит уменьшить значение L. Но так как опорное решение находится в точке, в которой k переменных должны быть равны 0, необходимо некоторую другую (из числа базисных) прировнять к 0.
Иными совами, нужно обменять 2 переменных: свободную и базисную.
Допустим, что γ1 < 0. Переменную x1 делаем положительной и меняем на базисную. Но из базисных переменных на обмен нужно выбрать ту, к которой:
1. Коэффициент при x1 также имеет отрицательное значение.
2. Которая быстрее всего обращается в 0 при увеличении x1.
Допустим
это строка xl
=
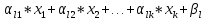 .
.
В опорном решении х2 = … = хk = 0.
Тогда,
решение в опорной точке: xl
=
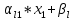 ,
нам нужно, чтобы xl
быстрее стремилось к 0, при возрастании
x1.
,
нам нужно, чтобы xl
быстрее стремилось к 0, при возрастании
x1.
Тогда,
придадим xl
= 0: x1
= –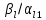 (Это
отношение свободного члена к абсолютному
коэффициенту должно быть минимальным
из всех строк)
(должно быть меньше всего для поиска
нужной строки).
(Это
отношение свободного члена к абсолютному
коэффициенту должно быть минимальным
из всех строк)
(должно быть меньше всего для поиска
нужной строки).
Искать оптимальное решение можно только если мы находимся в опорной точке.
5) Переразрешим систему уравнений-ограничений, относительно новых свободных переменных. Вместо x1 используем xl.
6) Переходим в новому опорному решению, в котором все переменные равны 0. xl становится базисной.
7) Выразим функцию L через эти новые свободные переменные:
L = γ0(1) + γ2(1)*x2 + … + γk(1)*xk + γl*xl .
Пример (прикрепляю фото из лекции за 03.03)



7) Табличный алгоритм замены переменных.
Рассмотрим СУ ограничений следующего вида:
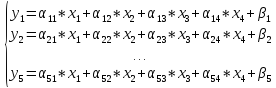
Пусть нужно вывести из свободных переменных, переменную x2 и заменить ее на базисную переменную, т.е. xj ↔ уi
Раньше бы выражали x2 через y3 и подставляли в каждое уравнение.
В пунктах ниже скобка системы не поставилась почему-то, НЕ забудьте ее поставить!
Алгоритм решения:
1) Перепишем нашу СЛ в следующем виде:
(свободный член – (остальное) )
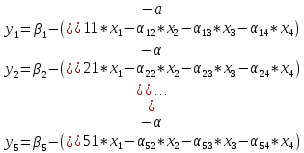
2) Введем обозначения: (-aij = αij), тогда ( минус а = альфа)
В ЭТИХ ФОРМУЛАХ ВОЗЛЕ х СТОИТ АЛЬФА!
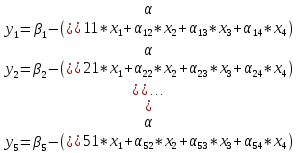
3) Представим полученную СУ в стандартной табличной форме.
|
|
Св.член |
X1 |
X2 |
X3 |
X4 |
|
Y1 |
|
α11 |
α12 |
α13 |
α14 |
|
Y2 |
|
α21 |
α22 |
α23 |
α24 |
|
Y3 |
|
α31 |
α32 |
α33 |
α34 |
|
Y4 |
|
α41 |
α42 |
α43 |
α44 |
|
Y5 |
|
α51 |
α52 |
α53 |
α54 |
4) Произведем замену переменных xj ↔ уi
Алгоритм замены хj ↔ уi:
1) Выделим разрешающий элемент αij.
Элемент xj определяет разрешающий столбец, а элемент уi разрешающую строку. На пересечении этого столбца и строки лежит разрешающий элемент.
Вычислим λ, где (λ = 1/ αij ) и запишем полученное число в нижней части разрешающей ячейки
2) Все элементы разрешающей строки (кроме αij) умножаем на λ и результат записываем в нижних частях ячеек.
3) Все элементы разрешающего столбца умножаем на (-λ) и также записываем в нижней части ячеек, также не трогая разрешающий элемент.
4) Выделяем (обводим) в разрешающей строке все верхние числа (прежние элементы), а в разрешающем столбце – нижние (новые), за исключением разрешающего элемента.
5) Для каждого из элементов, не принадлежащего ни к разрешающей строке, ни к разрешающему столбцу, запишем в нижней части произведение выделенных чисел в той же строке и в том же столбце, что и данный элемент и заполняем все ячейки.
6) Переписываем таблицу, заменяя xj ↔ уi (пусть для примера x2 ↔ у1)
|
|
Св.член |
X1 |
Y1 |
X3 |
X4 |
|
X2 |
|
\\\ |
\\\ |
\\\ |
\\\ |
|
Y2 |
|
\\\ |
\\\ |
\\\ |
\\\ |
|
Y3 |
|
\\\ |
\\\ |
\\\ |
\\\ |
|
Y4 |
|
\\\ |
\\\ |
\\\ |
\\\ |
|
Y5 |
|
\\\ |
\\\ |
\\\ |
\\\ |