ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.03.2024
Просмотров: 46
Скачиваний: 0
СОДЕРЖАНИЕ
2) Оптимизация решений в условиях неопределенности
2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
3) Оценка операции по нескольким показателям.
4) Геометрическая интерпретация озлп.
Анализ положения l относительно одр.
Дадим геометрическую интерпретацию поиска оптимального решения.
Тогда (x1*, x2*, …, xn*) – оптимальное решение
5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
6) Симплекс-метод решения задачи лп.
7) Табличный алгоритм замены переменных.
8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.
13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
15. Решение игры в смешанных стратегиях.
7) Элементы разрешающей строки и разрешающего столбца заполнить числами, стоящими в нижних частях ячеек (новыми элементами).
8) Каждый из оставшихся, заменить суммой чисел, стоящих в нижних и верхних частях ячеек.
Пример (из лекции за 10.03)
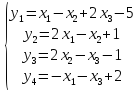
1) Перепишем систему уравнений
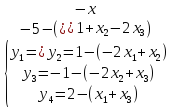
2-3) Введем обозначения (-aij = αij), и построим таблицу
|
|
Св. член |
X1 |
X2 |
X3 |
|
Y1 |
-5 |
-1 |
1 |
-2 |
|
-1/2 |
-1/2 |
-1/2 |
0 |
|
|
Y2 |
1 |
-2 |
1 |
0 |
|
-1/2 |
λ = -1/2 |
-1/2 |
0 |
|
|
Y3 |
-1 |
0 |
-2 |
1 |
|
0 |
0 |
0 |
0 |
|
|
Y4 |
2 |
1 |
0 |
1 |
|
1/2 |
1/2 |
1/2 |
0 |
4) Произведем замену переменных x1 ↔ у2
5) Выделим разрешающий элемент α21 и вычислим λ (жирными линиями показан) Элемент выделен красным
6) Все элементы разрешающей строки (кроме α21) умножаем на λ и результат записываем в нижних частях ячеек. Новые элементы выделены желтым.
7) Все элементы разрешающего столбца умножаем на (-λ) и также записываем в нижней части ячеек, также не трогая разрешающий элемент.
8) Выделяем (обводим) в разрешающей строке все верхние числа (прежние элементы), а в разрешающем столбце – нижние (новые), за исключением разрешающего элемента. Ячейки закрашены розовым цветом.
9) Для каждого из элементов, не принадлежащего ни к разрешающей строке, ни к разрешающему столбцу, запишем в нижней части произведение выделенных чисел в той же строке и в том же столбце, что и данный элемент и заполняем все ячейки.
10) Переписываем таблицу, заменяя x1 ↔ у2. Элементы разрешающей строки и разрешающего столбца заполняем числами, стоящими в нижних частях ячеек (новыми элементами). Каждый из оставшихся, заменяем суммой чисел, стоящих в нижних и верхних частях ячеек
|
|
Св. член |
Y2 |
X2 |
X3 |
|
Y1 |
-5 + (-1/2) |
|
1+(-1/2) |
-2+0 |
|
-11/2 |
-1/2 |
1/2 |
-2 |
|
|
X1 |
|
|
1 |
0 |
|
-1/2 |
-1/2 |
-1/2 |
0 |
|
|
Y3 |
-1+0 |
|
-2+0 |
1+0 |
|
-1 |
0 |
-2 |
1 |
|
|
Y4 |
2+(1/2) |
|
0+(1/2) |
1+0 |
|
5/2 |
1/2 |
1/2 |
1 |
8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
|
*общее предисловие к вопросам 8 и 9 В задаче линейного программирования (ЛП) кроме уравнений-ограничений существует ещё и линейная функция L c0 c1x1 ... cjxj ... cnxn, => нужно минимизировать. После замены xj yi её нужно выразить через новые свободные переменные x1, x2,..., xj1, yi , xj1,..., xn. Для этого можно использовать тот же алгоритм, что и для преобразования любой строки таблицы. Действительно, т.к. L c0 (1x1 ... jxj ... nxn ) , где 1 c1; 2 c2; ... n cn, мы получим её одну строку (добавочную) стандартной таблицы, в которой никогда не выбирается разрешающий элемент. С помощью табличного алгоритма обмена переменных в уравнениях основной задачи ЛП (ОЗЛП) можно решить любую задачу ЛП. Нахождение решения распадается на 2 этапа=> т.е. на 8 и 9 вопрос (отыскание опорного решения и отыскание оптимального решения). |
Отыскание опорного решения (ОР) – т.е. попутно выясняется, имеет ли вообще данная задача допустимые (неотрицательные) решения.
Пусть имеется ОЗЛП с ограничениями-равенствами, в следующей форме
y1 b1 (11x1 12x2 ...1nxn );
...
ym bm (m1x1 m2x2 ...mnxn ).
Первое пробное решение x1 x2 ... xn 0.
Если все bi 0 , то это допустимое решение. Следовательно, оно опорное.
Если какие-либо bi 0 , то это решение не допустимое и не опорное.
Для нахождения ОР нужно шаг за шагом обменивать базисные и свободные переменные пока не найдем его, либо убедимся, что система уравнений несовместима с неравенствами x1 0, x2 0,..., xn 0; y1 0, y2 0,..., ym 0.
Очевидно, нужно так обменивать базисные переменные со свободными, чтобы эта
процедура приближала нас к границе ОДР, т.е. чтобы число отрицательных свободных членов уменьшалось или при том же числе убывали их абсолютные величины.
Способ выбора разрешающего элемента для приближения к опорному решению
Пусть имеется одно из уравнений с отрицательным свободным членом.
Ищем в этой строке отрицательный ij. Если они все положительные
(значит все aij 0)), данная базисная никогда не будет положительной.
Выберем столбец, в котором находится отрицательный ij , в качестве разрешающего столбца.
Рассмотрим только те элементы столбца, которые имеют один знак со свободным членом. Выберем из них тот в качестве разрешающего элемента, для которого отношение к нему свободного члена минимально (свободный член/коэффициент при x).
Пример
Найти опорное решение задачи ЛП
y1 1 (x1 2x2 x3);
y2 5 (2x1 x2 x3);
y3 2 (x1 x2);
y4 1 (x2 x3).
|
|
Св. член
|
x1 , x1 y3
|
x2
|
x3
|
|
y1
|
1 2 |
-1 1 |
-2 1 |
1 0 |
|
y2
|
-5 4 |
-2 2 |
1 2 |
-1 0 |
|
y3 , y3 x1 |
2 2 |
1 λ=1 |
1 1 |
0 0 |
|
y4
|
1 0 |
0 0 |
-1 0 |
1 0 |
Св. член равен -5 – это плохо!
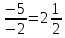 ;
- это для строки y2
;
- это для строки y2
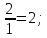 -
это для строки y3
-
это для строки y3
2<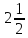 .
Производим замену y3
x1
, получаем
.
Производим замену y3
x1
, получаем
|
|
Св. член
|
y3
|
x2
|
x3, x3 y2
|
|
y1
|
3 -1 |
1 2 |
-1 3 |
1 1 |
|
y2 , y2 x3
|
-1 1 |
2 -2 |
3 -3 |
-1 λ=-1 |
|
x1 |
2 0 |
1 0 |
1 0 |
0 0 |
|
y4
|
1 -1 |
0 2 |
-1 3 |
1 1 |

