Файл: Материалы по курсу (часть 1).docx

15. Решение игры в смешанных стратегиях.

Часто α≠β, тогда для получения наибольшего выигрыша игроку выгодно не применять одну (чистую) стратегию, а чередовать случайным образом несколько стратегий. Такие стратегии, состоящие в случайном чередовании чистых стратегий, называются смешенными и задаются соответствующими вероятностными векторами. Примем, что S_A – смешанная стратегия игрока А, а S_B – смешанная стратегия игрока B. Тогда S_A = (p₁, p₂, …, p_m), S_B = (q₁, q₂, …, q_n), где p_i – вероятность применения игроком А стратегии A_i, q – вероятность применения игроком B стратегии B_j, причем

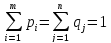
Если допустить применение смешанных стратегий (чистая стратегия – частный случай смешанной), то для каждой конечной игры можно найти хотя бы одно решение, т.е. пару устойчивых оптимальных стратегий игроков 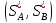, обладающих следующими свойствами: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступить от своей. Выигрыш, соответствующий решению, называется ценой игры и в общем случае (при применении смешанной стратегии) лежит в интервале α≤????≤β.

Возможно, еще подойдет вторая часть из примера из пункта 3.2 (она будет внизу).

16. Игры 2х2 и их решение.

Это самая простоя конечная игра. Ее матрица имеет вид табл. 1

Таблица 1

Если для этой матрицы α=β, то игра имеет седловую точку и ее решение – это пара чистых стратегий, пересекающихся в седловой точку. Если же в матрице 2х2 седловой точки нет и α≠β, то необходимо искать решение в смешанных стратегиях. Пара оптимальных смешанных стратегий: 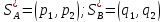, - и цена игры в этом случае определяется по формулам

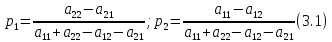
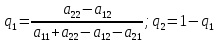
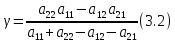
17. Геометрическая интерпретация решений игры 2х2.

Игры 2х2 имеют простую геометрическую интерпретацию. Отложим на некоторой числовой оси отрезок единичной длины А₁А₂ (рис.1). Пусть точки А₁ и А₂ соответствуют применению одноименных стратегий, а любая точка внутри этого отрезка соответствует некоторой смешанной стратегии 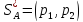. Тогда ординаты прямой В₁В₁ соответствуют выигрышу игрока А при применении им любой стратегии (чистой или смешанной) с условием, что В применяет В₁. Прямая В₂В₂ также отражает выигрыш игрока А в случае, когда В применяет В₂. Жирной линией показана граница выигрыша B1NB2 (минимальный выигрыш игрока А при любой его смешанной стратегии). Решение достигается в точке максимума нижней границы (N на рисунке). Геометрические построения легко осуществляются по элементам матрицы игры, которые откладываются на вертикальных осях. По рисунку легко находятся α, β, ???? и проводится анализ игры.

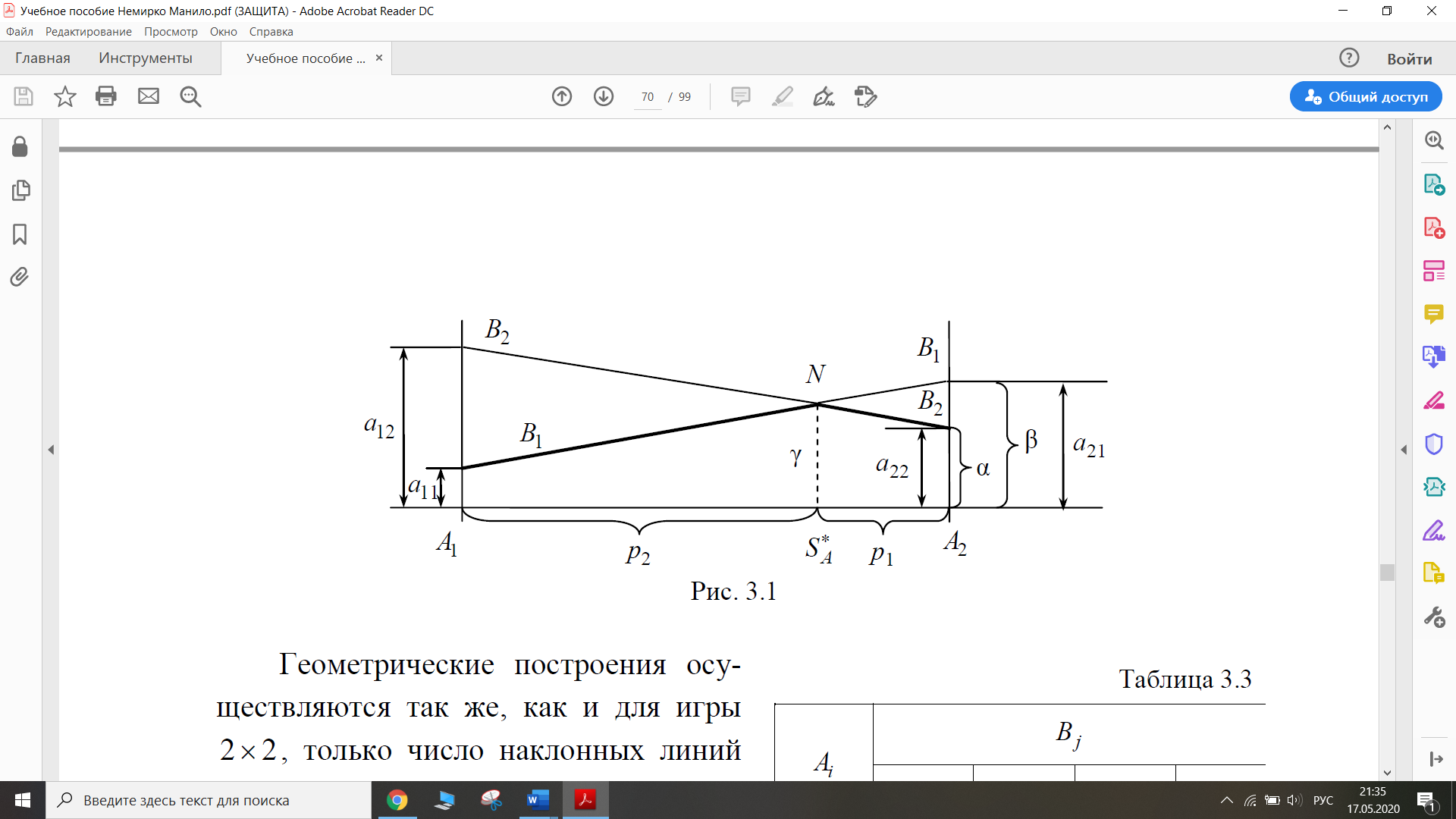
Рисунок 1

18. Решение игр 2хn.

Игры 2хn можно легко решить с помощью геометрического способа. Они задаются матрицей игры (табл.1), а на рис.1 показана геометрическая интерпретация этой игры для случая n=4.

Таблица 1

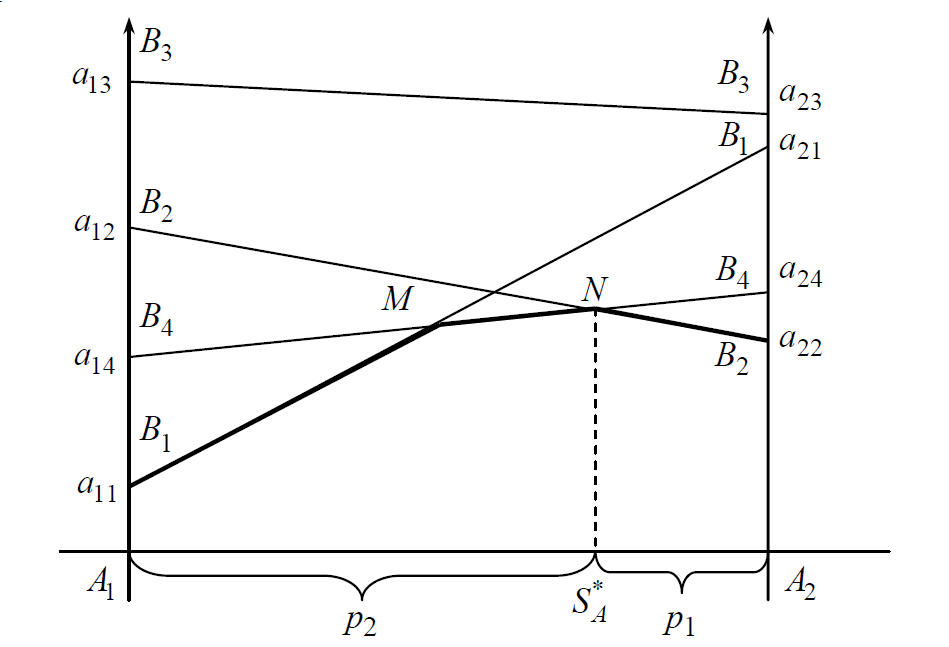
Рисунок 1

Геометрическое построение осуществляется так же, как и для игры 2х2, только число наклонных линий получается равным n, по числу стратегий для игрока В. Нижняя граница игры может быть сложной ломанной линией, максимум которой определяет решение игры.

Из рис.1 нижняя граница выигрыша B₁MNB₂, ее максимум достигается в точке N, которая определяет оптимальную стратегию 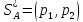. Стратегия В₃ вообще может не рассматриваться как заведомая невыгодная игроку В, а значения p₁ и p₂ можно найти по формулам игры 2х2, учитывая, что в точке N активных стратегий игрока B только две, B₂ и B₄.

Там еще ниже в след. вопросе есть алгоритм по пунктам, который можно вписать.

Пример идз Влады, любезно скинутое Тоней)

19. Решение игр mх2.

Все тоже самое пишем, как для 2xn. Но заменяем следующее

Решение игры mx2 осуществляется аналогично. Но в этом случае строится графическое изображение игры для игрока В и выделяется не нижняя, а верхняя граница выигрыша, и на ней находится точка оптимума с наименьшей ординатой (минимакс).

ОЧЕНЬ ПРИКОЛЬНАЯ ФИГНЯ МОЖНО ЗАФИГАЧИТЬ В КОНЕЦ КАК ИТОГ

ДЛЯ NX2

1. строится графическое изображение игры;

2. выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы, которая равна цене игры γ;

3. определяется пара стратегий, пересекающихся в точке оптимума M. Эти стратегии являются активными стратегиями игрока B. Если в точке оптимума пересекаются более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них;

4. решается полученная игра 2x2.

Решение игры mx2 осуществляется аналогично. Вместо пункта 2 применяется:

2. Выделяется верхняя граница выигрыша, и на ней находится точка оптимума с наименьшей ординатой.

КАК У НЕЕ В МЕТОДЕ, НО ДЛЯ НАШЕГО СЛУЧАЯ

Игры mx2 можно легко решить с помощью геометрического способа. Они задаются матрицей игры (табл.1), а на рис.1 показана геометрическая интерпретация этой игры для случая m=4.

Таблица 1

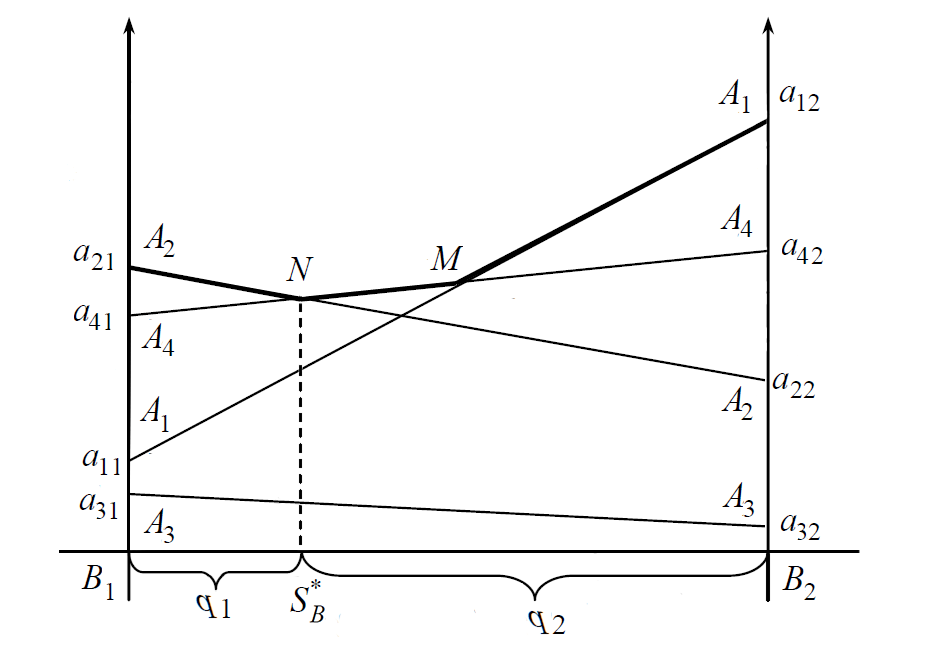
Рисунок 1

Геометрическое построение осуществляется так же, как и для игры 2х2, только число наклонных линий получается равным m, по числу стратегий для игрока A. Нижняя граница игры может быть сложной ломанной линией, максимум которой определяет решение игры.

Из рис.1 нижняя граница выигрыша А₂NMА₁, ее минимум достигается в точке N, которая определяет оптимальную стратегию 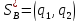. Стратегия A₃ вообще может не рассматриваться как заведомая невыгодная игроку A, а значения q₁ и q₂ можно найти по формулам игры 2х2, учитывая, что в точке N активных стратегий игрока А только две, А₂ и А₄.

20. Решение игр mxn.

Нельзя применять геометрическую интерпретацию.

Применяются чисто расчетные методы.

Решение любой игры mxn может быть сведено к задаче линейного программирования.

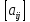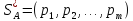Допустим у игрока А имеется m стратегий (A₁, A₂, …, A_m), у игрока B есть n стратегий: B₁, B₂, B₃. Игра задается матрицей mxn . Мы ищем две оптимальные смешанные стратегии и 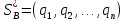, где p₁, p₂, …, p_m и q₁, q₂, …, q_n – вероятности применения соответствующих стратегий A₁, A₂, …, A_m и B₁, B₂, …, B_n и .

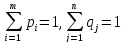Для нахождения 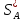полагаем, что цена игры ???? положительна (???? ≥ 0). Если есть отрицательные члены, то мы добавляем к ним достаточно большое положительное число М (также можно умножить). На решение игры это не влияет, но в конце важно не забыть провести обратные действия с ценой игры (если прибавили вычесть, если умножили разделить) – нее написано прибавить, но потом в примере (который на стр.87) вычитают, так что делаем выводы. а вообще можно написать так: Тогда цена игры увеличится на М, а вероятности останутся теми же.

Когда мы применяем 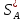, а противник – чистую стратегию Bj, то наш средний выигрыш будет равен

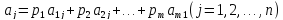
Так как мф применяем 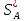, то наш средний выигрыш не может быть меньше цены игры ????, т.е. a_j>????, j = 1, 2, …, n, поэтому