ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.03.2024
Просмотров: 47
Скачиваний: 0
СОДЕРЖАНИЕ
2) Оптимизация решений в условиях неопределенности
2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
3) Оценка операции по нескольким показателям.
4) Геометрическая интерпретация озлп.
Анализ положения l относительно одр.
Дадим геометрическую интерпретацию поиска оптимального решения.
Тогда (x1*, x2*, …, xn*) – оптимальное решение
5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
6) Симплекс-метод решения задачи лп.
7) Табличный алгоритм замены переменных.
8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.
13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
15. Решение игры в смешанных стратегиях.
10. Метод динамического программирования (дп). Алгоритм решения задач управления состоянием организма в биотехнических системах. Основное рекуррентное уравнение дп.
Рассмотрим управляемый процесс, который переводит некоторую систему G из нач. состояния S0 в конеч. состояние Sm. При наличии промежуточных состояний такой перевод представляется в виде траектории, состоящей из конкретной последовательности промежуточных состояний (рис. 1). Если промежуточные состояния могут быть различными, то траектория перевода G из S0 в Sm неоднозначна и зависит от вырабатываемых управляющих воздействий x.
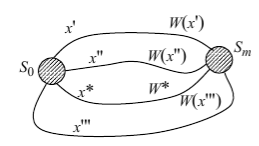
Рис.1.
Введя целевую функцию W =W(x), зависящую от выбранного управления x, можно сравнивать (по величине W) траектории друг с другом и ставить задачу об отыскании оптимальной траектории, при которой достигается экстремум W (т.е. мин или мах функции).
В зависимости от содержания целевой функции в процессе оптимизации ее стремятся либо мах-ть, либо мин-ть. Далее будет рассматриваться оптимизация, при которой W → min. Таким образом, задача заключается в отыскании оптимального управления x*, при котором целевая функция W достигает своего минимального значения W*, т. е.
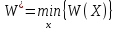 .
.
Представим себе процесс управления состоящим из конечного числа последовательных шагов. В этом случае траектория перехода G из S0 в Sm будет иметь вид последовательности промежуточных состояний S0, S1, S2, …, Sm, которая является результатом пошагового управления x, также имеющего вид последовательности x = x1, x2, …, xm.
Пусть
Si
- состояние системы G, а xi
–
управление на i-м шаге для произвольной
траектории. Для конкретной траектории
конкретное управление
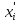 переводит G в конкретное состояние Si′.
переводит G в конкретное состояние Si′.
(!) управления x1, x2, …, xm в общем случае не числа, а векторы, функции, и т. п. (!) Пусть на каждом отдельном i-м шаге, заключающемся в переходе из Si−1 в Si, известно значение целевой функции W, которое обозначается wi . Считая выбранный критерий W аддитивным (суммирующимся), т. е. полагая, что
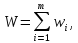
задачу оптимизации можно сформулировать следующим образом.
Требуется найти такое оптимальное управление x* = x1*, x2*, …, xm* (где xi* – оптимальное шаговое управление на i-м шаге), при котором целевая функция W принимает минимальное значение, т. е.
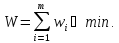
Последовательность оптимальных шаговых управлений x1*, x2*, …, xm* приводит к оптимальной траектории S0, S1*, S2*, …, Sm-1*, Sm перевода G из S0 в Sm.
Что-то вроде примера
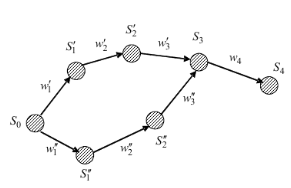
Рис.2
Для примера, приведенного на рис. 2, существуют два варианта управлений и две возможных траектории, для каждой из которых можно подсчитать значение целевой функции.
|
|
I вариант |
II вариант |
|
Управление Траектория Целевая функция |
|
|
Пусть W′ > W′′ , тогда второй вариант является оптимальным, т. е. x* = x′′, W* =W′′ .
Тут типо конец примера и важный вывод:
(!)Поиск оптимального управления x∗ методом ДП основан на использовании общего принципа, известного как принцип оптимальности:
каково бы ни было состояние S системы G в результате какого-то числа шагов, мы должны выбирать управление на ближайшем шаге так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к минимальному значению целевой функции на всех оставшихся шагах, включая данный.(!)
Схема решения (Алгоритм).
После выбора способа описания состояний управляемой системы и разбиения всего процесса управления на шаги применяется следующая процедура:
1) Перечислить набор шаговых управлений xi для каждого шага и налагаемые на них ограничения.
2)
Для каждого i-го шага определить значение
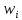 в функции от состояния Si−1
на
(i−1) -м шаге и от шагового управления xi
в функции от состояния Si−1
на
(i−1) -м шаге и от шагового управления xi
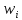 =
fi
(Si−1,
xi
) .
=
fi
(Si−1,
xi
) .
3) Определить, как изменяется состояние Si−1 системы G под влиянием управления xi на i-м шаге: оно переходит в новое состояние
Si = ϕi (Si−1, xi ) .
(не пугаемся, ϕ – это произвольная функция)
4) Пусть Wi (Si−1) – условный оптимум (наилучший вариант) целевой функции, получаемый на всех последующих шагах, начиная с i-го и до конца. Надо записать основное рекуррентное уравнение динамического программирования, выражаю-
щее Wi (Si−1)) через уже известную функцию Wi+1 (Si),
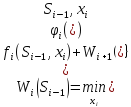
Этому условному оптимуму целевой функции соответствует условное оптимальное управление на i-м шаге xi (Si−1), которое совместно с оптимальным управлением на всех последующих шагах обращает целевую функцию на всех оставшихся шагах, начиная с данного, в минимум.
5) Произвести условную оптимизацию последнего, m-го шага, задав множество состояний Sm−1, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого Sm−1 условный оптимум целевой функции по формуле
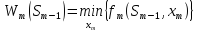
и находя условное оптимальное управление xm (Sm−1), для которого этот минимум достигается.
6) Произвести условную оптимизацию (m – 1)-го, (m – 2)-го и т. д. шагов по
формуле из п.4, полагая в ней i = (m −1), (m − 2), …, и для каждого шага указать
условное оптимальное управление xi (Si−1), при котором достигается минимум.
Так как начальное состояние системы S0 одно и оно известно, то на первом шаге варьировать состояние системы не нужно – оптимальное значение целевой функции для S0 находится непосредственно. Это и есть оптимум функции цели за весь процесс перевода:
W*=W1(S0) .
7) Произвести безусловную оптимизацию управления, учитывая выработанные ранее рекомендации на каждом шаге. На первом шаге оптимальное шаговое управление x1* = x1(S0) . Пользуясь формулой из пункта 3, находим изменившееся состояние системы S1, для него определяем оптимальное управление на втором
шаге x2*, и т. д. до конца.
11. Управление переходом организма из исходного в конечное состояние методом дп: использование ориентированного графа.
(в квадратных скобках не такая супер-важная инфа, что прям важно в них, я подчеркнула)
[Управляемый процесс перевода системы G из начального S0 - в конечное Sm -состояние можно интерпретировать как процесс лечения, который переводит организм человека из состояния «болен» в состояние «здоров», или процесс нормализации состояния человека-оператора, переводящий организм из состояния «не норма» в состояние «норма».
Если при этом реализуется возможность выделения конечного множества состояний организма, являющихся промежуточными между S0 и Sm, и можно описать шаговые управления, переводящие организм из одного состояния в другое, то для оптимизации процесса лечения или нормализации состояния можно применить метод динамического программирования.]
С помощью этого метода может быть заранее рассчитана оптимальная траектория перевода организма из S0 в Sm. В качестве критериев оптимизации, т. е. целевых функций W, могут выступать следующие: время лечения (нормализации состояния, выздоровления, вывода из опасного состояния и т. п.), токсичность применяемых медикаментов – «вредность» лечения, его стоимость, вероятность благоприятного исхода, риск осложнений и др.
[Для реальных задач предпочтительнее использовать одновременно несколько критериев, но это приводит к более сложным процедурам многокритериальной оптимизации.]
Далее в примерах мы будем использовать лишь один аддитивный критерий – время лечения или нормализации состояния.
Сформулируем задачу следующим образом. Имеется два заболевания B1 и B2, каждое из которых состоит из n последовательных стадий болезни: 1-й, 2-й, …, n -й. Стадия n – это «норма», а стадия 1 – наибольшая выраженность заболевания. За один шаг лечения посредством направленных лечебных воздействий можно изменить (увеличить) стадию только одного заболевания на 1. Условия задачи иллюстрирует рис. 2.3, где при n = 5 все возможные состояния пациента задаются узлами построенной прямоугольной сетки.
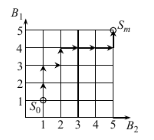
Рис.3
Для задания значений целевой функции на отрезках прямых, соединяющих узлы сетки, должны быть проставлены числа, равные времени перевода организма из состояния в состояние. Траектория перевода организма из S0 в Sm будет иметь вид ступенчатой линии. Требуется найти такую траекторию, при которой общее время лечения будет минимальным. Решение этой задачи рассмотрим в виде следующего конкретного примера.