Файл: Методические указания для проведения практических работ по профессиональному модулю Проектирование цифровых устройств.docx

Полнота системы логических функций

Полнота системы логических функций. Некоторые введенные простей­шие логические операции не являются независимыми, то есть они могут быть выражены с помощью других простейших логических операций. Эти вопросы, как и для любой алгебраической системы, относятся к проблеме так называе­мой полноты системы логических операций (функций).

Система логических функций называется полной, если все остальные ло­гические функции могут быть представлены с помощью подстановок через функции этой выбранной системы. Минимальный набор логических операций, с помощью которых можно представить логические функции, называется базисом или базисной системой. Удаление из базисной системы хотя бы одной операции нарушает свойство полноты системы операции.

Система логических функций, использующая для представления всех ло­гических функций только операции логического сложения, логического умно­жения и отрицания ( 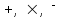) является полной, так как любая логическая функция может быть представлена с помощью операций дизъюнкции, конъюнкции и отрицания. Но такая система не является базисной, так как из нее можно исключить операцию дизъюнкции либо конъюнкции и получатся две новые системы, которые также обладают свойством полноты и уже являются

базисными. Эти два базиса так и называют — конъюнктивный базис – { 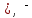} и

дизъюнктивный базис - {+, }.

Оказывается, что существуют такие единичные логические операции, кото­рые обладают свойством полноты и являются базисными, то есть с помощью одной такой логической операции можно выразить все остальные логические операции, а, следовательно, и все логические функции. Таким свойством об­ладают две элементарные бинарные логические операции: отрицание конъюнк­ции {антиконъюнкция) и отрицание дизъюнкции (антидизъюнкция), которые также часто называют по имени ученых-логиков, соответственно, штрих Шеффе­ра (|) и строка Пирса — ( 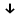). Логические операции штрих Шеффера (|) и стрелка Пирса (

---

) определяются следующим образом.

Отрицание от конъюнкции

Отрицание от конъюнкции (отрицание от логического умножения, ан­тиконъюнкция) является операцией от двух логических переменных, которая принимает нулевое значение при единичных значениях переменных. Эту логи­ческую операцию называют функцией Шеффера (штрих Шеффера) и ее обозна­чают А|В (читается: А штрих Шеффера В). Штрих Шеффера эквивалентен. А|В= =

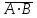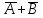
Операция штрих Шеффера – А|В задается следующей табли­цей истинности.

А	В	А|В
0	0	1
0	1	1
1	0	1
1	1	0

Отрицание от дизъюнкции

Отрицание от дизъюнкции (отрицание от логического сложения, анти­дизъюнкция) является операцией от двух логических переменных, которая при­нимает единичное значение при нулевых значениях переменных. Эту логиче­скую операцию также называется функцией Пирса (стрелка Пирса) и обознача­ют А В (читается "А стрелка Пирса В"). Стрелка Пирса эквивалентна A B=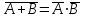

Иногда эту операцию называют НИ-НИ - "неправильно, что А и неправильно, что В"). Операция стрелка Пирса - A В задается следую­щей таблицей истинности

А	В	А В
0	0	1
0	1	0
1	0	0
1	1	0

---

Сводная таблица истинности элементарных логических операции

X	У	NOT x	х AND у	х OR у	х XOR у	х IMP y	x EQV у
0	0	1	0	0	0	1	1
0	1	1	0	1	1	1	0
1	0	0	0	1	1	0	0
1	1	0	1	1	0	1	1

Запись различных высказываний на естественном языке с помощью аппарата алгебры логики.

Аппарат математической логики можно с успехом использовать для ре­шения логических содержательных задач, отличающихся сложностью и запу­танностью исходных данных. При решении таких задач с помощью рассужде­ний паши высказывания не могут до конца выразить всю полноту мысли и не обладают достаточной ясностью. Поэтому, если предварительно перевести все высказывания в символику алгебры логики, а затем использовать аппарат этой алгебры, то можно получить четкое решение задачи с однозначным ответом. Ясно, что при решении таких задач, кроме знания самих элементарных логи­ческих операций, необходимо умение записывать высказывания, приведенные на естественном языке, с помощью символического языка алгебры логики.

Напомним еще раз» что различают два вида высказывании: простые и сложные. Простые высказывания надо рассматривать как не членимые на час­ти логические объекты. Из простых высказываний можно составить сложные высказывания. Сложное высказывание состоит из двух или более простых вы­сказываний. соединенных с помощью логических операций. Логическое зна­чение сложного высказывания зависит от истинностных значении составляю­щих его простых высказываний и его структуры.

---

Рассмотрим несколько примеров записи вы­сказываний на естественном языке с помощью аппарата алгебры логики.

Пример 1

Записать на языке алгебры логики следующее высказы­вание: "Для солнечной погоды достаточно, чтобы не было ни ветра, ни дождя".

Решение.

Введем следующие простые высказывания:

С- солнечная погода.

В - дует ветер,

D - идет дождь.

Тогда приведенное высказывание будет записано как

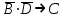
Пример 2

Записать на языке алгебры логики следующее высказывание: «Я поеду и Москву и если встречу там друзей, то мы интересно прове­дем время»

Решение.

Введем следующие простые высказывания

М - я поеду в Москву;

В - встречу там друзей;

И - интересно проведем там время.

Тогда



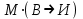
Пример 3

Записать на языке алгебры логики следующее высказывание: "Если я поеду в Москву и встречу там друзей, то мы интересно прове­дем время".

Решение.

Введем следующие простые высказывания:

М - я поеду в Москву;

В - встречу там друзей;

И - интересно проведем там время.

Тогда
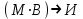
Пример 4

Записать на языке алгебры логики следующее высказы­вание: "Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя".

Решение.

Введем следующие простые высказывания:

В - дует ветер;

D - идет дождь;

С - светит солнце.

Исходное высказывание на языке алгебры логики имеет вид:



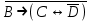
Пример 5

Записать на языке алгебры логики следующее высказывание: "Если будет солнечная погода, то ребята пойдут в лес, а если будет пасмурная погода, то ребята пойдут в кино".

Решение.

Введем следующие простые высказывания:

С - будет солнечная погона;

L - ребята пойдут в лес;

К- ребята пойдут в кино.

---

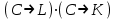
Пример 6

Записать на языке алгебры логики следующее высказы­вание: "Неверно, что если погода пасмурная, то дождь идет тогда и только то­гда, когда нет ветра".

Решение.

Введем следующие простые высказывания:

Р - будет пасмурная погода;

D - идет дождь;

В - дуст ветер.



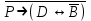
Пример 7

Записать на языке алгебры логики следующее высказы­вание: "Если не будет экономического кризиса, то достаточным условием стабильности курса рубля будет отсутствие политического кризиса в стране".

Решение.

Введем следующие высказывания:

ЕК - будет экономический кризис,

SR - будет стабильность курса рубля,

PC - будет политический кризис.

Тогда

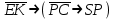
Пример 8

Записать на языке алгебры логики следующее высказы­вание: "Эффективную финансовую политику предприятия можно ожидать, ес­ли будет экономическая стабильность в обществе".

Решение.

Введем высказывания:

F- будет эффективная финансовая политика,

S - будет экономическая стабильность в обществе.

Тогда

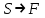
ЗАДАЧИ И УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Пусть заданы следующие два простейших высказывания: В - дует ве­тер, и D- идет дождь. Что означают на естественном языке высказывания

1.

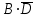
2.

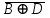
3.

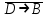
4.

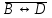
5.

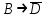
6.

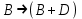
7.

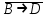
8.

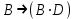
9.

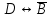
2. Переведите на язык алгебры логики следующее высказывание: "Если
для солнечной погоды необходимо отсутствие дождя, то для того, чтобы пошел
дождь, достаточно, чтобы погода была пасмурной и безветренной".

3. Переведите на язык алгебры логики следующее высказывание:
«Погода будет не только пасмурной, но и дождливой несмотря на ветер.

---