Файл: Методические указания для проведения практических работ по профессиональному модулю Проектирование цифровых устройств.docx

Алгоритм построения таблиц истинности,

Пусть задана логическая формула, и нам надо построить ее таблицу ис­тинности. Для построения таблицы истинности этой формулы необходимо выполнить следующие действия:

• 
  Определить количество переменных, входящих в формулу и составить табли­цу всевозможных значений переменных (наборов, иногда также говорят - оценок переменных), от которых зависит данная формула. Конкретные наборы можно рассматривать как числа в двоичной системе счисления и их удобно располагать в порядке возрастании от 0 до 2ⁿ -1, если количество переменных равно n.
  
• 
  Провести анализ построения этой формулы с учетом расположения скобок и приоритетности порядка выполнения логических операций. Выписать саму форму­лу, затем ее главные подформулы, затем под каждой подформулой снова выпишем главные подформулы и т.д. Количество столбцов в таблице должно быть равно сумме количества простых переменных и выделенных подформул плюс один стол­бец отводится на саму формулу. Общее количество строк должно быть на едини­цу больше, то есть 2ⁿ +1. Одна строка добавляется для записи переменных, всех подформул и самой формулы.
  
• 
  Поэтапно сверху вниз строить таблицу истинности, двигаясь слева направо, для всех подформул (лучше по порядку их выполнения). В результате получим таб­лицу истинности для исходной формулы.
  

Пример

Построить таблицу истинности для логической функции .

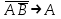Оценка	А	В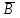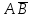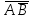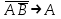
m1	0	0	1	0	1	0
m2	0	1	0	0	1	0
m3	1	0	1	1	0	1
m4	1	1	0	0	1	1

---

Отношения между формулами алгебры логики

Из полученной выше таблицы истинности видно, что истинностные значения формулы 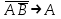точно совпадают со значением логической пере­менной А. Они либо одновременно ложны, либо одновременно истинны. Та­кие формулы называются равносильными или эквивалентными. Равносильные формулы могут содержать различное количество логических переменных. Даже в рассмотренном примере, левая часть зависит от двух логических переменных - А и В, а правая часть только от одной логической переменной А. Важно, чтобы формулы, которые называются равносильными, имели одинаковые зна­чения при одинаковых наборах логических переменных по тем переменным, от которых они зависят. Для обозначения равносильности пользуются обычно знаком равенств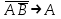а: =А

Упрощение логических формул может также проводиться но правилу подстановки. Если в формуле есть какая-либо подформула, которая равно­сильна другой формуле, то эту подформулу можно заменить равносильной. Для такой подстановки используются таблицы истинности, а на практике наи­более часто применяются законы математической логики.

С помощью таблиц истинности для формул, имеющих небольшое коли­чество переменных и число логических операций, можно достаточно просто проверить равносильность формул.

Пример

Проверить равносильность формул с помощью таблиц истинности:

1.

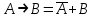
2.

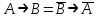
3.

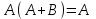
4.

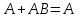
5.

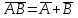
6.

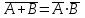
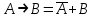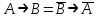А	В			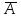		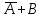А	В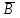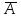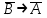
0	0	1	1	1		0	0	1	1	1	1
0	1	1	1	1		0	1	1	0	1	1
1	0	0	0	0		1	0	0	1	0	0
1	1	1	0	1		1	1	0	0	0	1

---

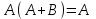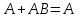А	В	А+В		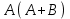	А	В	АВ	А+АВ
0	0	0	0		0	0	0	0
0	1	1	0		0	1	0	0
1	0	1	1		1	0	0	1
1	1	1	1		1	1	1	1

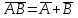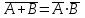А	В	АВ		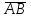		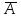		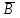		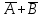А	В	А+В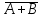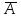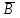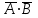
0	0	0	1	1	1	1				0	0	0	1	1	1	1
0	1	0	1	1	0	1				0	1	1	0	1	0	0
1	0	0	1	0	1	1				1	0	1	0	0	1	0
1	1	1	0	0	0	0				1	1	1	0	0	0	0

---

Таким образом, равносильными являются формулы 1 и 2, 3 и 4. Равносильные формулы можно рассматривать как "имена"' одного и то­го же объекта, то есть они взаимозаменяемы. В математике это достаточно привычная ситуация, когда некоторое математическое выражение заменяется любым ему тождественным. В простейших случаях некоторое число можно заменить другим тождественным представлением. Например, дробь 1/2 мож­но заменить на 3/6, а единицу заменить на сумму квадратов синуса и косину­са некоторого угла. Таким образом, замена одной фор­мулы на равносильную ей, ничего не меняет.

Кроме понятия равносильности формул, для определения отношения между различными формулами пользуются также такими понятиями как со­вместимость, несовместимости противоположность, логическое следование.

Две формулы называются совместимыми, если хотя бы при одной оцен­ке m_iпеременных (наборе переменных), они одновременно являются истин­ными. В противном случае они несовместимые.

Две формулы называются противоположными (инверсными), если при любой оценке переменных m_iони принимают противоположные значения и в этом случае каждая из формул является отрицанием (инверсией) другой.

Формула В называется логическим следствием формулы А, если при лю­бых оценках переменных, входящих в формулы, импликация А 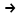В принима­ет только одно значение - истина.

Всю совокупность формул логики высказываний можно разделить на три класса:

• 
  Нейтральные или выполнимые формулы. Формулы принимают как значение 1 (истинна), так и 0 (ложно).
  
• 
  Тождественно-истинные формулы (тавтологии). Формулы принимают толь­ко значение 1 (истинно) независимо от логических значений входящих в них переменных.
  
• 
  Тождественно-ложные формулы (противоречия или контрадикции). Формулы принимают только значение 0 (ложно) независимо от логических значений входящих в них переменных.
  

Замечание. Такая же классификация справедлива и для логических функций. Все введенные определения для логических формул справедливы для логических функций и наоборот.

Тождественно-истинные и тождественно-ложные формулы называют также невыполнимыми. Тождественно-истинные и тождественно-ложные фор­мулы играют большую роль в математической логике. Эго связано с тем, что при любых наборах значений логических переменных они сохраняют постоян­ное значение истинности и, к тому же, являются взаимоинверсными. С помо­щью

---

тождественно-истинных формул, как правило, записываются основные законы математической логики.
Вариант_1__Задание_1.'>Индивидуальные задания

Вариант 1

Задание 1.

Построить таблицы истинности для логических функций.





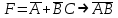
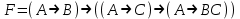
Задание 2.

Решить задачу с помощью логических операций.

Определите, кто из подозреваемых участвовал в преступле­нии, если известно:

1. 
   если Иванов не участвовал или Петров участвовал, то Сидо­ров участвовал;
   
2. 
   если Иванов не участвовал, то Сидоров не участвовал.
   

Вариант 2

Задание 1.

Построить таблицы истинности для логических функций.





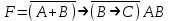
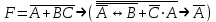
Задание 2.

Решить задачу с помощью логических операций.

Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо знавший ребят, высказал предположения:

1. 
   Аня пойдет в кино только тогда, когда пойдут Вика и Сер­гей;
   
2. 
   Аня и Сергей пойдут в кино вместе или же оба останутся дома;
   
3. 
   чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика.
   

Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались толь­ко два. Кто из ребят пошел в кино?
Вариант3

Задание 1.





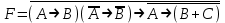
Задание 2.

Решить задачу с помощью логических операций.

На вопрос, какая завтра будет погода, синоптик ответил:

1. 
   «если не будет ветра, то будет пасмурная погода без дождя»;
   
2. 
   «если будет дождь, то будет пасмурно и без ветра»;
   

1. 
   «если будет пасмурная погода, то будет дождь и не будет ветра».
   

Подумав немного, синоптик уточнил, что его три высказыва­ния можно лаконично записать в виде одного составного вы­сказывания. Сформулируйте его.
Вариант 4

Задание 1.

Построить таблицы истинности для логических функций.

---