Файл: Методические указания для проведения практических работ по профессиональному модулю Проектирование цифровых устройств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 135
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Вариант 6.
Задание 1.
Записать числа в двоичной системе счисления: 216,275(8); 3362,1525(8).
Задание 2.
Записать числа в восьмеричной системе счисления:
1011000011,10101(2); 100010111,111001 (2)
Задание 3.
Записать числа в двоичной системе счисления: 712,375(16); 189D,F37(16).
Задание 4.
Записать числа в шестнадцатеричной системе счисления:
1010111011,11011011101112, 1000110110011,010110012
Задание 5.
Выполнить действия
| 1000010100(2) + 1101010101(2) 1011001010(2) + 101011010(2) 1110111000,101(2) + 1101100011,101(2) 1430,2(8) + 666,3(8) 388,3(16) + 209,4(16) | 1111100010(2) - 101011101(2) 1011000100(2) – 1000100000(2) 1101111000,1001(2) - 1000000,01(2) 1040,2(8) - 533,2(8) 3FВ,4(16) - 140,6(16) |
| 11111(2) 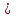 10001(2) 10001(2)1237,3(8) 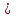 117,5{8) 117,5{8)66,4(16)- 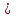 65,8(16) 65,8(16) | 1111100010(2) / 101011101(2) 1011000100(2) / 1000100000(2) 1101111000,1001(2) / 1000000,01(2) |
| | |
Вариант 7.
Задание 1.
Записать числа в двоичной системе счисления: 614,123(8); 485,92(8).
Задание 2.
Записать числа в восьмеричной системе счисления:
11100111001,01(2) 11100010000,001(2)
Задание 3.
Записать числа в двоичной системе счисления: 14А1,15(16); 190E,F7(16).
Задание 4.
Записать числа в шестнадцатеричной системе счисления:
101000011111,110110001112, 10001111100011,0100012
Задание 5.
Выполнить действия
| 1000010100(2) + 1101010101(2) 1011001010(2) + 101011010(2) 1110111000,101(2) + 1101100011,101(2) 1430,2(8) + 666,3(8) 388,3(16) + 209,4(16) | 1111100010(2) – 101011101(2) 1011000100(2) – 1000100000(2) 1101111000,1001(2) - 1000000,01(2) 1040,2(8) - 533,2(8) 3FВ,4(16) - 140,6(16) |
| 11111(2) 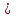 10001 (2) 10001 (2)12373(8) 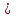 -117,5(8) -117,5(8)66,4(16) -65,8(16) | 1111100010(2) / 101011101(2) 1011000100(2) / 1000100000(2) 1101111000,1001(2) / 1000000,01(2) |
Вариант 8.
Задание 1.
Записать числа в двоичной системе счисления: 772,275(8); 3512,325(8).
Задание 2.
Записать числа в восьмеричной системе счисления:
1101011000011,10101(2); 111010111,111001 (2)
Задание 3.
Записать числа в двоичной системе счисления: 212,8375(16); 1829D,F137(16).
Задание 4.
Записать числа в шестнадцатеричной системе счисления:
1010101010111011,11011111011101112, 11010000110110011,01011110012
Задание 5.
Выполнить действия
| 11111010(2) + 10000001011(2) 1011010(2) +1001111001(2) 10110110,01(2) + 1001001011,01(2) 1706,34(8) + 650,3(8) 180,4(16) + 3А6,28(16). | 111101101(2) – 101111010(2) 1000110100(2) - 100100111(2) 1111111011,01(2) - 100000100,011(2) 1300,44(8) - 1045,34(8); 16А,8(16) - 147,6(16) |
| 100111(2) 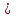 110101(2) 110101(2)1542,2(8) 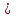 50,6(8) 50,6(8) А,8(16) 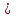 Е,2(16). Е,2(16). | 111101101(2) / 101111010(2) 1000110100(2) / 100100111(2) 1111111011,01(2) / 100000100,011(2) |
Практическая работа № 3
Тема: «Арифметические действия над числами с фиксированной точкой (сложение, вычитание)».
Цель: Изучить методику представления чисел в машинных кодах и получить практические навыки выполнения арифметических операций над числами с фиксированной точкой.
Теоретическая часть
Кодирование и обработка чисел
-
Прямой, обратный и дополнительные коды чисел
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.
Пример 1.
| A10=+10 A2=+1010 [A2]П=0:1010; | B10= -15 B2= -1111 [B2]П=1:1111. |
Точечной вертикальной линией здесь отмечена условная граница, отделяющая знаковый разряд от значащих.
Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы - нулями.
Пример 2.
| A10=+5 A2=+101 [A2]П=[A2]OK=0:101; | B10= -13 B2= - 1101 [B2]OK=1:0010. |
Свое название обратный код чисел получил потому, что коды цифр отрицательного числа заменены на инверсные. Укажем наиболее важные свойства обратного кода чисел:
-
сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕок= 1: 111... 11, состоящую из единиц в знаковом и значащих разрядах числа; -
нуль в обратном коде имеет двоякое значение. Он может быть положительным - 0: 00...0 и отрицательным числом - 1; 11... 11. Значение отрицательного нуля совпадает с МЕок. Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (2° - для целых чисел, 2-k - для дробных).
Пример 3.
| A10=+19 A2=+10011 [A2]П=[A2]OK=[A2]ДК=0:10011; | B10=- 13 В2= -1101 [B2]ДК=[B2]OK+20=1:0010 + 1 =1:0011. |
Укажем основные свойства дополнительного кода:
-
сложение дополнительных кодов положительного числа С с его отрицательным значением дает так называемую машинную единицу дополнительного кода:
МЕДК=МЕОК+20=10: 00…00,
т.е. число 10 (два) в знаковых разрядах числа;
-
дополнительный код получил такое свое название потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк.
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак “+” в этих кодах кодируется двумя нулевыми знаковыми разрядами, а “-” - двумя единичными разрядами.
Пример 4.
| A10=9 A2=+1001 [A2]П=[A2]OK=[A2]ДК=0:1001 [A2]МОК=[A2]МДК=00:1001; | B10= -9 B2= -1001 [B2]OK=1:0110 [B2]ДК=1:0111 [B2]МОК=11:0110 [B2]МДК=11:0111. |
Целью введения модифицированных кодов являются фиксация и обнаружение случаев получения неправильного результата, когда значение результата превышает максимально возможный результат в отведенной разрядной сетке машины. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов “01” свидетельствует о положительном переполнении разрядной сетки, а “10” - об отрицательном переполнении. В настоящее время практически во всех моделях ЭВМ роль удвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда.
Арифметические операции над числами с фиксированной точкой
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа A=>O и В=>О, тогда операция алгебраического сложения выполняется в соответствии с табл. 2.3.
Таблица 2.3
Таблица преобразования кодов при алгебраическом сложении
| Требуемая операция | Необходимое преобразование |
| А+В А-В -А+В -А-В | А+В А+(-В) (-А)+В (-А)+(-В) |
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с табл. 2.2. При выполнении сложения цифр необходимо соблюдать следующие правила.
-
Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа. -
Знаковые разряды чисел участвуют в сложении так же, как и значащие. -
Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу. -
При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 4. Сложить два числа А10=7 В10=16
A2=+11=+0111;
B2=+1000=+10000.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
[A2]П=[A2]OK=[A2]ДК=0: 00111;
[B2]П=[B2]OK=[B2]ДК= 0: 10000.
Сложение в обратном или дополнительном коде дает один и тот же результат