Файл: Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика.doc

Рис.3.8

Н а рис.3.9 изображен ползун, входящий в кинематические пары с шатуном и стойкой. Сила давления шатуна на ползун, разложена на составляющие и . Касательная составляющая обеспечивает перемещение ползуна вдоль стойки и совершает положительную работу, т.е. является полезной движущей силой. Нормальная составляющая , направленная перпендикулярно, работу по перемещению ползуна не совершает. Напротив, именно эта сила нормального давления определяет величину силы трения между ползуном и стойкой.
Действительно, из условия равновесия сил в направлении нормали к направляющей получаем нормальную реакцию стойки = - . Далее, на основании закона Кулона, имеем . А отсюда следует, что с увеличением возрастает , а вместе с ней и .

Следует иметь ввиду, что угол давления - не постоянная величина, а изменяется в зависимости от положений механизма.
Угол давления можно уменьшить, если увеличить размеры соответствующих звеньев механизма. При этом габаритные размеры самого механизма увеличиваются, что не всегда приемлемо.
Таким образом, оптимальным вариантом метрического синтеза является тот, когда угол давления в наиболее неблагоприятных положениях механизма достигает максимально допустимого значения, но не превышает его. При создании новых механизмов максимальный угол давления в паре шатун-ползун рекомендуется принимать равным 

---

_max = 3040.
Покажем на примере, как определяется длина звена по критерию «угол давления».

Пример.
Н а рис.3.10 изображен кривошипно-ползунный механизм с направляющей, смещенной относительно центра вращения кривошипа на величину эксцентриситета - е^*. Заданы длина кривошипа ОА и максимальный угол давления в паре шатун-ползун - _max.
Дано: ОА= r, _max, е^*.
Определить: длину шатуна  , из условия, что при полном обороте кривошипа угол давления  не превысит _max.
Решение.
Рассмотрим изменение угла давления в паре шатун-ползун при прямом и обратном движении ползуна. На рисунке сделаны обозначения:

- угол давления при прямом ходе;

- угол давления при обратном ходе.
Из геометрии следует:
(3.12) (3.13)

Анализируя (3.12) и (3.13) , находим положения механизма, при которых значения углов давления максимальны:
и при (т.е. ОА - вертикально).

Значит:

(3.14) (3.15)
Учитывая, что принимаем
Поэтому окончательно: (3.16)

6. 
   Критерий отношения средних скоростей ведомого звена
   

Иногда при проектировании механизмов бывает важно, чтобы выходное звено на рабочем и на холостом ходу двигалось с различными средними скоростями.¹ В этом случае метрический синтез механизма выполняется с учетом коэффициента отношения средних скоростей.

---

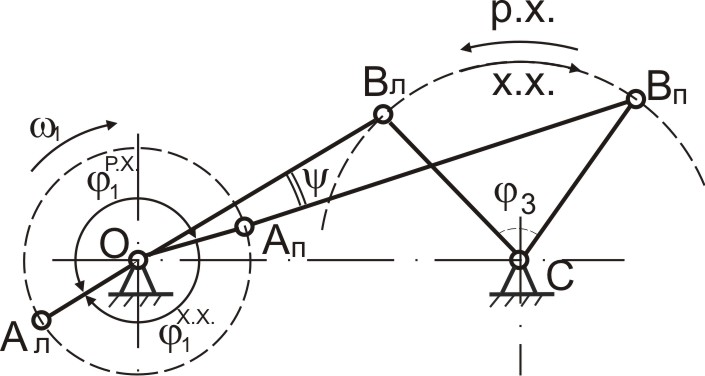Рассмотрим работу кривошипно-коромыслового механизма (рис. 3.11).

Стрелками на рисунке обозначены:
р.х.– рабочий ход ведомого звена (совершается полезная работа);
х.х. – холостой ход (полезная работа не совершается).
Предположим, что ведущее звено ОА вращается равномерно (₁=const).
Рис.3.11
Из рис. 3.11 видно, что , т.е.
Коэффициент отношения средних скоростей ведомого звена:

(для реальных механизмов, типа конвейеров  = 1.1 …1.3)

. Это следует из соотношения

Для ведущего звена

Отсюда



Имея требуемое значение , находят угол , после чего на основании рис.3.11 определяют необходимые длины звеньев.

7. 
   Метрический синтез сложного механизма
   

Сложным механизмом условно будем называть механизм, в состав которого входят несколько структурных групп.

Пример такого механизма показан на рис.3.12. Структурно он состоит из первичного механизма и двух последовательно присоединенных к нему структурных групп.

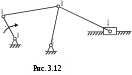Как и в случае простых механизмов, метрический синтез сложного механизма осуществляется с использованием рассмотренных выше или иных критериев. При этом вначале сложный механизм разбивается на более простые механизмы в соответствии с формулой строения. В нашем случае это механизмы ОАВС и СВД.
Метрический синтез сложного механизма выполняют в последовательности:

1. 
   синтез первого простого механизма;
   
2. 
   синтез второго простого механизма;
   
3. 
   и т.д.
   

Для закрепления изложенного материала

---

, рассмотрим последовательность операций по метрическому синтезу механизма качающегося конвейера из курсового проекта по ТММ. Предположим, что принципиальная схема механизма задана и изображена на рис.3.13.
Решение:

1. 
   Выделяем простые механизмы: ОАВС и СДЕ.
   
2. 
   Используем критерий положений коромысла СВ.
   

Дано: .

3. 
   Используем критерий положений ползуна Е.
   

Дано: .

4. 
   Критерий максимального угла давления в кинематической паре Е - .
   

Дано: .

5. 
   Критерий отношения средних скоростей выходного звена
   

Дано: крайние положения механизма, угол

 направление вращения ведущего звена.
Вопросы для самоконтроля

1. 
   Какие механизмы в ТММ называют плоскими?
   
2. 
   Нарисуйте несколько принципиальных схем плоских механизмов. Покажите низшие и высшие кинематические пары, использованные в них.
   
3. 
   Укажите достоинства и недостатки низших и высших кинематических пар.
   
4. 
   Объясните смысл задачи структурного синтеза механизма. Что при этом задается, а что подлежит определению?
   
5. 
   Объясните смысл задачи метрического синтеза механизма. Что при этом задается, а что подлежит определению?
   

Лекция 4

---

кинематический анализ плоских рычажных механизмов (графический метод)

1. 
   Основная задача и цели кинематического анализа. Методы решения. ([1], §14, п.1; §15, п.1; [2], §3.2; [3], Глава 2, §4)
   
2. 
   Определение положений механизма. ([1], §17; [2], §3.2; [3], Глава 2, §4)
   
3. 
   Определение скоростей точек и угловых скоростей звеньев механизма. ([1], §18; [2], §3.2; [3], Глава 2, §4)
   
4. 
   Определение ускорений точек и угловых ускорений звеньев механизма. ([1], §18; [2], §3.2; [3], Глава 2, §4)
   
5. 
   Кинематический анализ сложных механизмов ([3], Глава 2, §4).
   

1. 
   Основная задача и цели кинематического анализа. Методы решения.
   

Основная задача кинематики механизмов – изучение движения точек и звеньев механизма без учета сил, действующих на этот механизм.
Кинематическое исследование механизма преследует три основных цели:

1. 
   Изучение положений механизма. Изучение перемещений точек и углов поворота звеньев (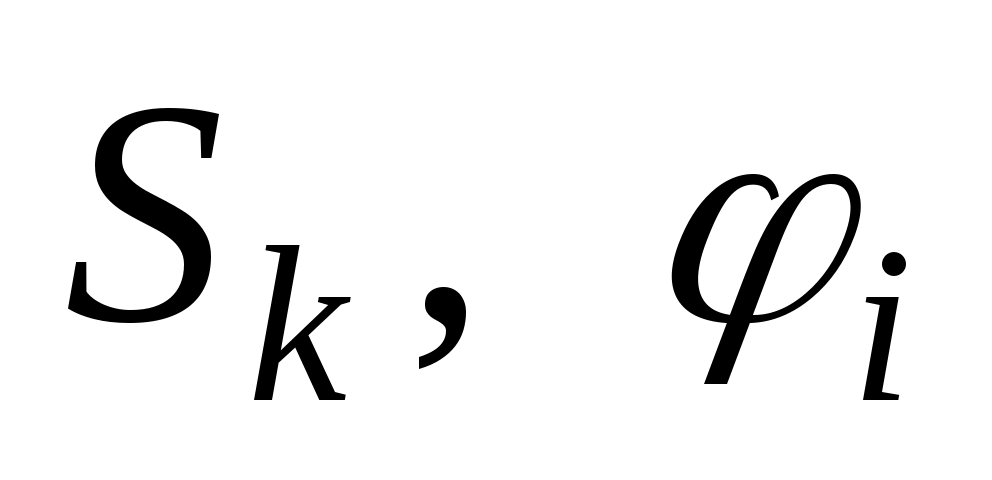 ). Определение траекторий движения точек.
   

• 
  Результаты исследований по данному пункту используются при определении габаритных размеров механизма, определении формы и размеров внутрикорпусного пространства, определения скоростей, ускорений, решении задач динамического синтеза и анализа.
  

2. 
   Определение скоростей точек и угловых скоростей звеньев ( ).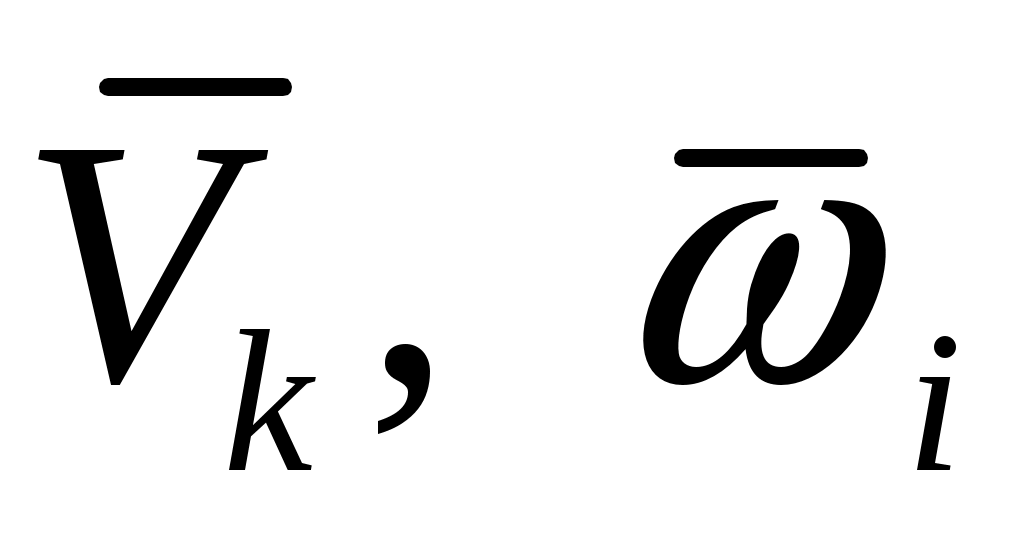
   

• 
  Найденные линейные скорости могут быть использованы, в том числе, для определения мощностей сил и приведенной силы; угловые скорости – для определения нормальных ускорений точек, мощностей моментов сил и др. целей.
  

2. 
   Определение ускорений точек и угловых ускорений звеньев ( ).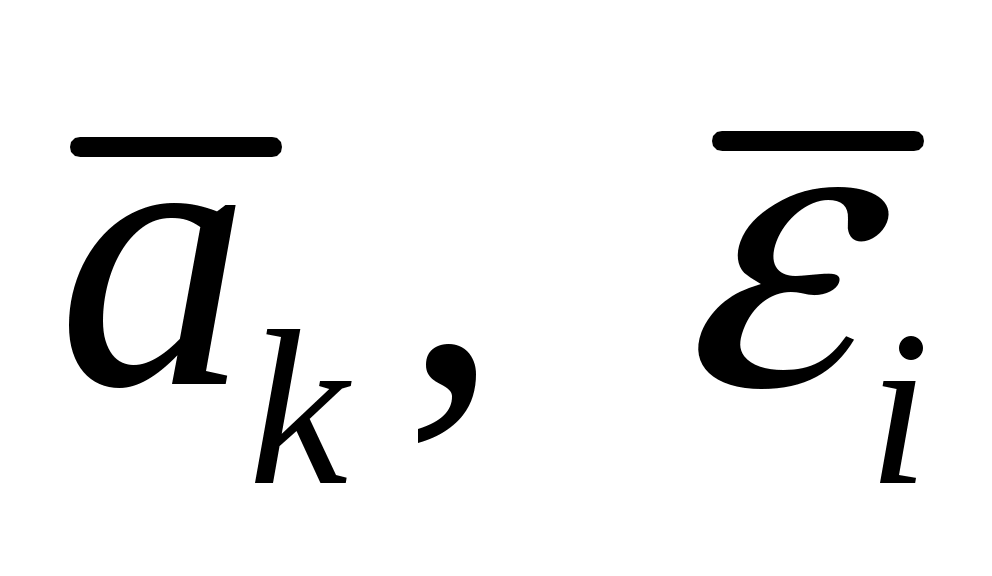
   

• 
  Ускорения в задачах динамики позволяют выполнить силовой расчет механизма, т.е. расчет движущей силы и нагруженности кинетических пар по методу кинетостатики (с использованием принципа Даламбера). В кулачковых механизмах по ускорениям судят о динамических нагрузках, возникающих в процессе работы механизма.
  

Методы кинематического анализа.

1. 
   Графический (преимущества - наглядность, прогнозируемость результатов; недостатки - низкая точность, трудоемкость).
   
2. 
   Аналитический (высокая точность, но отсутствие наглядности, необходимость дополнительной работы по составлению и отладке программы).
   

---