Файл: Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 101
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
:
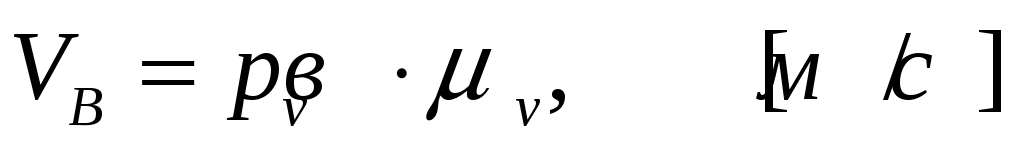
Базовый план скоростей построен.
Переходим к определению скоростей других точек. Такой точкой по условию задачи является точка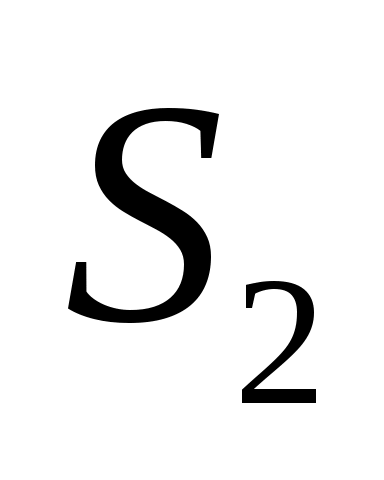 - центр масс звена 2.
- центр масс звена 2.
Скорость т.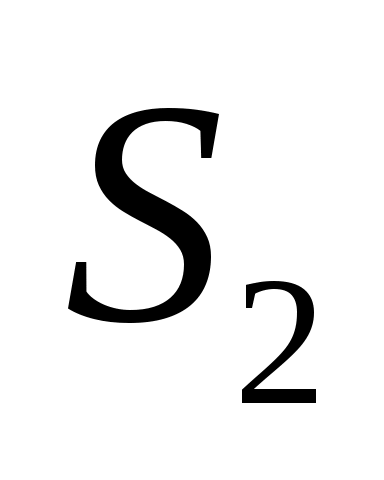 находим по аналогичной векторной формуле. В этом случае система уравнений не понадобится, т.к. вектор
находим по аналогичной векторной формуле. В этом случае система уравнений не понадобится, т.к. вектор  определен ранее, а величина и направление
определен ранее, а величина и направление  легко определяется (на основании известного
легко определяется (на основании известного  ).
).
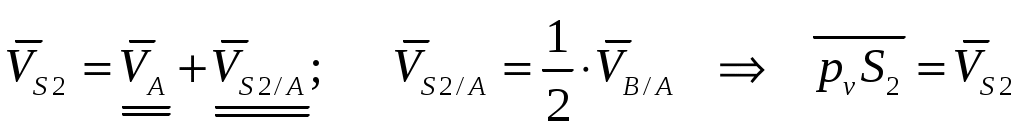 (4.4)
(4.4)
Угловые скорости и
и  найдем по формулам:
найдем по формулам:
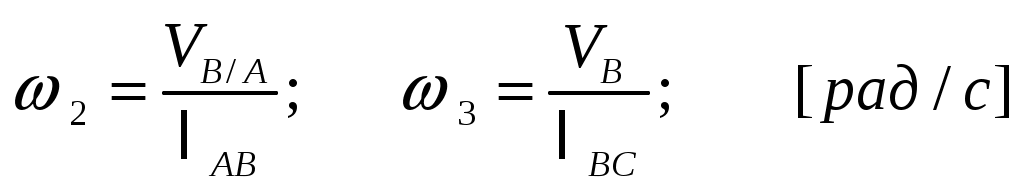 (4.5)
(4.5)
Направления и
и  изображаем на рис.4.3 в соответствии с направлениями
изображаем на рис.4.3 в соответствии с направлениями 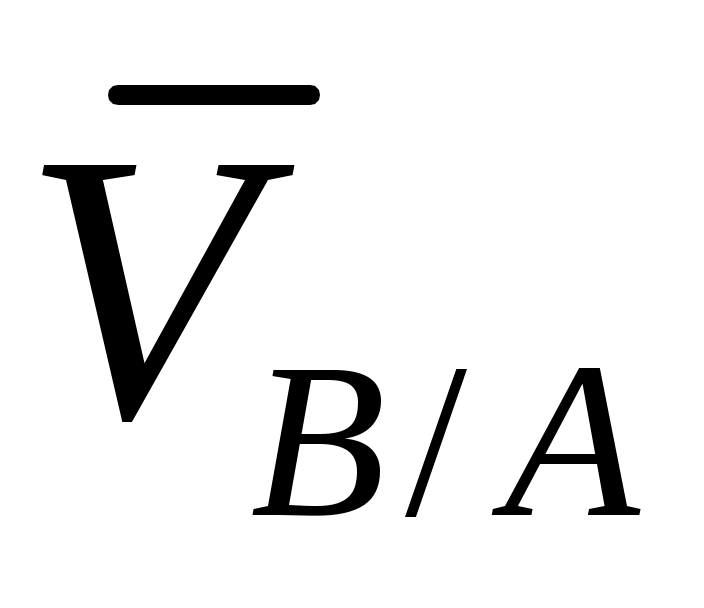 и
и  на плане скоростей.
на плане скоростей.
Пример 2.
Дано:
кривошипно-ползунный механизм (Рис.4.5) в заданном положении;
звено 1 – входное; 1 - угловая скорость звена 1; AS2 = 0,5 · AB.
Определить:
скорости точек А, В, S2 путем построения плана скоростей.
Решение
Последовательность и логика построений в данной задаче и в Примере 1 являются аналогичными. Поэтому, решение приводим в конспективном виде.
Пример 3.
Дано:
кривошипно-ползунный механизм с промежуточной кулисой (Рис.4.7) в заданном положении; звено 1 – входное; 1 - угловая скорость звена 1;
ВS4 = 0,5 · BD.
Определить:
скорости точек A, B, D, S4 путем построения плана скоростей.
Решение.
Ряд пунктов приведенного ниже алгоритма выполняются аналогично предыдущим примерам и не требуют пояснений. Затруднения могут возникнуть при определении скоростей точек структурной группы (2,3), звенья которой образуют между собой поступательную пару. Построение плана скоростей в этом случае имеет свои особенности, на которые следует обратить внимание (см. пп.2-3 алгоритма).
При построении планов скоростей кулисных механизмов характерным является использование уравнений, связывающих скорости двух точек, совпадающих в данном положении, но принадлежащих разным звеньям поступательной пары. В нашем примере таким точками будут точки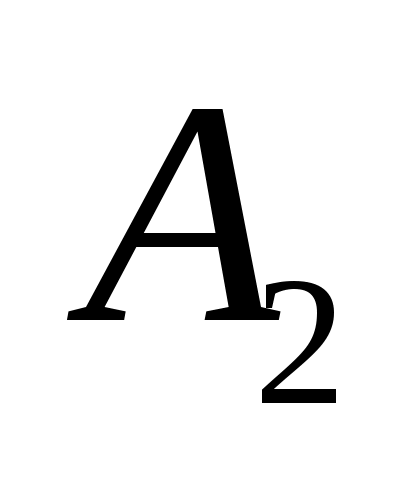 и
и 
(Рис.4.7). Точки и
и  совпадают с центром вращательной пары, соединяющей звенья 1 и 2. Поэтому
совпадают с центром вращательной пары, соединяющей звенья 1 и 2. Поэтому 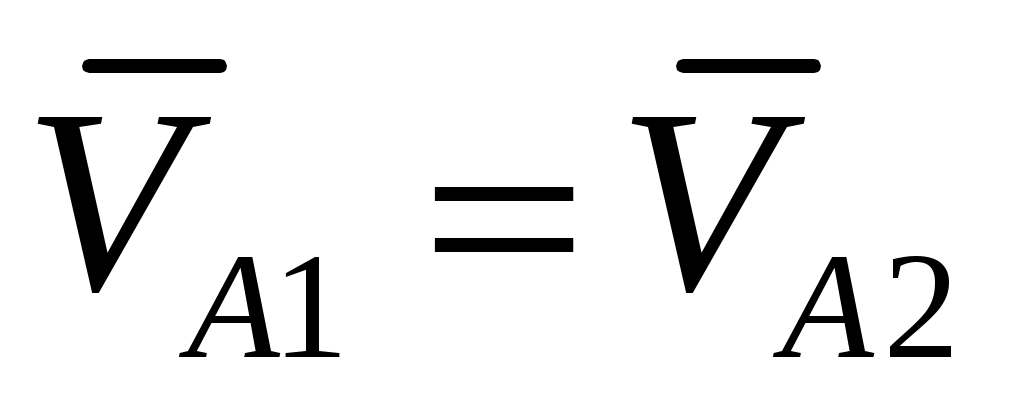 . Точка
. Точка  в данный момент совпадает по положению с точками
в данный момент совпадает по положению с точками  и
и  , но принадлежит звену 3.
, но принадлежит звену 3.
Рассматривая движение звена 2 как сложное, представим его в виде суммы двух движений: переносного вращательного со звеном 3 и относительного поступательного вдоль звена 3.
Тогда, для точки звена 2 получим векторное уравнение:
звена 2 получим векторное уравнение:
 , (4.6)
, (4.6)
где - абсолютная скорость т.
- абсолютная скорость т. ;
;
 - переносная скорость т.
- переносная скорость т. , в данный момент совпадающая со скоростью т.
, в данный момент совпадающая со скоростью т. звена 3;
звена 3;
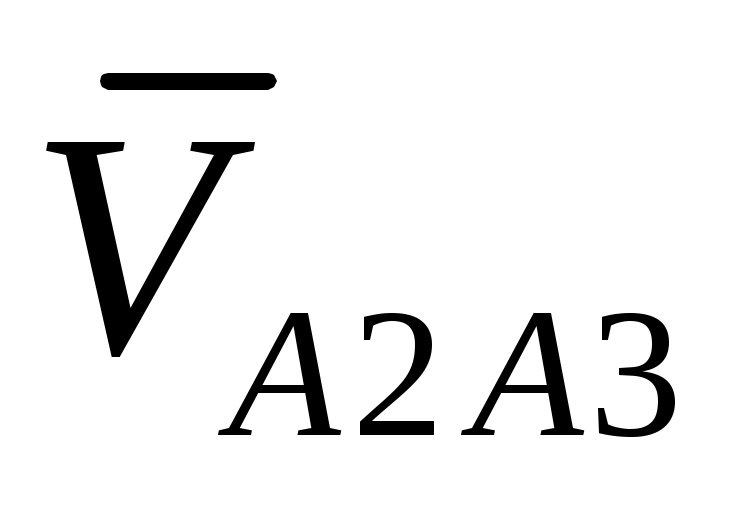 - скорость т.
- скорость т. при относительном движении звена 2 по звену 3.
при относительном движении звена 2 по звену 3.
Из (4.6) можно получить уравнение с неизвестным вектором в левой части:
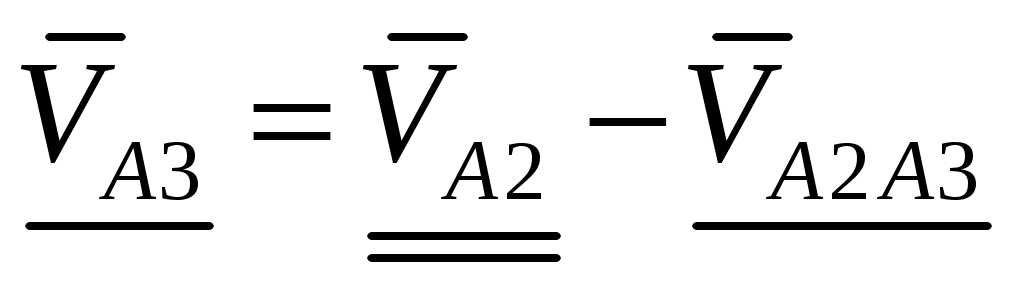 (4.7)
(4.7)
Для графического решения уравнения (4.7) из полюса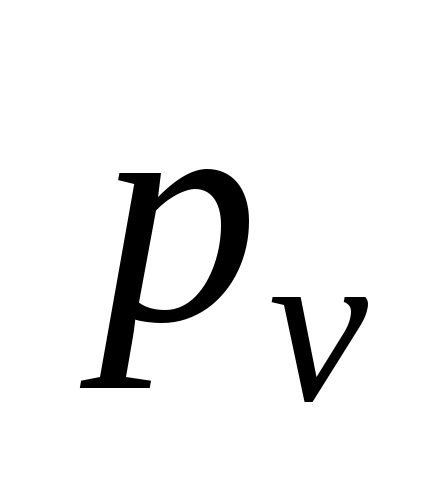 в масштабе
в масштабе 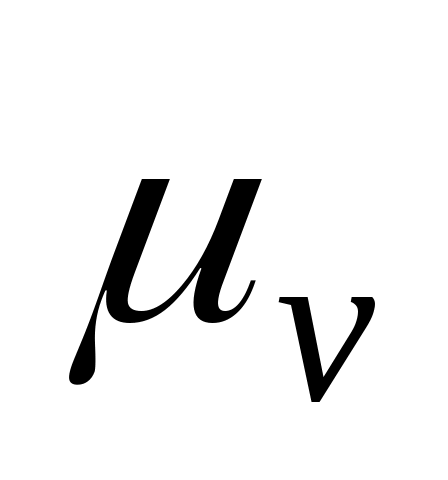 откладываем известный вектор
откладываем известный вектор 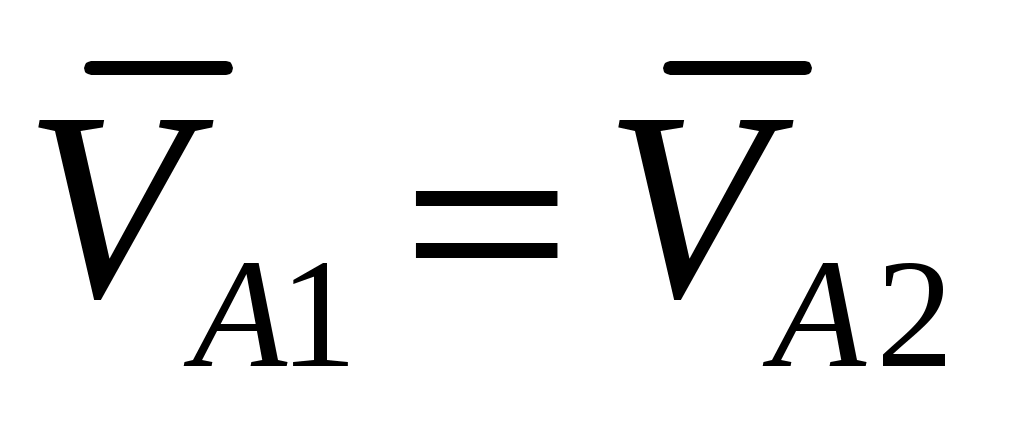 (Рис.4.8). Через точку
(Рис.4.8). Через точку 
(или совпадающую с ней точку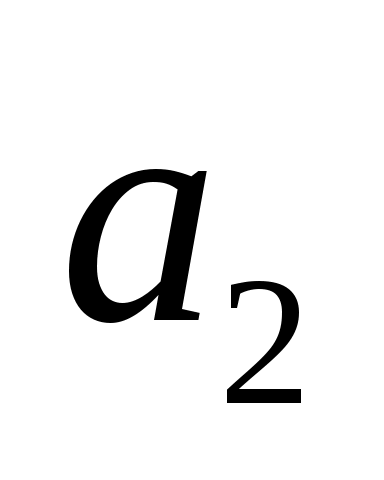 ) конца векторов
) конца векторов  проводим прямую, направленную параллельно
проводим прямую, направленную параллельно 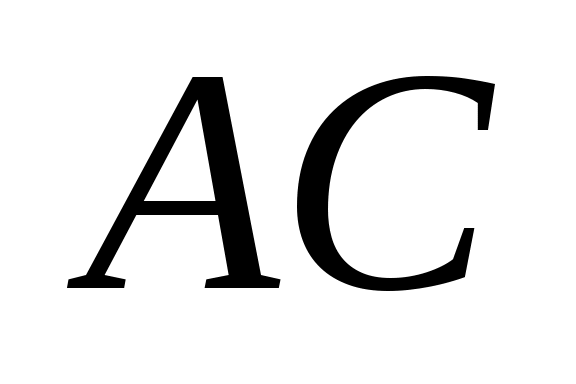 . На этой прямой будет находиться вектор
. На этой прямой будет находиться вектор  . Одновременно, через полюс
. Одновременно, через полюс 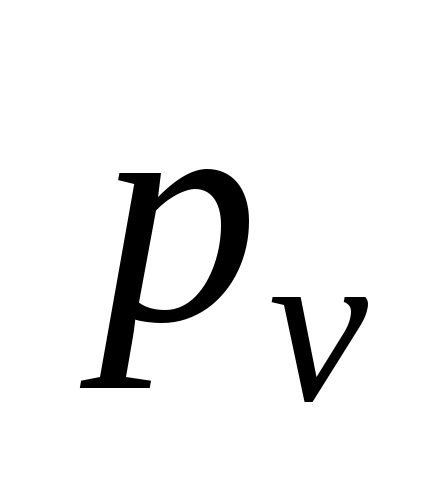 проводим прямую, перпендикулярную
проводим прямую, перпендикулярную 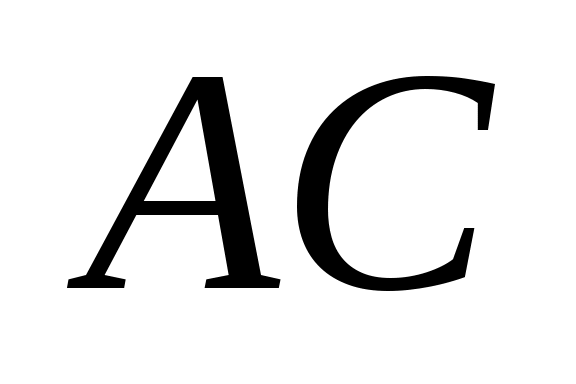 . На ней будет лежать вектор
. На ней будет лежать вектор  . Пересечение этих прямых даст точку
. Пересечение этих прямых даст точку 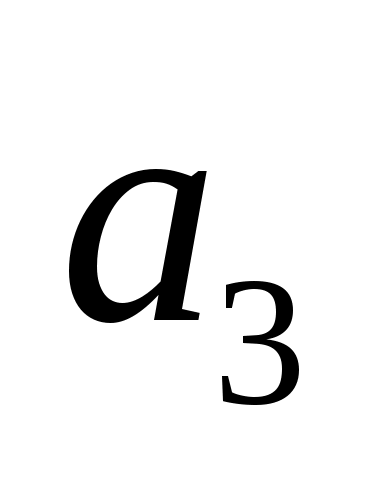 , определяющую величины векторов
, определяющую величины векторов 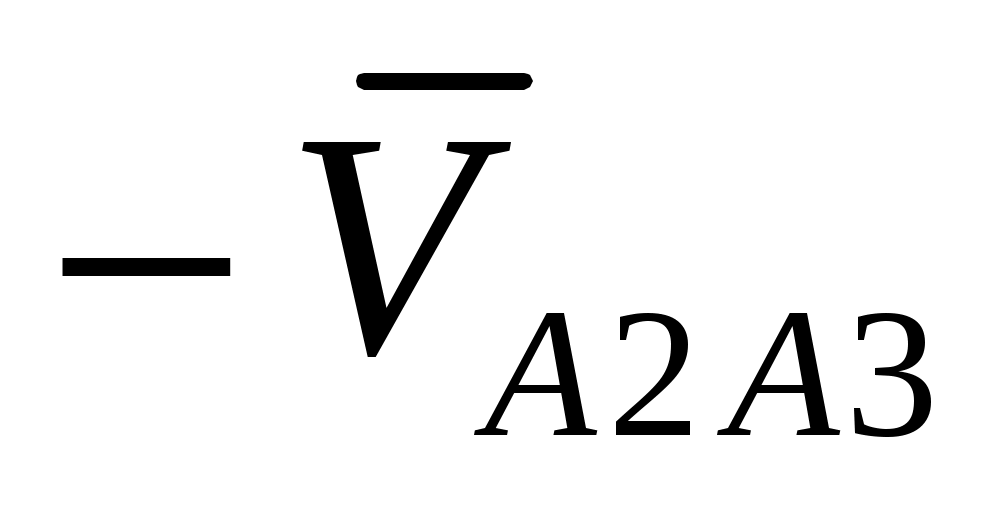 и
и  .
.
Если скорость т.
т. известна, то легко определить скорость т.
известна, то легко определить скорость т.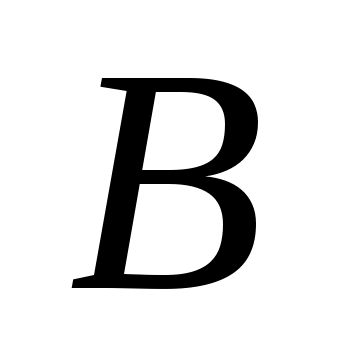 , также принадлежащей звену 3, которое вращается вокруг т.
, также принадлежащей звену 3, которое вращается вокруг т. (см. п.4 алгоритма).
(см. п.4 алгоритма).
Построение плана скоростей для данной задачи можно представить в виде алгоритма действий, приведенного ниже.
Как и планы скоростей, планы ускорений, как правило, строят не ради самих ускорений, а с целью дальнейшего их использования.
Одно из возможных направлений этого использования - силовой анализ механизма. Если силовой расчет выполняется по методу кинетостатики, ускорения необходимы для определения фиктивных сил инерции (сил инерции Даламбера). Таким образом, определение ускорений (как и определение скоростей) - не самоцель. Обычно, это промежуточный этап решения более сложной задачи.
Рассмотрим построение планов ускорений на примерах 2-х простых механизмов.
Постановка задачи
Дано:
Определить:
Пример 1. – кривошипно-коромысловый механизм (Рис.4.9)
Решение
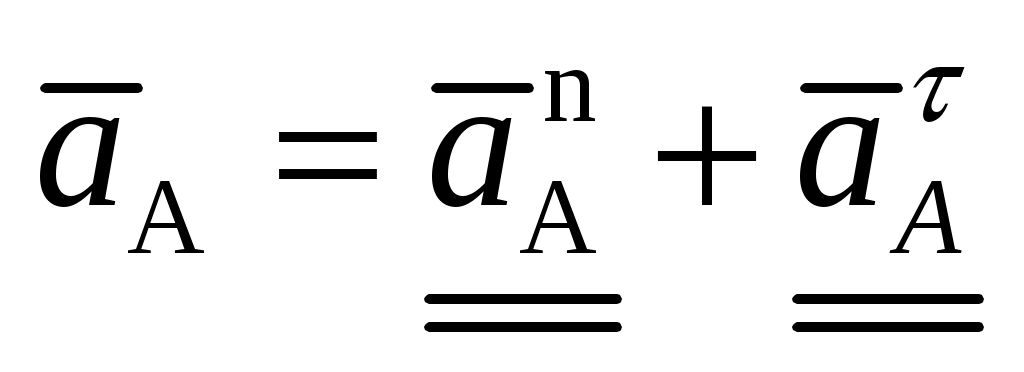 (4.8)
(4.8)
 (4.9)
(4.9)
Направления: (Рис.4.10)
(Рис.4.10)
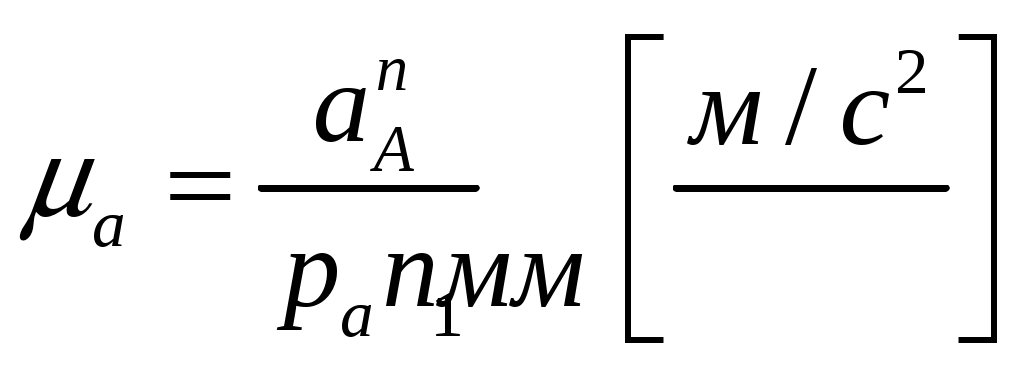 (4.10)
(4.10)
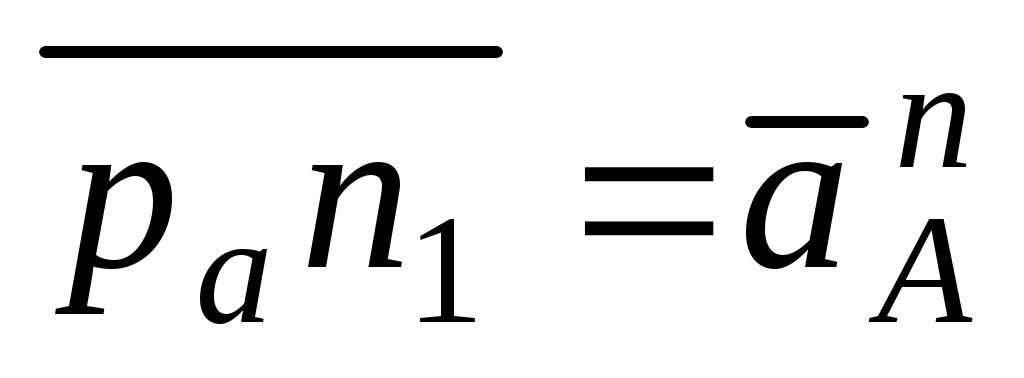 ;
; 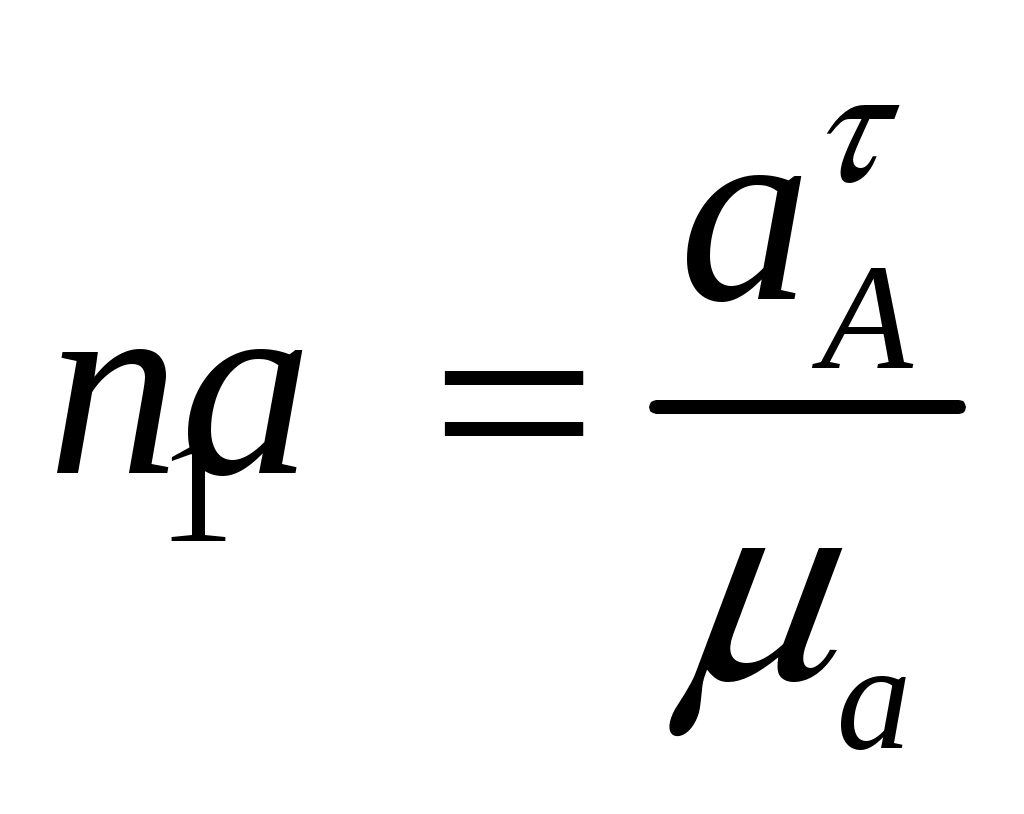 ;
; 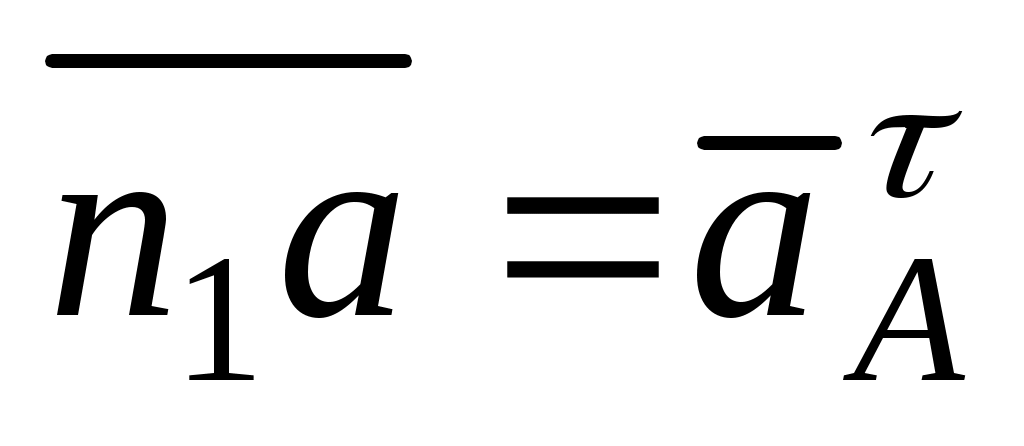 ;
; 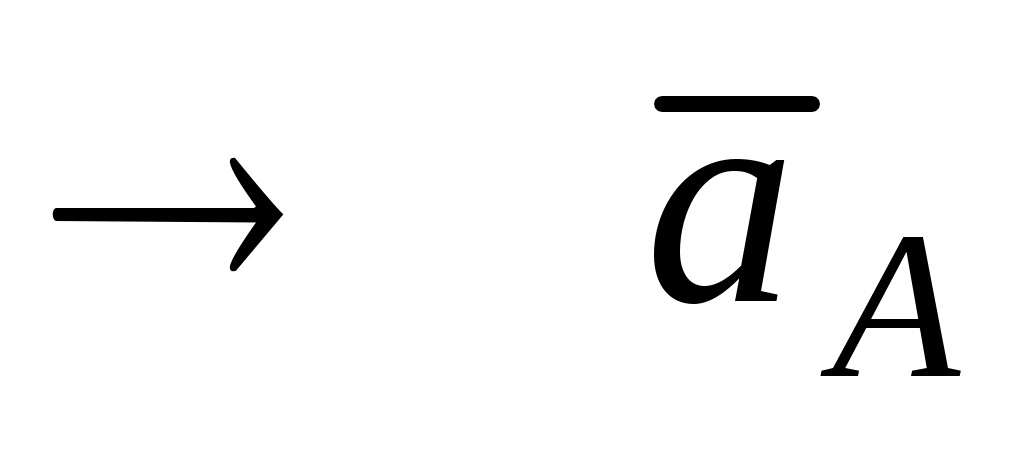
Базовый план скоростей построен.
Переходим к определению скоростей других точек. Такой точкой по условию задачи является точка
-
Определим скорость точки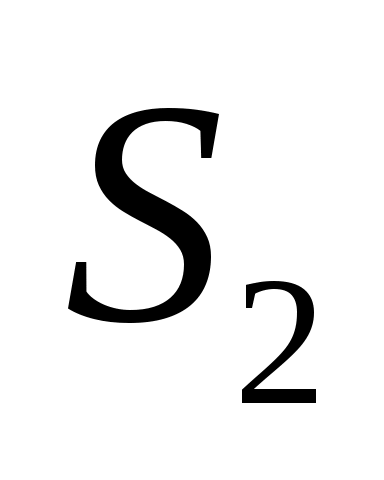 .
.
Скорость т.
-
Определим угловые скорости звеньев 2 и 3:
Угловые скорости
Направления
Пример 2.
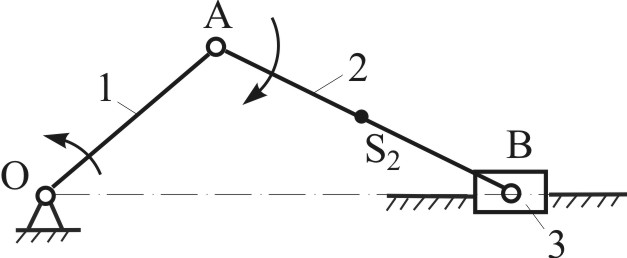 | 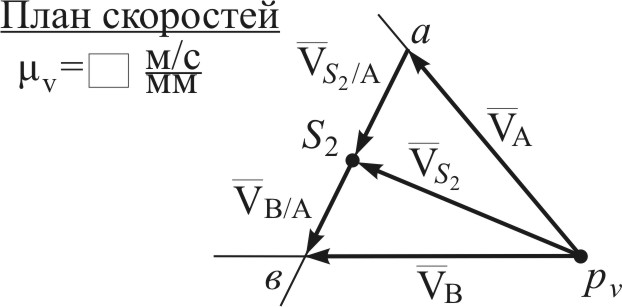 |
| Рис.4.5 | Рис. 4.6 |
Дано:
кривошипно-ползунный механизм (Рис.4.5) в заданном положении;
звено 1 – входное; 1 - угловая скорость звена 1; AS2 = 0,5 · AB.
Определить:
скорости точек А, В, S2 путем построения плана скоростей.
Решение
Последовательность и логика построений в данной задаче и в Примере 1 являются аналогичными. Поэтому, решение приводим в конспективном виде.
-
 ;
; -
 ;
; -
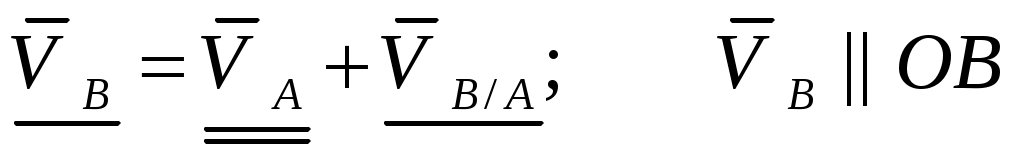 ;
; 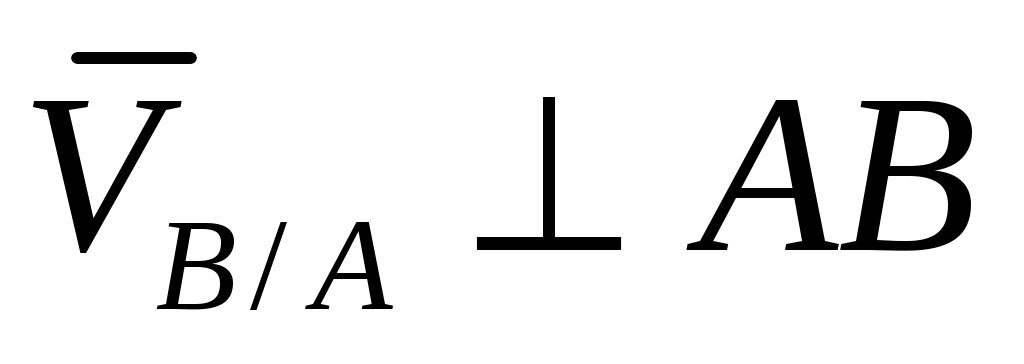

 ;
; 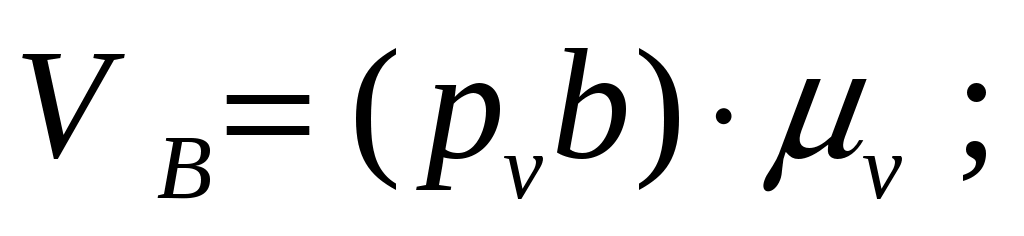
-
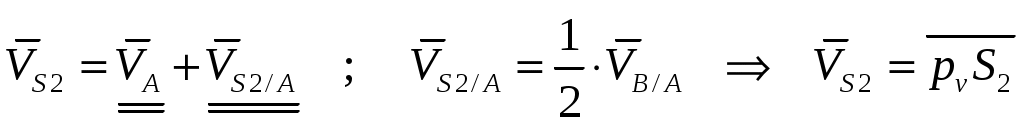 ;
; 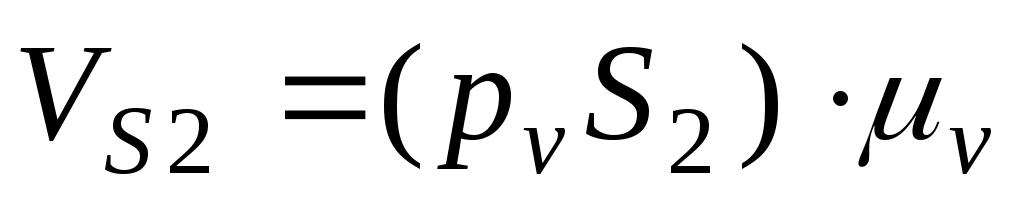 ;
; -
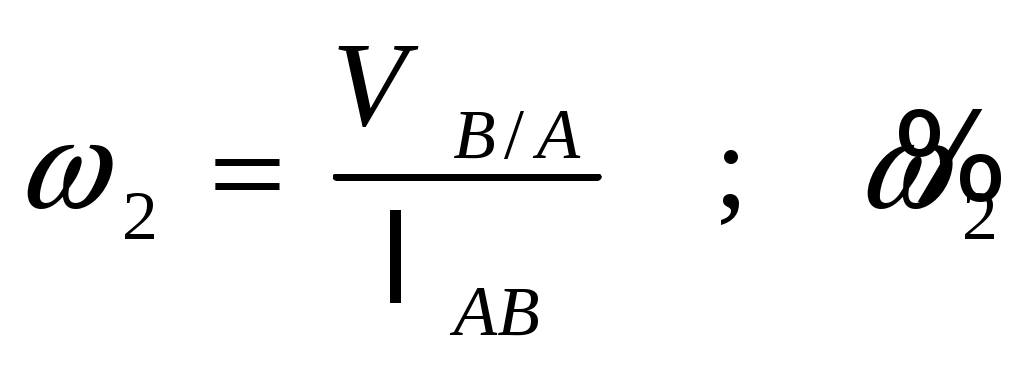
Пример 3.
 |  |
| Рис. 4.7 | Рис. 4.8 |
Дано:
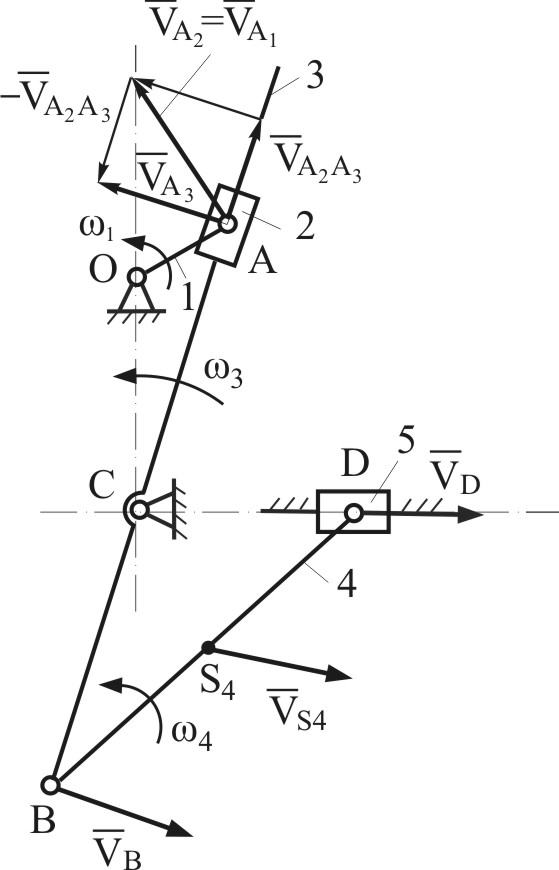
кривошипно-ползунный механизм с промежуточной кулисой (Рис.4.7) в заданном положении; звено 1 – входное; 1 - угловая скорость звена 1;
ВS4 = 0,5 · BD.
Определить:
скорости точек A, B, D, S4 путем построения плана скоростей.
Решение.
Ряд пунктов приведенного ниже алгоритма выполняются аналогично предыдущим примерам и не требуют пояснений. Затруднения могут возникнуть при определении скоростей точек структурной группы (2,3), звенья которой образуют между собой поступательную пару. Построение плана скоростей в этом случае имеет свои особенности, на которые следует обратить внимание (см. пп.2-3 алгоритма).
При построении планов скоростей кулисных механизмов характерным является использование уравнений, связывающих скорости двух точек, совпадающих в данном положении, но принадлежащих разным звеньям поступательной пары. В нашем примере таким точками будут точки
(Рис.4.7). Точки
Рассматривая движение звена 2 как сложное, представим его в виде суммы двух движений: переносного вращательного со звеном 3 и относительного поступательного вдоль звена 3.
Тогда, для точки
где
Из (4.6) можно получить уравнение с неизвестным вектором в левой части:
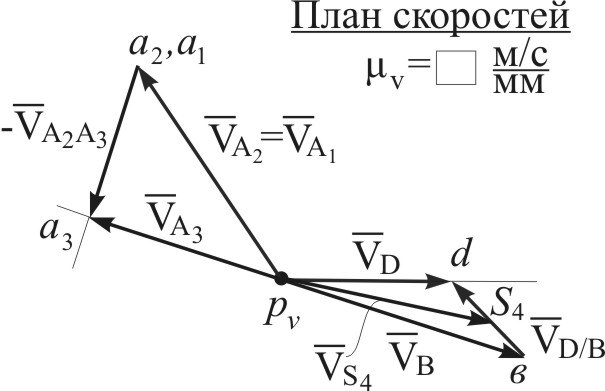
Для графического решения уравнения (4.7) из полюса
(или совпадающую с ней точку
Если скорость
Построение плана скоростей для данной задачи можно представить в виде алгоритма действий, приведенного ниже.
-
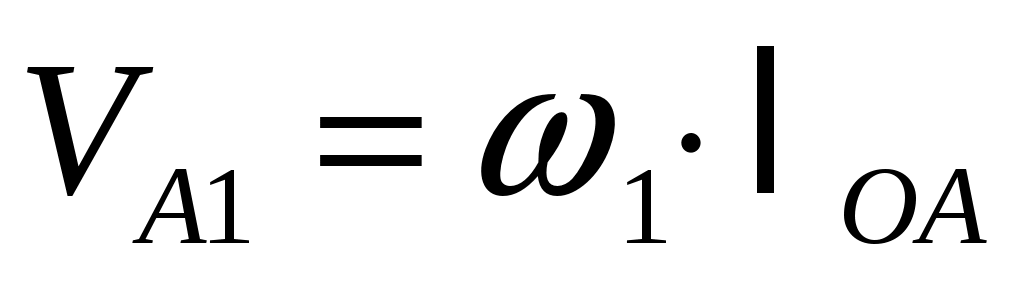 ;
;  ;
; 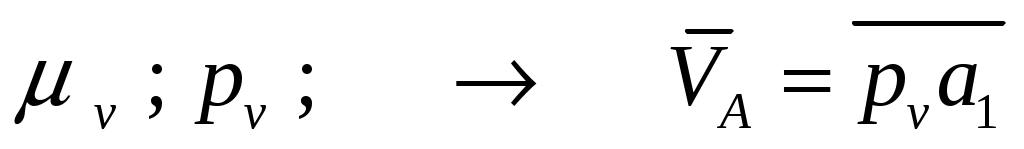 (Рис.4.8);
(Рис.4.8); -
 ;
;  ;
; -
 ;
; 

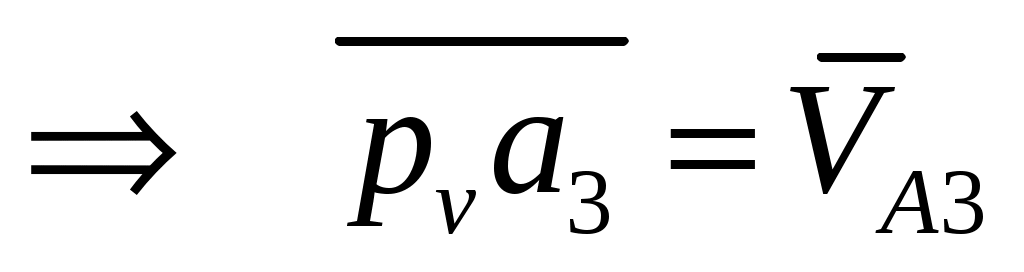 ;
;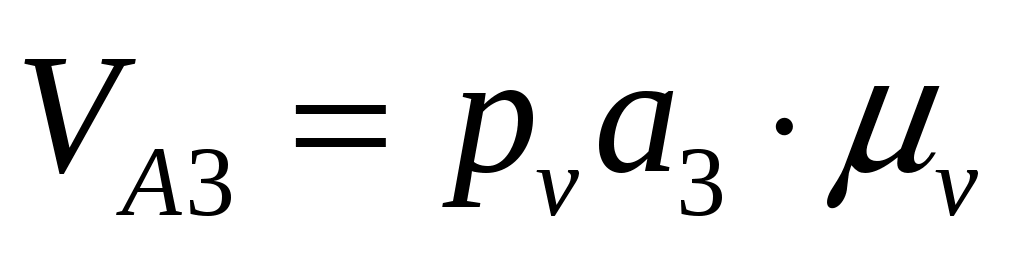 ;
; -
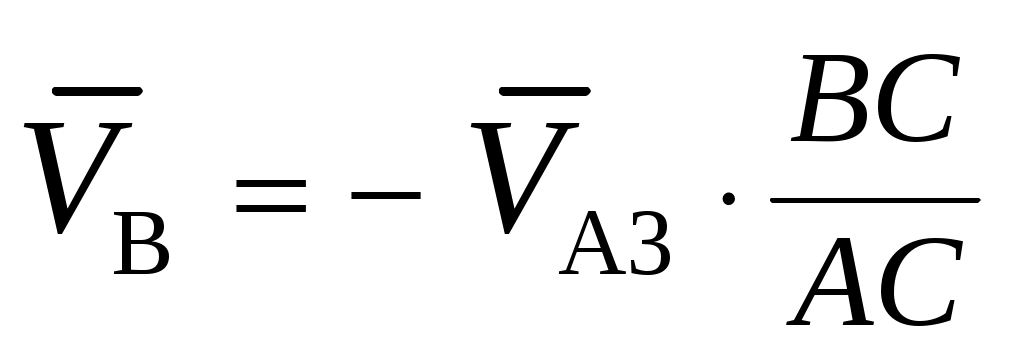 ;
; -
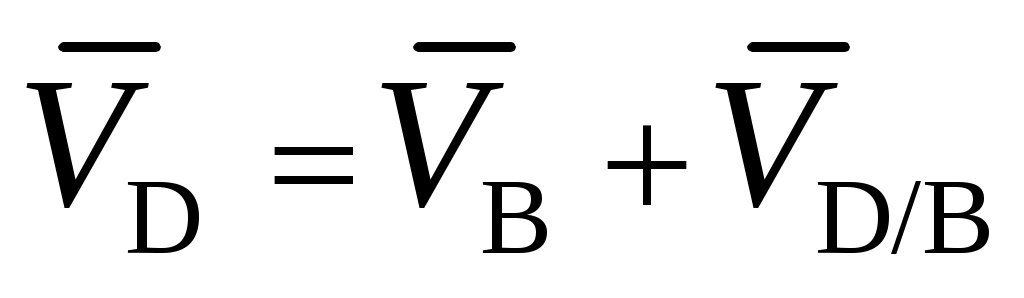 ;
; 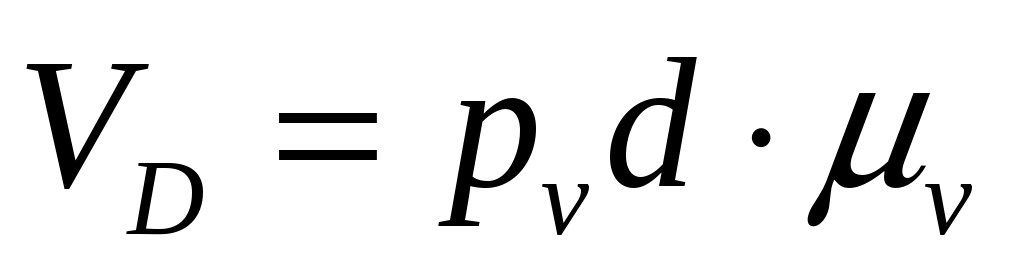 ;
; -
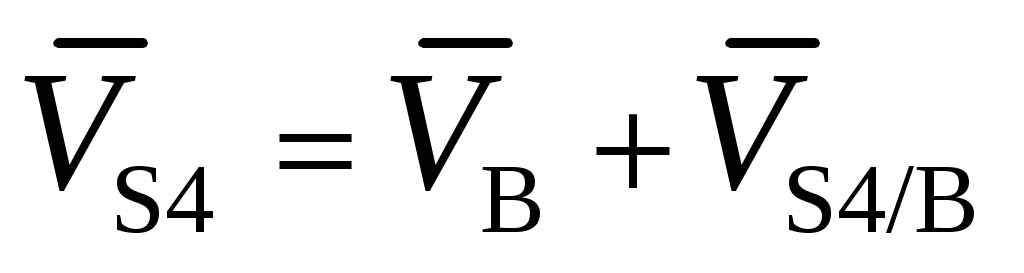 ,
, 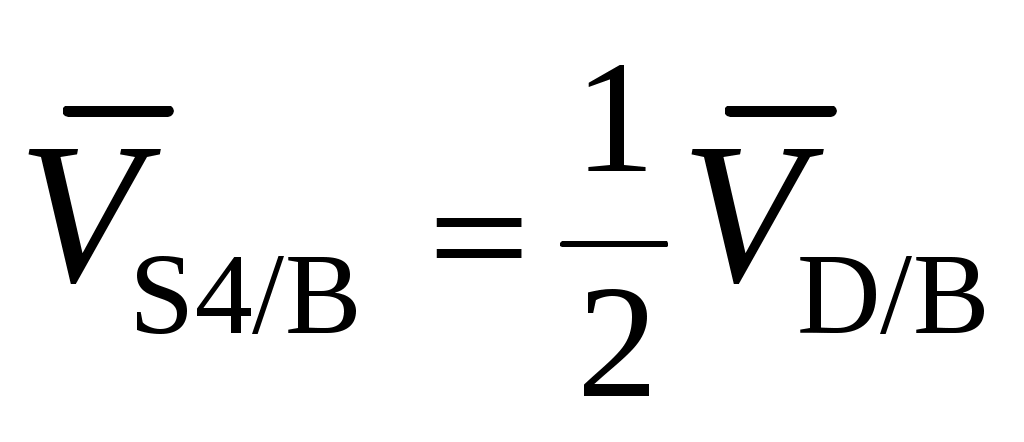 ;
; -
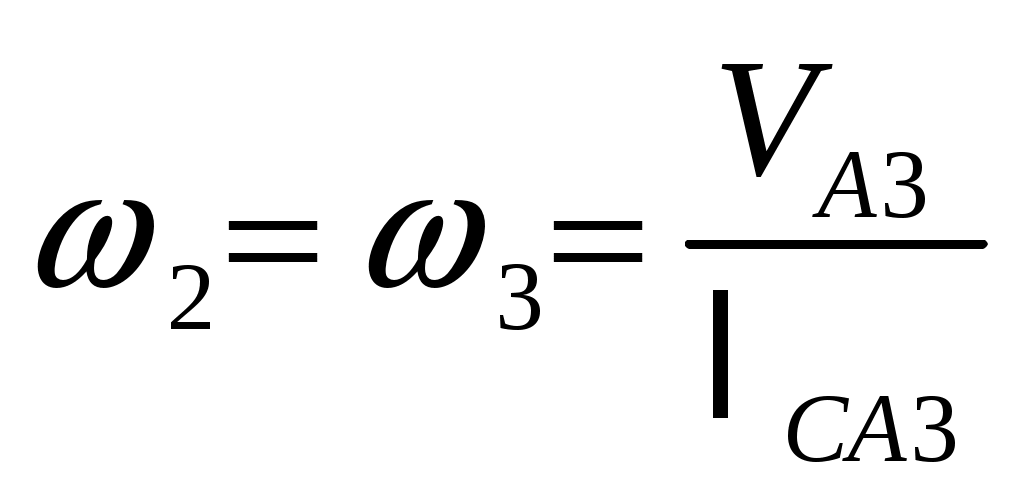 ;
; 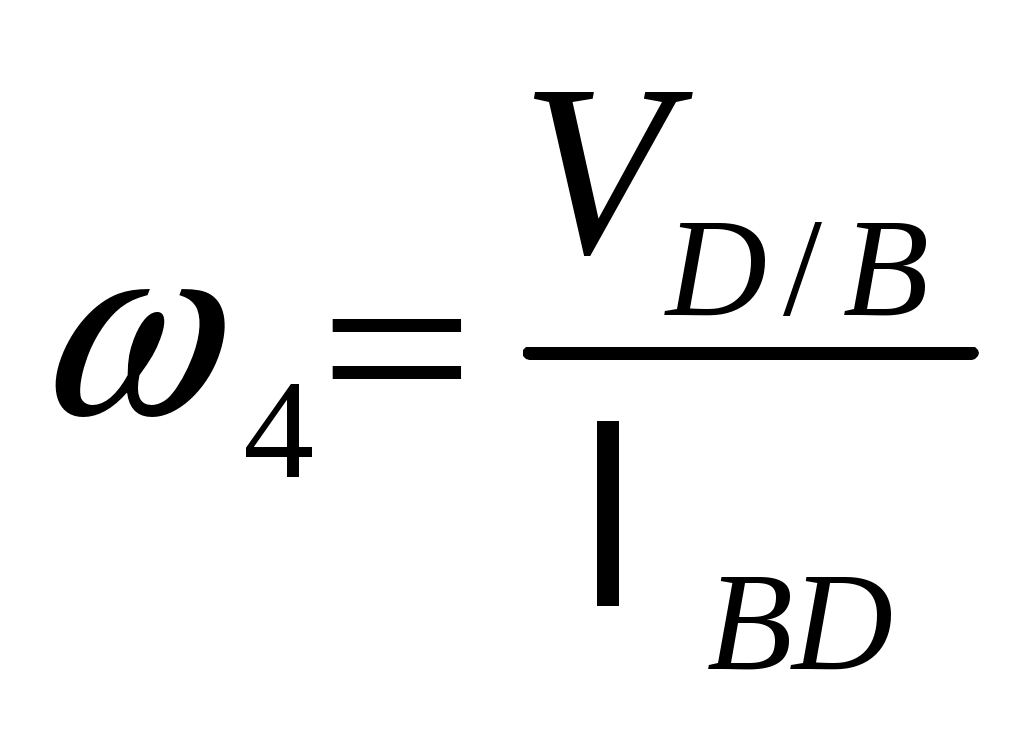 ;
; 
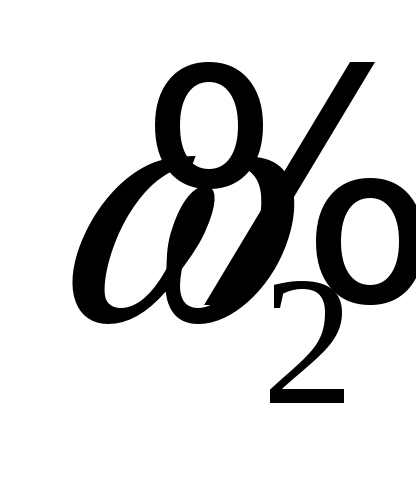 ;
; 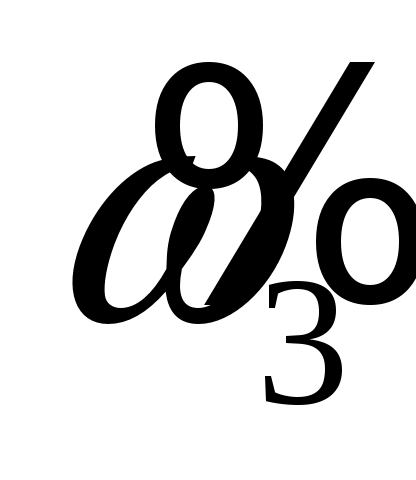 ;
; 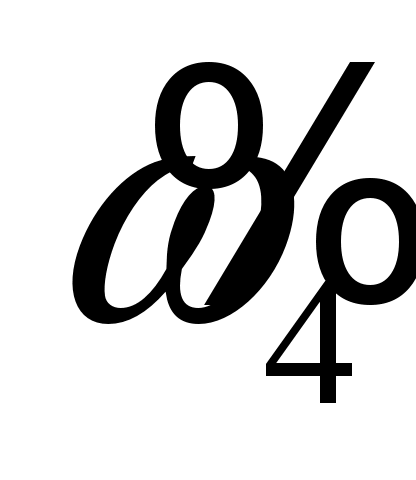 .
.
-
Определение ускорений точек (построение планов ускорений) и угловых ускорений звеньев механизма
Как и планы скоростей, планы ускорений, как правило, строят не ради самих ускорений, а с целью дальнейшего их использования.
Одно из возможных направлений этого использования - силовой анализ механизма. Если силовой расчет выполняется по методу кинетостатики, ускорения необходимы для определения фиктивных сил инерции (сил инерции Даламбера). Таким образом, определение ускорений (как и определение скоростей) - не самоцель. Обычно, это промежуточный этап решения более сложной задачи.
Рассмотрим построение планов ускорений на примерах 2-х простых механизмов.
Постановка задачи
Дано:
-
План механизма в заданном положении. -
Угловая скорость и угловое ускорение ведущего звена. -
Угловые скорости всех других звеньев механизма.
Определить:
-
Ускорения характерных точек (точки соединения звеньев). -
Ускорения других точек. -
Угловые ускорения звеньев.
Пример 1. – кривошипно-коромысловый механизм (Рис.4.9)
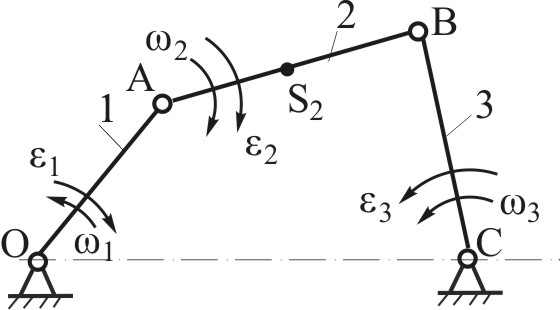 | 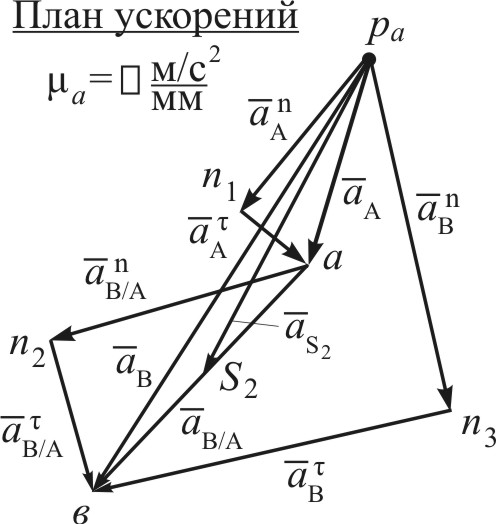 |
| Рис. 4.9 | Рис. 4.10 |
Решение
-
Определим ускорение точки А
Направления:
-
Выберем масштабный коэффициент плана ускорений и построим вектор :
:
-
Определим ускорение точки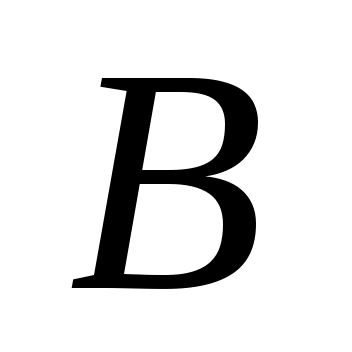 (точка
(точка 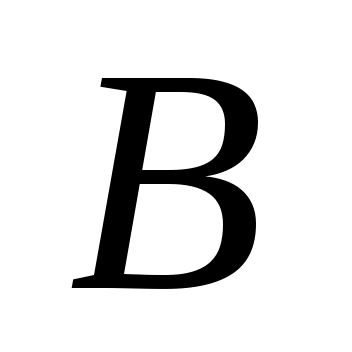 принадлежит 2-м звеньям)
принадлежит 2-м звеньям)

