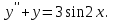Файл: Методические указания по выполнению практических заданий по дисциплине математика ( О. 7) для специальности 23. 05. 05 Системы обеспечения движения поездов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 40
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Пример. Найти общее решение уравнения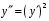
.
Замена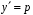
, 
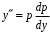д.у. : 
.
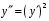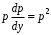Особое решение: р = 0;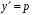
; у = С.
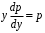– уравнение с разделяющимися переменными.
Общее решение д.у.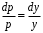
: 
.
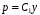Общий интеграл д.у.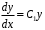
: 
.
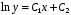Пример. Найти общее решение уравнения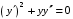
.
; 
; 
.
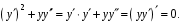
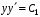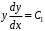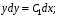
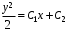Пример. Найти общее решение уравнения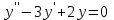
.
Корни характеристического уравнения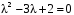
: 
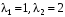. Общее решение: 
.
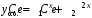Пример. Найти общее решение уравнения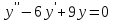
.
Корни характеристического уравнения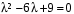
: 
.
Общее решение: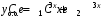
.
Пример. Найти общее решение уравнения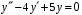
.
Корни характеристического уравнения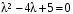
:
.
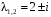Общее решение:
.
Пример. Записать линейное однородное дифференциальное уравнение, общим решением которого является функция
.
Корни характеристического уравнения: l1 = 0, l2 = –4.
Характеристическое уравнение: (l – l1) (l – l2) = 0 или l2 + 4l = 0.
Линейное однородное дифференциальное уравнение: у² + 4у¢ = 0.
Пример. Для дифференциального уравнения yIV + y¢¢¢ + 4y¢ + y = 0 составить характеристическое уравнение.
Характеристическое уравнение: l4 +l3+4l + 1 = 0.
Пример. Найти общее решение уравнения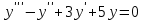
.
Характеристическое уравнение: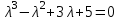
.
Корни характеристического уравнения: l1 = –1,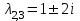
.
Общее решение д.у.: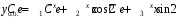
.
Пример. Найти общее решение уравнения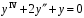
.
Характеристическое уравнение: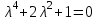
.
Корни характеристического уравнения: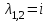
, 
.
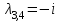Общее решение уравнения: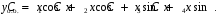
Пример. Доказать, что при комплексных корнях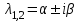
характеристического уравнения функци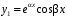и 
и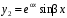 
образуют фундаментальную систему.
Два частных решения д.у. при комплексных корнях:
,
.
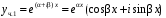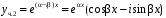Линейные комбинации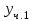
, 
:
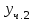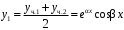и 
.
– 
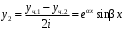
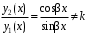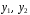образуют фундаментальную систему решений.
Пример. Доказать, что при кратных корнях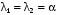
характеристического уравнения 
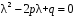функци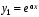и 
и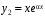 
образуют фундаментальную систему.
При одинаковых корнях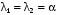 характеристического уравнения 
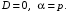Одно частное решение имеет вид 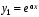. Второе частное решение ищется в виде 
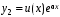. Подставив в уравнение у² – 2ру¢ + qу = 0 функции 
, 
, 
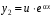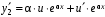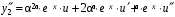, получим
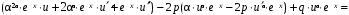
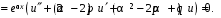
Второе и третье слагаемые в скобках обращаются в ноль, т.к. a – корень уравнения и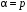
. Любое частное решение уравнения 
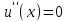задает функцию 
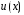, например, 
. 
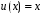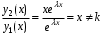– функци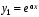и и 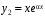образуют фундаментальную систему.
Пример. Методом вариации произвольных постоянных найти общее решение уравнения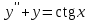
.
Соответствующее однородное уравнение:
.
Характеристическое уравнение:
.
Корни характеристического уравнения:
, 
.;
Фундаментальная система решений: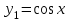
, 
.
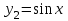Общее решение однородного д.у.: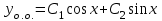
.
Частное решение неоднородного д.у.: уч.н.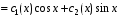
.
Система уравнений для нахождения функций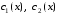
:
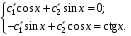
Решения системы: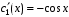
, 
.
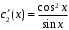Искомые функции: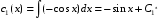
,
.
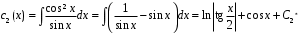Частное решение при
:
.
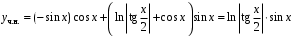Общее решение неоднородного д.у.:
.
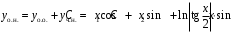Пример. Доказать, что если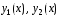
– фундаментальная система решений однородного д.у. 
, то для неоднородного д.у. 
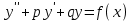решение системы 
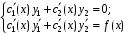задает частное решение 
.
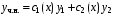Производная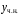
: 
.
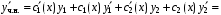
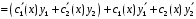Пусть функции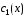
, 
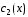таковы, что 
.
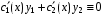Тогда
.
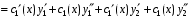
Подстановка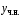
, 
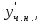
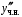в уравнение 
приводит к равенству
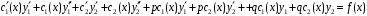или
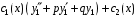
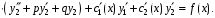
Выражения в скобках левой части равенства обращаются в ноль и уравнение принимает вид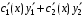
.
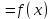Пример. Записать вид частного решения неоднородного д.у., если правая часть этого уравнения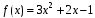
и среди корней характеристического уравнения нет нулевого корня.
Число m = 0 не совпадает с корнями характеристического уравнения:r = 0.
Вид частного решения: yч.н. = Mх2 + Nх + K (строка 6 таблицы 13.3).
Пример. Установить вид частного решения уравнения у² – 5у¢ = 7х + 8.
Соответствующее однородное уравнение: у² – 5у¢ = 0.
Характеристическое уравнение: l2 – 5l = 0.
Корни характеристического уравнения l1 = 5, l2 = 0;
Одно совпадение числа m = 0 с корнем характеристического уравнения: r = 1.
Правая часть дифференциального уравнения: f(x) = 7x +8.
Вид частного решения:
yч.н. = х(Mx + N) = Mx2 + Nх (строка 5 таблицы 13.3).
Пример. Записать вид частного решения неоднородного д.у., если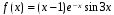
и среди корней характеристического уравнения есть пара комплексных сопряжённых корней 
Число повторений r числа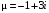
среди корней характеристического уравнения: 1.
Вид частного решения: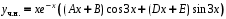
.
Пример.Найти общее решение дифференциального уравнения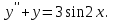
Пример. Найти общее решение уравнения
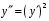.Замена
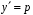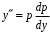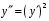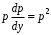, д.у. : .Особое решение: р = 0;
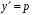; у = С. 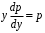– уравнение с разделяющимися переменными.Общее решение д.у.
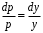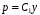: .Общий интеграл д.у.
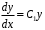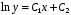: .Пример. Найти общее решение уравнения
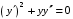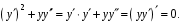
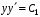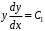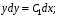
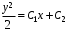. ; ; .Тема 4
Линейные однородные уравнения с постоянными коэффициентами
Пример. Найти общее решение уравнения
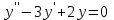.Корни характеристического уравнения
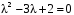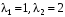: . Общее решение: 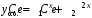.Пример. Найти общее решение уравнения
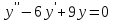.Корни характеристического уравнения
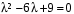: . Общее решение:
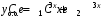.Пример. Найти общее решение уравнения
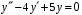.Корни характеристического уравнения
:
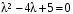
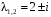. Общее решение:
.Пример. Записать линейное однородное дифференциальное уравнение, общим решением которого является функция
. Корни характеристического уравнения: l1 = 0, l2 = –4.
Характеристическое уравнение: (l – l1) (l – l2) = 0 или l2 + 4l = 0.
Линейное однородное дифференциальное уравнение: у² + 4у¢ = 0.
Пример. Для дифференциального уравнения yIV + y¢¢¢ + 4y¢ + y = 0 составить характеристическое уравнение.
Характеристическое уравнение: l4 +l3+4l + 1 = 0.
Пример. Найти общее решение уравнения
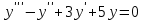.Характеристическое уравнение:
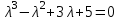.Корни характеристического уравнения: l1 = –1,
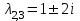. Общее решение д.у.:
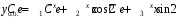.Пример. Найти общее решение уравнения
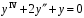.Характеристическое уравнение:
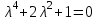.Корни характеристического уравнения:
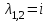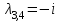, .Общее решение уравнения:
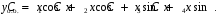
Пример. Доказать, что при комплексных корнях
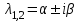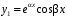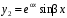характеристического уравнения функции и образуют фундаментальную систему. Два частных решения д.у. при комплексных корнях:
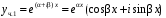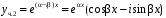, .Линейные комбинации
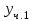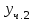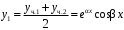, : и
.
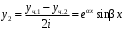
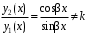– образуют фундаментальную систему решений.Пример. Доказать, что при кратных корнях
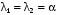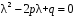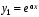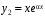характеристического уравнения функции и образуют фундаментальную систему.При одинаковых корнях
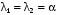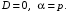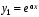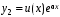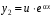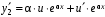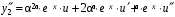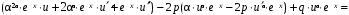
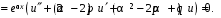
характеристического уравнения Одно частное решение имеет вид . Второе частное решение ищется в виде . Подставив в уравнение у² – 2ру¢ + qу = 0 функции , , , получим Второе и третье слагаемые в скобках обращаются в ноль, т.к. a – корень уравнения и
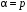. Любое частное решение уравнения 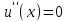задает функцию 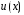, например, 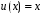. 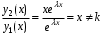– функци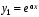и и 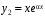образуют фундаментальную систему. Тема 5
Линейные неоднородные уравнения с постоянными коэффициентами. Метод Лагранжа
Пример. Методом вариации произвольных постоянных найти общее решение уравнения
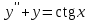.Соответствующее однородное уравнение:
. Характеристическое уравнение:
.
Корни характеристического уравнения:
, .; Фундаментальная система решений:
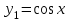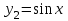, . Общее решение однородного д.у.:
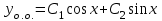.Частное решение неоднородного д.у.: уч.н.
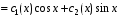.Система уравнений для нахождения функций
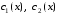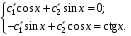
: Решения системы:
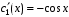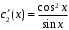, .Искомые функции:
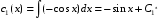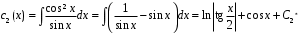, .Частное решение при
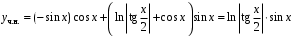: .Общее решение неоднородного д.у.:
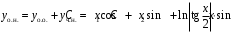.Пример. Доказать, что если
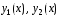– фундаментальная система решений однородного д.у. 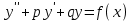, то для неоднородного д.у. решение системы 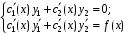задает частное решение 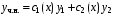. Производная
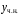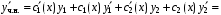
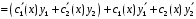: .Пусть функции
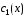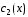, таковы, что 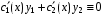. Тогда
.
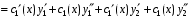
Подстановка
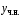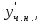
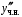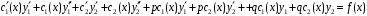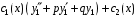
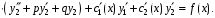
, в уравнение приводит к равенству или Выражения в скобках левой части равенства обращаются в ноль и уравнение принимает вид
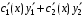
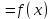.Темы 6,7
Линейные неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов
Пример. Записать вид частного решения неоднородного д.у., если правая часть этого уравнения
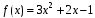и среди корней характеристического уравнения нет нулевого корня.Число m = 0 не совпадает с корнями характеристического уравнения:r = 0.
Вид частного решения: yч.н. = Mх2 + Nх + K (строка 6 таблицы 13.3).
Пример. Установить вид частного решения уравнения у² – 5у¢ = 7х + 8.
Соответствующее однородное уравнение: у² – 5у¢ = 0.
Характеристическое уравнение: l2 – 5l = 0.
Корни характеристического уравнения l1 = 5, l2 = 0;
Одно совпадение числа m = 0 с корнем характеристического уравнения: r = 1.
Правая часть дифференциального уравнения: f(x) = 7x +8.
Вид частного решения:
yч.н. = х(Mx + N) = Mx2 + Nх (строка 5 таблицы 13.3).
Пример. Записать вид частного решения неоднородного д.у., если
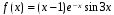и среди корней характеристического уравнения есть пара комплексных сопряжённых корней Число повторений r числа
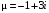среди корней характеристического уравнения: 1.Вид частного решения:
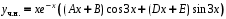.Пример.Найти общее решение дифференциального уравнения