Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 354
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
Дифференциальные уравнения
С помощью пакета MathCad можно решать как обыкновенные дифференциальные уравнения, так и уравнения в частных производных. Также есть возможность решать системы дифференциальных уравнений.
Решение осуществляется посредством разных численных методов, для которых MathCad имеет различные встроенные функции. Результат выдается в виде значений искомой функции на некоторой сетке.
Рассмотрим простейшие примеры.
Пример. Решить ОДУ первого порядка у +3у = 0 при у(0)= 4.
Решение. Для решения уравнения используем метод Рунге-Кутта четвертого порядка. Он встроен в пакет и называется функцией RKFIXED.
-
зададим вектор начальных условий. Так как у нас уравнение первого порядка, то имеется единственный элемент данного вектора:
у0 := 4
-
теперь зададим функцию D, равную значению первой производной искомой функции в начальном пункте. Так как у = -3y, то
D(x,y) := -3у0
-
зададим интервал [х1,х2], на котором ищется решение нашего уравнения:
х1 := 0 х2 := 4
-
определим количество точек, в которых ищется решение:
n := 100
-
вызываем функцию поиска решения методом Рунге-Кутта:
z := rkfixed(y, х1, х2, n, D)
Получим матрицу z, состоящую из двух столбцов. Первый столбец содержит точки, в которых ищется решение дифференциального уравнения. Второй содержит значения найденного решения в соответствующих точках. Теперь мы можем вывести это решение как матрицу, введя:
z =
л
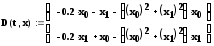
ибо вывести его в виде графика, использовав соответствующие столбцы для его построения.
Аналогично решаются ОДУ более высоких порядков, отличия только в количестве столбцов векторов у, D и результирующей матрицы.
Таким же образом с помощью функции rkfixed решаются и системы дифференциальных уравнений.
Пример. Решить систему двух нелинейных дифференциальных уравнений первого порядка:
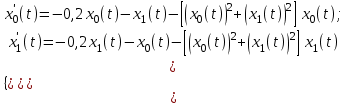
Р

ешение.
—
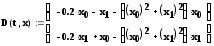
первые производные искомых функций (здесь переменные х0 и х1 – переменные с индексом);
t1 := 0 t2 := 20 — интервал поиска решения;
n := 100 — количество точек в заданном интервале;
z := rkfixed(x, t1, t2, n, D) — матрица решения.
Находим матрицу решений z, у которой первый столбец – точки, в которых ищется приближенное решение, а остальные столбцы содержат значения найденных решений в этих точках.
Задание
Решить дифференциальное уравнение:
а)
 ; б)
; б) 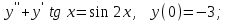
в)
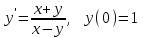 ; г)
; г) 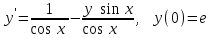 .
.Контрольные вопросы
-
Перечислите символьные операции преобразования. -
Какие параметры определяет стиль представления результатов вычислений и где он задается? -
В каких случаях результат символьных преобразований помещается в буфер обмена? -
Для чего необходимо задание операторов пользователя? -
Как задать оператор пользователя?
Список используемых источников
Основная литература
-
Гаврилов М.В. Информационные технологии учебник для бакалавров- М.: Изд. Юрайт, 2014г.-350с. -
Киреева Г.И. Основы информационных технологий: учебное пособие. Изд-во: ДМКПресс, 2014г. ЭБС «Издательства Лань» http://e.lanbook.com/view/book/ -
Михеева Е.В. Информатика: учебник для студ. учреждений сред. проф. образования/ Е. В. Михеева, О.И. Титова. -3-е изд., стер. - М.: Издательский центр «Академия», 2014, - 352с. -
Кирьянов Д.В. MathCAD13. – Спб.: БХВ – Петербург, 2014. -
Макаров Е.Г. Инженерные расчеты в MathCAD: Учебный курс. – Спб.: Питер, 2014. -
Гурский Д. А., Турбина Е. С. Вычисления в MathCAD12. – Спб.: Питер, 2014.- 544 с.: ил.
Дополнительная литература:
-
Гвоздева В.А. Основы построения автоматизированных информационных систем: учебник- М.: ИД «Форум»: ИНФРА-М, 2015г.-320с. -
Партыка Т.Л. Информационная безопасность: учебное пособие для СПО-М.:ФОРУМ, 2015г.-432с. -
Алексеев Г.В., Бриденко И.И., Головацкий В.А., Верболоз Е.И. Компьютерные технологии при проектировании и эксплуатации технологического оборудования. Изд-во: СПб. ГЕОРД ,2015г.- 252 с. ЭБС «Издательства Лань» http://e.lanbook.com/view/book/4878/ -
Жданов С.А. Информационные системы: учебник для студентов ВО. Изд-во: «Прометей», 2015г. ЭБС «Издательства Лань» http://e.lanbook.com/view/book/ -
Шаньгин В.Ф. Защита информации в компьютерных системах и сетях. Изд-во: ДМКПресс, 2015г. ЭБС «Издательства Лань» http://e.lanbook.com/view/book/ -
Бирюков А.А. Информационная безопасность: защита и нападение. Изд-во: ДМКПресс, 2015г. ЭБС «Издательства Лань» http://e.lanbook.com/view/book/ -
Ерохин В.В. Безопасность информационных систем. Изд-во: Флинта ЭБС «Издательства Лань» http://e.lanbook.com/view/book/ -
Ляхович В.Ф.Основы информатики: учебник. Изд-во: КноРус, 2016г. — 347 с. ЭБС «BOOK.ru» https://www.book.ru/ book /919275/view
-
Могилев А.В. Практикум по информатике: учебное пособие для студ. высш. учебн. заведений/ А.В. Могилев, Н. И. Пак, Е.К. Хеннер; под ред Е.К. Хеннера. -5-е изд., стер.- М.: Издательский центр «Академия», 2014.-608с. -
Информатика и ИКТ. Учебник. 11 класс. Базовый уровень / Под ред. проф. Н.В. Макаровой. – Спб.: Питер, 2014.-224с.: ил. -
Шафрин Ю.А. Информатика. Информационные технологии. Том 1-2. – М., 2014. -
Журнал «Мир ПК» 2016г.-№№ 1-12 -
Журнал «CHIP C DVD/ ЧИП С DV» 2012г.-№№ 1-12,2013г. -№№ 1-12, 2014г. -№№ 1-12, 2015г.-№№ 1-12 -
Журнал «КомпьютерПресс» 2012г.-№№ 1-12,2013г. -№№ 1-12, 2014г .-№№ 1-6 -
Журнал «Компоненты и технологии» 2016г.-№№1-12, 2017г.-№№1-6
Интернет – ресурсы:
-
http://iit.metodist.ru - Информатика - и информационные технологии: сайт лаборатории информатики МИОО -
http://www.intuit.ru - Интернет-университет информационных технологий (ИНТУИТ.ру) -
http://test.specialist.ru - Онлайн-тестирование и сертификация по информационным технологиям -
http://www.iteach.ru - Программа Intel «Обучение для будущего» -
http://www.rusedu.info - Сайт RusEdu: информационные технологии в образовании -
http://www.osp.ru - Открытые системы: издания по информационным технологиям -
http://www.npstoik.ru/vio - Электронный альманах «Вопросы информатизации образования» -
http://www.labirint.ru/ - Магазин книг -
http://www.edu.ru/index.php?page_id=6 Федеральный портал Российское образование -
edu - "Российское образование" Федеральный портал -
edu.ru - ресурсы портала для общего образования -
schoolHYPERLINK "http://www.school.edu.ru/".HYPERLINK "http://www.school.edu.ru/"edu - "Российский общеобразовательный портал" -
fepo - "Федеральный Интернет-экзамен в сфере профессионального образования" -
allbest - "Союз образовательных сайтов" -
fipi ФИПИ - федеральный институт педагогических измерений -
edHYPERLINK "http://www.ed.gov.ru/".HYPERLINK "http://www.ed.gov.ru/"gov - "Федеральное агентство по образованию РФ". -
obrnadzorHYPERLINK "http://www.obrnadzor.gov.ru/".HYPERLINK "http://www.obrnadzor.gov.ru/"gov - "Федеральная служба по надзору в сфере образования и науки" -
monHYPERLINK "http://www.mon.gov.ru/".HYPERLINK "http://www.mon.gov.ru/"gov - Официальный сайт Министерства образования и науки Российской Федерации -
rostHYPERLINK "http://www.rost.ru/projects/education/education_main.shtml".HYPERLINK "http://www.rost.ru/projects/education/education_main.shtml"ruHYPERLINK "http://www.rost.ru/projects/education/education_main.shtml"/HYPERLINK "http://www.rost.ru/projects/education/education_main.shtml"projects - Национальный проект "Образование". -
windowHYPERLINK "http://window.edu.ru/window".HYPERLINK "http://window.edu.ru/window"eduHYPERLINK "http://window.edu.ru/window".HYPERLINK "http://window.edu.ru/window"ru - Единое окно доступа к образовательным ресурсам -
Портал "ВСЕОБУЧ" -
newseducationHYPERLINK "http://www.newseducation.ru/".HYPERLINK "http://www.newseducation.ru/"ru - "Большая перемена" -
vipschoolHYPERLINK "http://www.vipschool.ru/priem.php".HYPERLINK "http://www.vipschool.ru/priem.php"ru СУНЦ МГУ - Специализированный учебно-научный центр - школа имени А.Н. Колмогорова. -
rgsu.net - Российский Государственный Социальный Университет.
