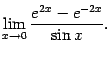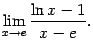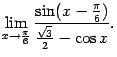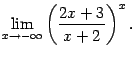Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Не указана

Добавлен: 28.03.2024

Просмотров: 321

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Знакомство с MathCad

Введение в MathCad

Переменные в выражениях Кроме чисел, в математических выражениях MathCad можно использовать переменные. При помощи переменных обозначаются скалярные величины, векторы, матрицы и функции. Имена переменных могут быть любой длины и состоять из латинских, греческих букв, цифр от 0 до 9, символа подчеркивания, %, . Переменная может быть набрана в любом шрифте, однако MathCad считает разными имена, набранные в разных регистрах и разными шрифтами, например, F, f, f  это разные переменные.Имя может начинаться с буквы или символа . Далее могут идти любые разрешенные символы, кроме . Если в имени используется символ “.”, то все символы, набранные после нее, представят нижний индекс имени, однако такие переменные не являются элементами массивов.Некоторые переменные в MathCad имеют предопределенные значения: , е, , %, TOL, ORIGIN, PRNCOLWIDTH, PRNPRECISION, FRAME, inn, outn.Пример. Выражение содержит две переменные: x и a.Переменные бывают локальными и глобальными.Присвоение значения локальной переменной записывается следующим образом:имя_переменной: = выражение(набираем имя_переменной : выражение), где выражение может быть либо числовым, либо содержать другие переменные.Примеры локальных переменных: Присвоение значения глобальной переменной записывается следующим образом:имя_переменной:  выражение(  набираем из палитры или при помощи символа “тильда”

Производные и их вычисление

Первообразная и ее нахождение

Матрицы и операции над ними

Задания

3. Найти транспонированные матрицы

5.Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

4. Найти обратные.

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5 . Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5 . Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

D=

5. Решить системы линейных уравнений методом Крамера.

Вариант №13

3. Найти транспонированные матрицы

5.Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

Вариант №18

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5.Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

Системы уравнений и их решение

Неравенства и их решение

Другие способы решения неравенств

Системы неравенств и их решение.

Последовательности и прогрессии.

Дифференциальные уравнения





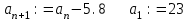
2) Теперь зададим дискретную переменную n. Проверим вначале первые 50 членов данной прогрессии:



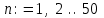
3
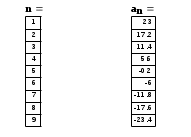
) Теперь выведем значения этих 50 членов прогрессии на экран:

Как мы видим число -122 является 26-м членом нашей прогрессии. Если бы среди этих 50 членов числа -122 не было бы, мы бы посмотрели на 50 член. Если он меньше -122, то в прогрессии вообще нет такого числа, иначе мы ищем дальше это число.

Задание 2. Определить, является ли число 2/27=0.0741 членом геометрической прогрессии 162; -54;…, и если является, то найти его номер.

Пример. Найти сумму первых десяти членов геометрической прогрессии (bn), в которой b1=3 и q=0,5.

Решение:

1) введем формулу данной геометрической прогрессии и начальные данные:



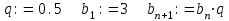
2) нажмем комбинацию клавиш [Ctrl]+[Shift]+[4]. Появится значок суммы. Кроме того, данный значок можно вызвать, щелкнув по нему в математической палитре.

Получим: 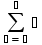— оператор суммы, где ■- пустые поля ввода.

3) теперь заполним соответствующие поля. В первом нижнем поле будет переменная n, которая является индексом нашей прогрессии, во втором нижнем поле - ее начальное значение, а в верхнем поле - конечное значение переменной n. В среднем поле под знаком суммы запишем n-й член нашей последовательности. Получим: .

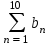4) нажав клавишу «=», получим ответ: =5.994.

Аналогичным образом можно посчитать и произведение членов любой последовательности и прогрессии. Операция произведения вызывается из палитры или комбинацией клавиш [Ctrl]+[Shift]+[3] и имеет следующий вид: 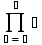, где ■ - поля ввода, такие же, как в операции суммирования.

Пределы

В пакете MathCad имеется возможность нахождения обычного, левостороннего и правостороннего пределов. Для этого существуют три оператора.


Пример. Найти .

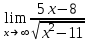Решение. Для решения данной задачи выполним последовательность таких действий:

  1. Нажимаем комбинацию клавиш [Ctrl]+[L] или щелкаем на панели математических знаков, на кнопке Calculus Toolbar для вызова оператора нахождения предела. На экране появится следующее:

  2. Ч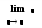
    ерные прямоугольники заполняем необходимыми данными.

П
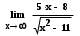
олучим:


  1. заключаем это выражение в выделяющую рамку;

  2. Нажимаем комбинацию клавиш [Shift]+[F9].

MathCad возвращает нам значение предела: 5. Если бы предела не существовало, MathCad возвратил бы сообщение “не определено”.

Задание 3.

Пример.

Вычислить 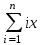. В символьном виде и для n=100 x=8

Набрать и нажать клавишу Enter



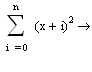
Получим





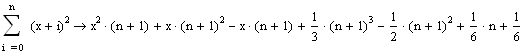
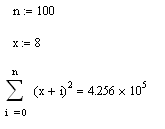
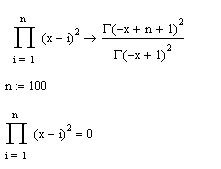
Аналогично вычисляется и произведение

Пример
Варианты заданий
n и х выбрать самостоятельно


  1. Вычислить .

  2. Вычислить .

  3. Вычислить .

  4. Вычислить .

  5. Вычислить .

  6. Вычислить .

  7. Вычислить .

  8. Вычислить .

  9. Вычислить

  10. Вычислить

  11. Вычислить .

  12. Вычислить

  1. Вычислить .

  2. Вычислить .

  3. Вычислить .

  4. Вычислить

  5. Вычислить .

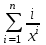  6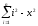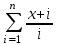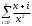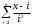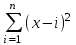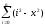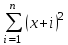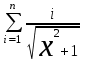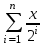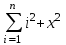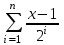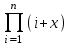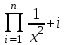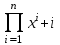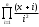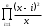. Вычислить .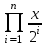

Задание 4.

Пример



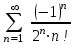
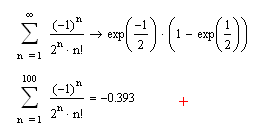
Набрать


Номер варианта
Общий член ряда

1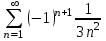


2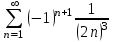


3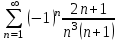


4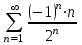


5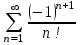


6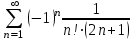


7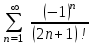


8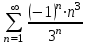


9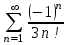


10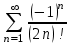


11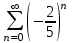


12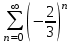


Задание 5.

Вычислить

Для вычисления предела щелкните по соответствующей позиции в панели Calculus; в помеченных позициях введите выражение допредельной функции и предельной точки; выделите все выражение и щелкните по кнопке Symbolic Evalution в панели символьных операций Symbolic; щелкните вне выделяющей рамки



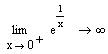
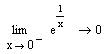
Варианты заданий












































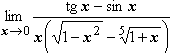
1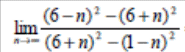


2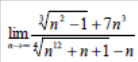


3


4


5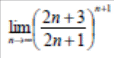


6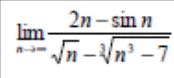


Контрольные вопросы

  1. Каким образом можно вычислить предел в Mathcad?

  2. Для чего необходимо задание операторов пользователя?

  3. Как задать оператор пользователя

Практитческая работа 10.

Дифференциальные уравнения

Цель работы: изучение методики решения дифференциальных уравнений в MathCad

Порядок выполнения работы:

  1. Выполнить тренировочные задания.

  2. Ответить на контрольные вопросы.

  3. Подготовить отчет о выполнении практической работы.

Смотрите также файлы