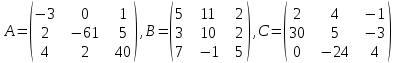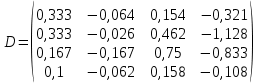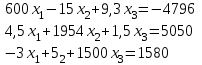Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx

Скачать файл (2,14Мб)

Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Не указана

Добавлен: 28.03.2024

Просмотров: 363

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Знакомство с MathCad

Введение в MathCad

Переменные в выражениях Кроме чисел, в математических выражениях MathCad можно использовать переменные. При помощи переменных обозначаются скалярные величины, векторы, матрицы и функции. Имена переменных могут быть любой длины и состоять из латинских, греческих букв, цифр от 0 до 9, символа подчеркивания, %, . Переменная может быть набрана в любом шрифте, однако MathCad считает разными имена, набранные в разных регистрах и разными шрифтами, например, F, f, f  это разные переменные.Имя может начинаться с буквы или символа . Далее могут идти любые разрешенные символы, кроме . Если в имени используется символ “.”, то все символы, набранные после нее, представят нижний индекс имени, однако такие переменные не являются элементами массивов.Некоторые переменные в MathCad имеют предопределенные значения: , е, , %, TOL, ORIGIN, PRNCOLWIDTH, PRNPRECISION, FRAME, inn, outn.Пример. Выражение содержит две переменные: x и a.Переменные бывают локальными и глобальными.Присвоение значения локальной переменной записывается следующим образом:имя_переменной: = выражение(набираем имя_переменной : выражение), где выражение может быть либо числовым, либо содержать другие переменные.Примеры локальных переменных: Присвоение значения глобальной переменной записывается следующим образом:имя_переменной:  выражение(  набираем из палитры или при помощи символа “тильда”

Производные и их вычисление

Первообразная и ее нахождение

Матрицы и операции над ними

Задания

3. Найти транспонированные матрицы

5.Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

4. Найти обратные.

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5 . Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5 . Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

Вариант №13

3. Найти транспонированные матрицы

5.Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

Вариант №18

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5.Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

3. Найти транспонированные матрицы

5. Решить системы линейных уравнений методом Крамера.

Системы уравнений и их решение

Неравенства и их решение

Другие способы решения неравенств

Системы неравенств и их решение.

Последовательности и прогрессии.

Дифференциальные уравнения

-5x₅=123

2x₁ + 9,6 x₂ +15,7x3+ 22x₄- 8x₅ =73

0,9 x₁+11,1x₂– 4,3x₃+ 1,5x₄+6,4 x₅=19

14x₁ + 45 x₂-38x₄+ 26x₅=49

220x₁ – 150x₂+ 3 x₃+95 x₅ =133

4x₁+ 6x₂- 14x₃ + 49x₅=65

21x₁ + 9 x₂- 2x₄- 12x₅= 58

110x₂- 60x₃+ 80x₄- 45x₅ = 290

5 x₂ + 27 x₃- 14x₄+ x₅ =72

87x₁ – 6,4x₂+ 130x₄ =140

Вариант №24

Вычислить определители

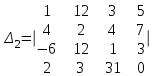
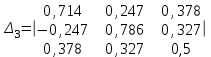
2. Найти произведение матриц АВ и ВА; CD и DC

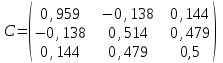
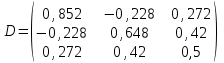
3. Найти транспонированные матрицы

4. Найти обратные матрицы.

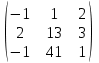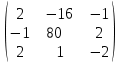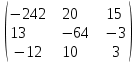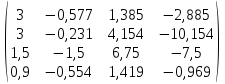5. Решить системы линейных уравнений методом Крамера.

-38 x₁ +60 x₂+ x₃+4 x₄+8x₅=65

18x₁ + 4x₂ +2x₃- 12x₅ =86

2x₂+ 19x₃- 7x₄+ 10x₅=130

0,4x₁ + 3x₂-4,2 x₃+ 2x₄- 5x₅=34

2,1x₁ + 13x₂- 20x₃+6 x₄ =18

₁+ х₂-2х₃ +2х₄= -2

3х₁+2х₂-2х₃ + х₄ = -6

7х₁+4х₂+2х₃+3х₄ = -6

2х₁-2х₂- х₃+ х₄ = 0

Вариант №25
1.Вычислить определители

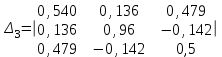
2. Найти произведение матриц АВ и ВА; CD и DC

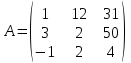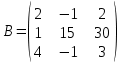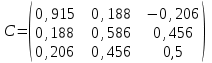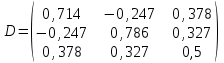3. Найти транспонированные матрицы

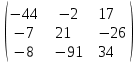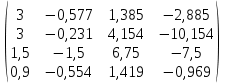4.Найти обратные матрицы.

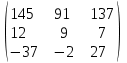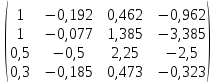5. Решить системы линейных уравнений методом Крамера.

0,5x₁-1,8x₃+9,2x₄+ 14x₅=120

9,6x₂-15,7x₃+24x₄- 8 x₅ = 74

0,8x₁ + 11,1x₂– 4,5x₃+1,5x₄-6,3 x₅=22

14x₁ + 45 x2 - 38x₄+ 26x₅ =46

220x₁- 148x₂-7 x₃+ 95x₅= 150
3

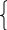х₁- 5х₂ + 3х₃= 46

х₁+ 2х₂ + х₃= 8

х₁- 7х₂ - 2х₃= 5

Вариант №26
1.Вычислить определители

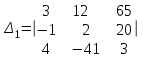
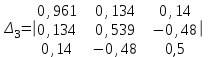
2. Найти произведение матриц АВ и ВА; CD и DC

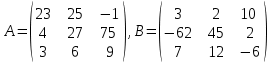
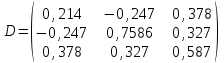
3. Найти транспонированные матрицы

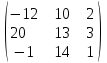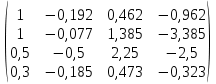4. Найти обратные матрицы и применить форматирование, чтобы элементы матрицы представляли собой правильные дроби.

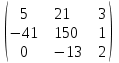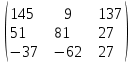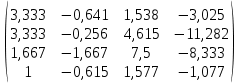5. Решить системы линейных уравнений методом Крамера.

₁+ х₂ + х₃+ х₄+ х₅= 72 -х₁-2х₂-4х₃= 421

3х₁+2х₂- х₃+ х₄-3х₅= -22 2х₁+ 3х₂+5х₃= 152

х₂+2х₃-2х₄+6х₅=23 х₁- х₂- х₃= -2

5х₁+4х₂+3х₃+3х₄- х₅=12

-х₂+12х₃+2х₄+6х₅=223

Контрольные вопросы

Перечислите основые матричные фунции.
Какие уравнения называются матричными?
Как решать матричные уравнения? Назовите способы решения матричных уравнений.

Практитческая работа 6.

Решение уравнений в MathCAD.
Цель работы: приобретение практических навыков решения уравнений в MathCAD.

В некоторых случаях для решения уравнений удобнее обратиться к встроенным возможностям решения уравнений пакета MathCad. В пакете имеется два способа решения уравнений: численный (по начальному приближению) и символьный, когда MathCad полностью всю работу берет на себя. Сначала рассмотрим первый способ.

I. Для решения уравнения с одной неизвестной используется функция root(f(x),x), которая возвращает значение x, при котором выражение или функция f(x) обращается в нуль.

Пример. Решить уравнение

Решение. Для решения этого уравнения необходимо выполнить следующие шаги:

1) приведем данное уравнение к такому виду, чтобы в правой части равенства был ноль:

.

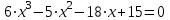2) введем какое-либо обозначение выражения в левой части уравнения. Например, создадим такую функцию:

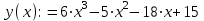
3) получаем, что для решения данного уравнения нам нужно найти все точки, в которых наша функция принимает нулевые значения, т.е. все x, при которых y(x)=0. Так как это уравнение третьей степени, то у него должны быть три корня (не обязательно разных). Для того, чтобы приблизительно определить эти корни, построим график функции y(x).

Пусть

Строим график, пользуясь пунктом Graph | X-Y Plot меню Insert.

4) MathCad не может высчитать нам все три корня сразу. Чтобы он высчитал один из корней, нам нужно подсказать ему приблизительное значение этого корня. Корни нашего уравнения - абсциссы точек пересечения графика нашей функции f(x) с осью OX. Возьмем самую левую точку пересечения. Ее абсцисса примерно равна -2. Записываем:

.

После того, как мы ввели «=», MathCad уточнил наше приближение и нашел ближайший к приближению корень. Аналогично для остальных двух корней:

Таким образом, найдены все три корня.

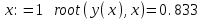
Ответ: -1,732; 0,833; 1,732

Задание 1. Найти решения уравнений:

а)

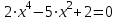; б)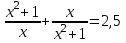

.

II. При решении уравнения вторым способом MathCad всю работу берет на себя. Рассмотрим решение уравнений этим способом на следующем примере.

Пример.