Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 342
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
Другие способы решения неравенств
Для решения неравенств существует два различных метода. Первый метод - метод интервалов (полностью соответствующий стандартному математическому методу интервалов). Второй метод - MathCad берет на себя всю работу по решению неравенства. Рассмотрим оба эти случая.
I. Метод интервалов.
Пример. Решить неравенство:
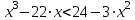 .
.Решение (по шагам):
1) приводим неравенство к такому виду, чтобы справа стоял ноль:
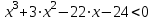 ;
;2) с помощью одного из изученных методов решаем уравнение
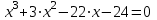 . Например, так:
. Например, так:• вводим уравнение;
• выделяем переменную
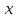 ;
;• вызываем пункт Variable | Solve меню Symbolics.
Получаем ответы: -6; -1; 4
3) задаем функцию
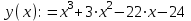 ;
;4) на каждом из интервалов
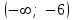 ,
, 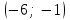 ,
, 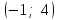 ,
, 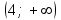 определяем знак функции:
определяем знак функции: 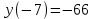
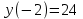
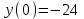
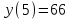 .
.Ответ: решение неравенства (-∞,-6)U(-1,4).
Примечание. Для ввода знаков отношений «», «≥», «≤», «» необходимо пользоваться комбинациями клавиш [Ctrl]+[=], [Ctrl]+[0], [Ctrl]+[9], [Ctrl]+[3] соответственно.
Задание 1. Методом интервалов решить следующие неравенства:
а)
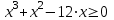 , б)
, б) 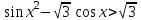 .
.II. Cледующий метод - уникальный метод пакета MathCad. Пакет MathCad сам, без участия человека, решает нужное неравенство.
Пример. Решить неравенство
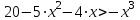 .
.Решение. Для решения данного неравенства нам необходимо осуществить следующую последовательность шагов:
1) ввести неравенство:
 ;
;2) щелчком мыши выделить в этом неравенстве переменную, относительно которой оно будет решаться. В нашем случае это переменная x;
3) вызвать пункт Variable | Solve меню Symbolics.
MathCad выдаст ответ в следующем виде
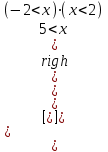
Первое выражение означает, что x<2 и -2
Второе означает, что x>5, т.е. решением неравенства будет следующее: x(-2,2)U(5,∞).
Задание 1. Решить следующие неравенства:
а)
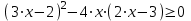 ; б)
; б)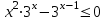 .
.П
 римечание. Для решения неравенств можно использовать функцию solve на панели инструментов Symbolic. Для этого вводим неравенство, и выбираем на панели Symbolic функцию solve
римечание. Для решения неравенств можно использовать функцию solve на панели инструментов Symbolic. Для этого вводим неравенство, и выбираем на панели Symbolic функцию solve 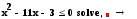
Затем в свободный шаблон введём имя переменной, относительно которой решаем неравенство (в нашем случае это x) и получим ответ
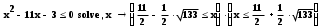 Знак умножения в ответе означает пересечение промежутков, а промежутки, записанные в одной паре скобок, объединяются. Например:
Знак умножения в ответе означает пересечение промежутков, а промежутки, записанные в одной паре скобок, объединяются. Например: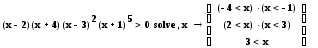
означает, что
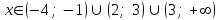 .
.Системы неравенств и их решение.
Пакет MathCad не имеет собственных средств для решения систем неравенств. Но можно воспользоваться тем, что он может решать отдельные неравенства в символьном виде. Рассмотрим на примере, как можно решить систему неравенств, используя решение отдельных неравенств системы.
Пример. Решить систему неравенств:
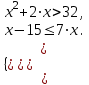
Решение. Решение данной системы будем осуществлять следующим образом:
1) введем оба неравенства, входящие в систему;
2) щелкнем по переменной первого неравенства (по x) в самом неравенстве;
3) вызовем пункт Variable | Solve меню Symbolics. Пакет MathCad выдаст на экран решение первого неравенства относительно переменной x. Это будет столбец:
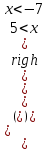 ;
;4) аналогичным образом, решив второе неравенство, получим следующий ответ:
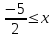 ;
;5) из полученных ответов мы можем, нарисовав рисунок, либо логически, определить, что решением системы будет x>5.
Задание 2. Решить системы неравенств:
а)
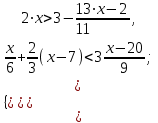 б)
б) 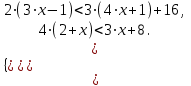
в)
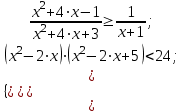 г)
г) 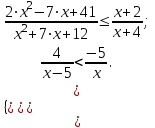
Задание 3.
Решить систему нелинейных уравнений с использованием вычислительного блока Given, Find. Преобразовать нелинейные уравнения к виду f1(x)=y и f2(y)=x. Построить их графики и определить начальное приближенное решение. Решить систему нелинейных уравнений с помощью функции Minerr.
-
 sin(x+1)+y=0,8
sin(x+1)+y=0,8Sin(y-1)+x=1,3
Решение.
-
Задаем начальный интервал поиска решений -
Определяем функцию y(x), строим ее график -
Находим приближенные корни
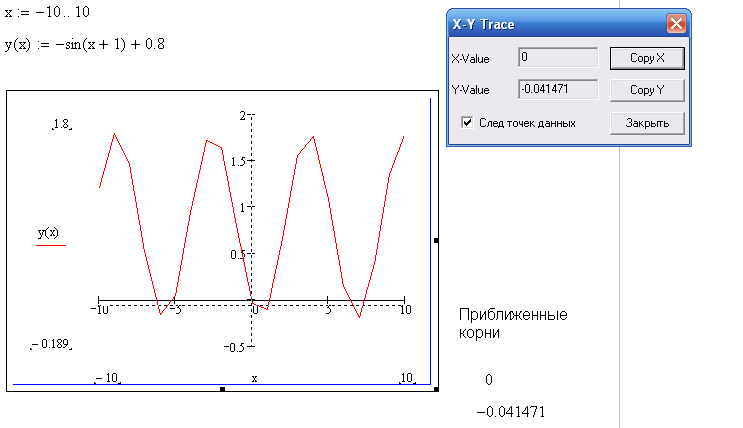
-
Определяем функцию x(y), строим ее график -
Находим приближенные корни
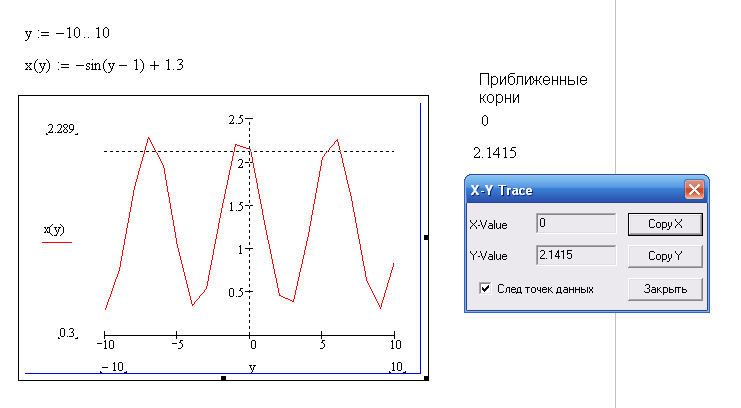
-
Записываем начальные приближения и решаем систему
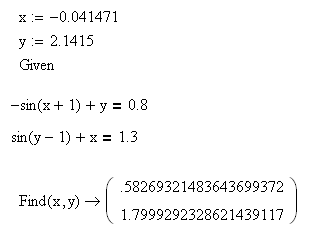
-
Делаем тоже самое с использованием функции minerr.
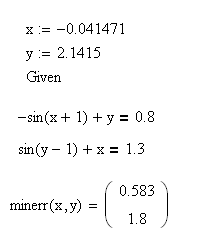
-
Делаем проверку
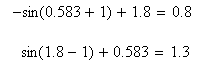
Варианты заданий

Контрольные вопросы
-
Дайте сравнительную характеристику функциям Find и Minerr. -
Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме? -
Перечислите символьные операции с выделенными выражениями. -
Перечислите символьные операции с выделенными переменными. -
Практитческая работа 9
Ряды и пределы в MathCAD
Цель работы: Получение наввычисления рядов и пределов в MathCAD.
Порядок выполнения
-
Выполнить тренировочные задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы.
Справочные сведения
2>
Последовательности и прогрессии.
С помощью пакета MathCad можно работать с различными последовательностями, производя различные операции над их членами, такие, например, как нахождение их суммы, произведения.
Пример. Найти первые 10 членов последовательности, заданной формулой n-ого члена
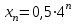 .
.Решение. Очевидно, что решение данной задачи довольно простое, но требует очень большого объема вычислений при расчете вручную. С помощью же MathCad в решении нет ничего сложного.
1) Зададим общий член нашей последовательности (чтобы ввести нижний индекс, необходимо сначала нажать клавишу «[»). Получим:
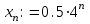 .
.2) Так как нам нужно узнать первые 10 членов данной последовательности, то n должно изменяться от 1 до 10 с шагом 1. Зададим соответствующую дискретную переменную:
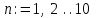 .
.3
 ) Теперь осталось вывести на экран значение xn, и задача решена:
) Теперь осталось вывести на экран значение xn, и задача решена:Аналогично можно рассчитать любое количество членов произвольных последовательностей.
Задание 1. Найти первые 8 членов следующих последовательностей:
а)
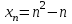 ; б)
; б) 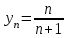 .
.В вышеприведенных примерах мы задавали последовательности в виде формулы n-го члена. Но можно также задавать последовательность посредством рекуррентной формулы, т. е. в виде закона, по которому член этой последовательности выражается через предыдущий(е) член(ы) последовательности. В частности, такими формулами задаются геометрические и арифметические прогрессии.
Пример. Проверить, является ли число -122 членом арифметической прогрессии 23;17.2;… и если является, то каким ?
Решение.
1) По определению арифметической прогрессия записывается рекуррентной формулой an+1 = an + d. В нашем случае d =17.2-23 = -5.8; a1=23. Введем полученную формулу и начальные данные:
