Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 346
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
10.

11.

Контрольные вопросы:
-
Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме? -
Перечислите символьные операции с выделенными выражениями. -
Перечислите символьные операции с выделенными переменными. -
Перечислите символьные операции преобразования. -
Какие параметры определяет стиль представления результатов вычислений и где он задается? -
В каких случаях результат символьных преобразований помещается в буфер обмена?
Практитческая работа 4.
Вычисление интегралов в MathCAD.
Цель работы: приобретение практических навыков вычисления интегралов в MathCAD.
Порядок выполнения работы:
-
Выполнить задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы
Первообразная и ее нахождение
Пакет MathCad имеет развитые средства для нахождения первообразных различных функций. С его помощью можно быстро и правильно найти первообразные большинства функций.
Пример. Найти одну из первообразных для каждой из следующих функций:
а)
 ; б)
; б)  .
.Решение.
-
нажмем комбинацию клавиш [Ctrl]+[ I ] или щелкаем на панели математических знаков на кнопке Calculus Toolbar, чтобы вызвать знак неопределенного интеграла (для нахождения одной из первообразных). Получим: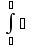
-
заполняем черные прямоугольники необходимыми данными. -
заключаем выражение в выделяющую рамку. -
нажимаем [Shift]+[F9].
Аналогичным образом решается пункт б) примера.
Задание 1. Найти первообразные следующих функций и провести проверку на правильность ответа, т.е. найти производную от полученных функций:
а)
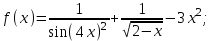
б)
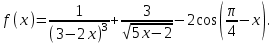
Первообразную в MathCad можно найти и несколько другим способом. Этот способ позволяет, не вводя операцию нахождения интеграла, вычислить значение одной из первообразных функций.
Пример. Найти первообразную следующей функции:
 .
.Решение.
-
введем функцию; -
щелчком мыши выделим переменную интегрирования х; -
из меню Symbolics выбираем пункт Variable, а затем Integrate.
MathCad отобразит результат интегрирования.
Порядок выполнения работы:
Изучение элементы пользовательского интерфейса MathCAD.
-
Выполнить задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы
Задание 1.
Проинтегрировать заданную функцию и построить графики заданной функции и ее первообразной
Пример.
Исходное выражение

Решение
Записываем выражение функции

-
Выделить курсором переменную х и в главном меню выбрать Symboliecs/Variadle/Integrate.
На экране появится:

-
Записать:

-
Построить графики: Кнопка . В шаблоне ввести в нижней части х, сбоку через запятую у(х), у1(х)
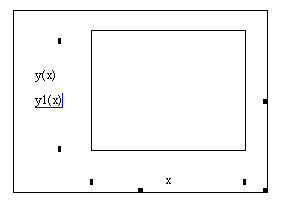
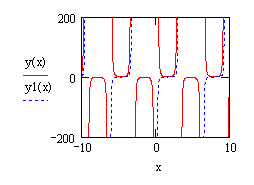
Щелкнуть в центр шаблона. Получим графики.
Варианты заданий.
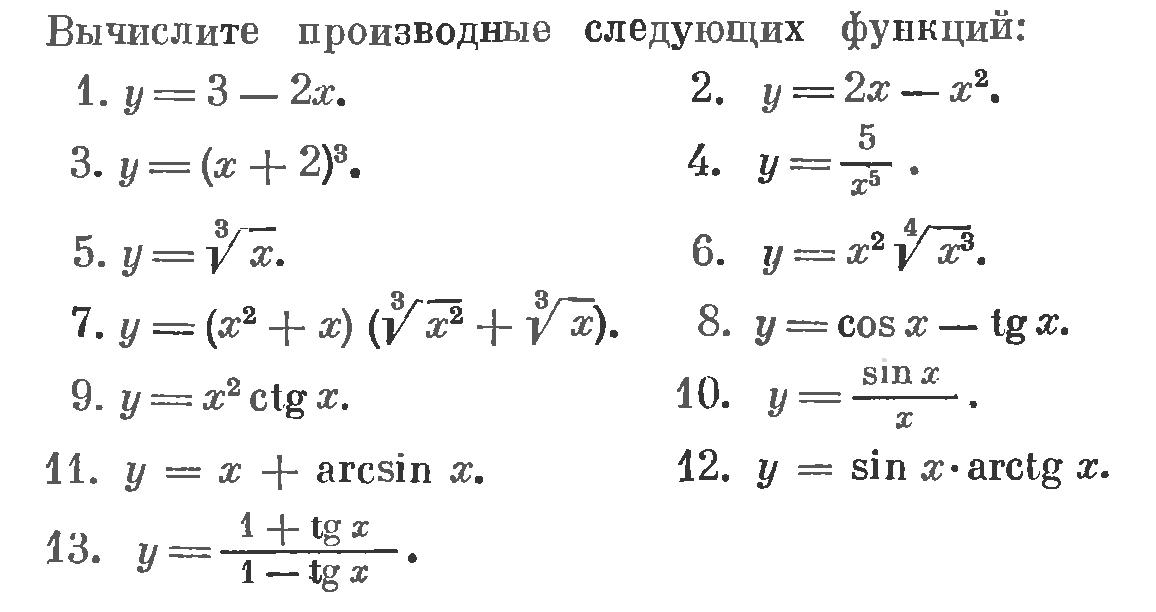
Задание 2.
Найти определенный интеграл.
Пример.

С помощью шаблона определенного интеграла набрать:
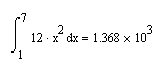
Варианты заданий
| 1 |  |
| 2 |  |
| 3 | 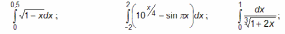 |
| 4 |  |
| 5 | 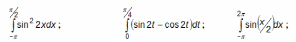 |
| 6 | 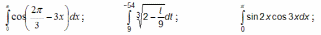 |
| 7 |    |
| 8 |  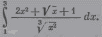 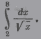 |
| 9 |  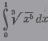 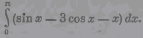 |
| 10 |    |
| 11 | 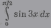   |
| 12 | 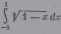   |
Контрольные вопросы:
-
Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме? -
Перечислите символьные операции с выделенными выражениями. -
Перечислите символьные операции с выделенными переменными. -
Перечислите символьные операции преобразования. -
Какие параметры определяет стиль представления результатов вычислений и где он задается? -
В каких случаях результат символьных преобразований помещается в буфер обмена?
Практитческая работа 5.
Матричные вычисления
Цель работы: приобретение практических навыков выполнения основных операций с матрицами в MathCAD.
Порядок выполнения работы:
-
Выполнить задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы
Матрицы и операции над ними
С помощью пакета MathCad можно эффективно работать с разнообразными матрицами, быстро и качественно проводя над ними довольно трудоемкие операции.
Создается матрица следующим образом:
-
щелкаем мышкой на нужном месте рабочего документа; -
щелкаем на панели математических знаков на кнопке Vector and MatrixToolbar, выбираем кнопку Vector or Matrix; -
в появившемся диалоговом окне вводим необходимое нам количество строк и столбцов и щелкаем на кнопке “OK”. Получаем следующее (для матрицы размерностью 3*3):
передвигая курсор по матрице, заполняем соответствующие поля. В итоге получим требуемую матрицу.
Для изменения размеров матрицы нужно:
-
щелкнуть на элементе матрицы, от позиции которого будут осуществляться изменения; -
снова щелкаем на панели математических знаков, на кнопке Vector and MatrixToolbar, выбираем кнопку Vector or Matrix, задать нужное число столбцов и строк и выбрать кнопку Insert либо Delete.
Пример. Дана матрица:

Выделим элемент А(2,2) данной матрицы и удалим одну строку и один столбец.
Получим матрицу:
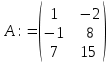
Теперь рассмотрим операции над матрицами:
Пусть даны матрицы:
Операции, которые можно задавать через палитру:
-
А+В – сумма матриц, -
А*В – произведение матриц, -

A= -12 - определитель матрицы,
| 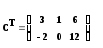 |
|  |
| 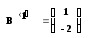 |
Матричные функции:
-
max(С) – наибольший элемент матрицы. -
min(С) – наименьший элемент матрицы. -
tr(B) – след матрицы. -
rank(A) — ранг матрицы. -
eigenvals(M) – собственные значения матрицы. -
eigenvecs(M) – собственные векторы матрицы. -
norm1(M), norm2(M), norme(M), normi(M) — различные нормы квадратной матрицы -
cond1(M), cond2(M), conde(M), condi(M) — число обусловленности матрицы, основанное на различных нормах.
