Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 347
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
Системы уравнений и их решение
MathCad дает возможность решать не только одиночные уравнения, но и системы уравнений. Максимальное число уравнений и переменных в системе должно быть равно пятидесяти. Как и для решения одного уравнения, существуют два способа решения систем уравнений: численный (по начальному приближению) и символьный (всю работу делает MathCad). Рассмотрим оба метода.
I. Численное решение систем уравнений.
Пример. Решить систему уравнений:
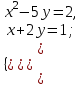
Решение. Сначала решим данную систему обычным графическим методом (приближенно):
-
Выразим из каждого уравнения системы переменную у. Получим эквивалентную систему: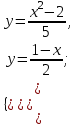
-
Построим графики двух этих функций; -
По рисунку приблизительно оценим абсциссы и ординаты точек пересечения графиков наших функций. В нашем случае это будут примерно точки: (-3.7; 2.4) и (1; 0).
Полученные нами приближения очень грубы, и поэтому продолжим решение этой системы, позволив MathCad уточнить их;
-
Зададим начальные приближения (-3.7; 2.4) для переменных х и у.
х:=-3.7 у:=2.4;
-
Напечатаем английское слово Given. Оно дает знать пакету MathCad, что далее следует система уравнений; -
Введем в любом порядке наши уравнения. Для набора знака “равно” нужно использовать комбинацию клавиш [Ctrl]+[=] или щелкаем на панели математических знаков на кнопке “Boolean Toolbar” и выбираем особый (жирный) знак равенства; -
Присвоим какой-либо переменной значение функции Find(х,у).
а:=Find(x,y)
Данная функция находит решение введенной выше системы уравнений. В круглых скобках должны быть перечислены все неизвестные указанной системы.
-
запрашиваем у MathCad ответ:
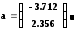
В ответ на наше начальное приближение мы получили уточненное решение системы уравнений.
Аналогичным образом получаем уточнение и для второго приближения.
Задание 1. Решить системы уравнений:
а)
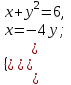 б)
б) 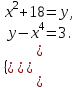
При решении систем уравнений с двумя неизвестными мы еще можем получить начальные приближения по графику. Для систем же с тремя и более неизвестными это становится почти невозможно. Также этим способом трудно решать системы с большим количеством различных функций. В этих случаях можно использовать второй способ решения систем уравнений.
II. Символьное решение систем уравнений.
Пример. Решить систему уравнений:
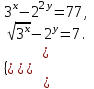
Решение. Будем решать эту систему следующим образом:
-
набираем ключевое слово Given; -
вводим наши уравнения (для ввода знака “=” используется комбинация [Ctrl]+[=]); -
печатаем функцию Find(x,y); -
нажимаем комбинацию клавиш [Ctrl]+[.] или щелкаем на панели математических знаков на кнопке Evaluation Toolbar и выбираем значок “” – это символьный знак равенства. -
Нажимаем ввод.
M
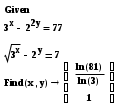
athCad выдаст решение введенной системы.
Задание 1.
Решение линейных и нелинейных систем уравнений.
Пример.
Решить систему уравнений
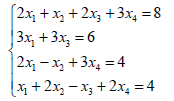
Набрать :

Варианты заданий:
| 1 | 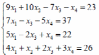 | 7 | 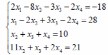 |
| 2 | 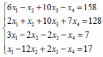 | 8 | 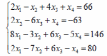 |
| 3 | 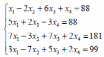 | 9 | 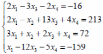 |
| 4 | 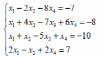 | 10 |  |
| 5 | 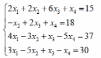 | 11 | 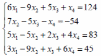 |
| 6 | 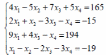 | 12 | 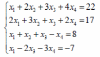 |
Контрольные вопросы:
-
Как символьно решить уравнение или систему уравнений в Mathcad? -
Какой знак равенства используется? -
Какой комбинацией клавиш вставляется в документ? -
Назовите особенности использования символьного решения уравнений. -
Назовите способы выполнения символьных операций в Mathcad. -
Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме?
Практитческая работа 8.
Решение неравенств в MathCAD.
Цель работы: освоение методики решения неравенств в MathCAD.
Порядок выполнения работы:
-
Освоить решения неравенств в MathCAD. -
Выполнить задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы.
Общие сведения.
Неравенства и их решение
Решить неравенство с использованием MathCad можно разными способами. Можно описать пакету MathCad тот или иной способ решения неравенства, и решать их в соответствии с нашим описанием. Можно также всю работу поручить самому пакету: пусть он решает неравенство собственным способом.
Одним из наиболее употребимых методов решения неравенств является метод интервалов. Как известно, данный метод состоит из следующих двух основных шагов:
-
решение уравнения типа w=0, соответствующего неравенству, где w – выражение, полученное приведением неравенства к виду, когда с одной стороны от знака сравнения стоит некоторое выражение, а с другой – нуль; -
оценка знака выражения w на каждом из полученных интервалов.
Первый из этих пунктов очень просто решается с помощью методов, рассмотренных нами в предыдущих занятиях. А вот как поступить со вторым пунктом, рассмотрим на следующем примере.
Пример. Решить неравенства:
а) 5x2 - 12х > 6; б) x2 – 10х-3 x.
Решение. Мы видим, что неравенства приводятся к одному общему виду: a x2 + b x +c ? 0, где a, b, c – некоторые коэффициенты, а знак “?” заменяет любой из знаков “”,””,””,””. Поэтому достаточно решить неравенство в общем виде, а затем, меняя коэффициенты, получим решение любого неравенства такого типа. Решать неравенство в общем виде будем следующим образом:
-
необходимо решить уравнение ax2 + bx +c=0 в общем виде. Для этого воспользуемся уже написанной нами программой KVAD(a,b,c). Она имеет вид:
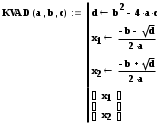
-
необходимо определить знаки выражения ax2 + bx +c на каждом из трех промежутков (-, х1),( х1, х2),( х2, ). Для этого можно написать программу, которая по заданным значениям корней вычисляет знаки на трех полученных промежутках. Но мы не будем писать для этого отдельную программу, а напишем общую программу решения неравенств данного типа KNER(a,b,c), которая будет использовать программу KVAD(a,b,c) для поиска корней уравнения, а затем определять знаки выражения на получившихся интервалах.
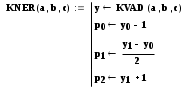
-
теперь мы должны найти значение выражения ax2 + bx +c в каждой из точек рi. В программах MathCad имеется возможность определенное число раз повторить одинаковый набор операций для разных данных. Это реализуется посредством цикла. В нашем случае получим, воспользовавшись для ввода цикла кнопкой “for” палитры программирования и заполнив поля вода, следующее:
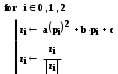
Здесь для каждой из трех точек мы вычислили значение zi выражения a x2 + b x +c. Кроме того, второй операцией мы разделили значение zi на его модуль, получив в итоге: -1, если zi отрицательное, 1 – если zi положительное. Эти две операции мы выполнили в цикле, так как они стоят за вертикальной чертой цикла.
Теперь у нас имеется все, что нужно: - два корня y0 и y1, а также знаки zi на каждом из трех интервалов. Выдадим их значения в виде столбца, воспользовавшись пунктом Matrix меню Insert для вызова, и заполнив столбцы необходимыми значениями. В итоге получим следующую программу:
Программа решения неравенств вида a x2 + b x +c ? 0, где ? – один из знаков , , , , методом интервалов.
Ответ выдается в виде столбца, где сначала расположены корни уравнения a x2 + b x +c = 0, а затем знаки a x2 + b x +c на трех интервалах в порядке слева направо.
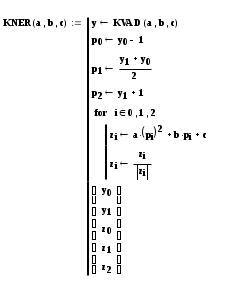
Т
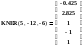 аким образом, теперь мы имеем возможность, решить любое неравенство данного вида.
аким образом, теперь мы имеем возможность, решить любое неравенство данного вида.Решим заданные неравенства.
а) 5x2 - 12х > 6; 5x2 - 12х - 6 > 0;
Вызовем нашу программу:
О
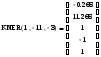 тсюда видно, что решением неравенства являются интервалы (‑,-4.248)(2.825,+);
тсюда видно, что решением неравенства являются интервалы (‑,-4.248)(2.825,+);б) x2 - 10х – 3 х; x2 - 11х – 3 0.
Вызываем программу:
Итого, решением нашего неравенства будет отрезок: [-0.266; 11.266]
Аналогичные программы мы можем написать и для решения других типов неравенств.
