Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 369
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
С клавиатуры можно ввести не все математические операции. Любую математическую операцию, известную MathCad, можно ввести с помощью одной из палитр. Наиболее часто используемые операции находятся на палитре с изображением калькулятора. Вводятся они щелчком мыши по значку нужной операции.
Основные правила редактирования выражений
-
Включение/выключение режима вставки – достигается клавишей Ins; -
Изменение направления ввода - достигается клавишей Ins или клавишами и ; -
Перемещение курсора ввода - достигается клавишами и ; -
Расширение курсора ввода - достигается клавишей ПРОБЕЛ; -
Вставка оператора - достигается установкой курсора между операндами и ввода символа оператора; -
Вставка оператора после части выражения - достигается выделением части выражения и затем ввода оператора; -
Вставка квадратного корня - достигается выделением курсором ввода подкоренного выражения и затем ввода знака \; -
Вставка унарного минуса - достигается выделением фрагмента выражения, перед которым вставляется минус, нажатием клавиши Ins, а затем клавиши минус; -
Удаление оператора - достигается установкой курсора ввода после оператора и нажатием клавиши Backspase; -
Освобождение выражения от скобок - достигается установкой курсора ввода справа от открывающей скобки и нажатием клавиши Del (или слева и клавишей Backspase); -
Вставка фрагмента выражения в скобки – достигается охватом выражения курсором ввода и набором символа одиночной кавычки; -
Задание выражения в качестве аргумента функции – достигается охватом курсором ввода выражения, вводом скобок, расширением курсора ввода для охвата всего выражения со скобками и вводом имени функции (например, с применением кнопки на панели инструментов); -
Отказ от неверно проделанной операции – достигается выбором команды Undo в меню Edit или щелчком на кнопке Undo на панели инструментов.
Переменные в выражениях
Кроме чисел, в математических выражениях MathCad можно использовать переменные. При помощи переменных обозначаются скалярные величины, векторы, матрицы и функции. Имена переменных могут быть любой длины и состоять из латинских, греческих букв, цифр от 0 до 9, символа подчеркивания, %, . Переменная может быть набрана в любом шрифте, однако MathCad считает разными имена, набранные в разных регистрах и разными шрифтами, например, F, f, f это разные переменные.
Имя может начинаться с буквы или символа . Далее могут идти любые разрешенные символы, кроме . Если в имени используется символ “.”, то все символы, набранные после нее, представят нижний индекс имени, однако такие переменные не являются элементами массивов.
Некоторые переменные в MathCad имеют предопределенные значения: , е, , %, TOL, ORIGIN, PRNCOLWIDTH, PRNPRECISION, FRAME, inn, outn.
Пример. Выражение  содержит две переменные: x и a.
содержит две переменные: x и a.
Переменные бывают локальными и глобальными.
Присвоение значения локальной переменной записывается следующим образом:
имя_переменной: = выражение
(набираем имя_переменной : выражение),
где выражение может быть либо числовым, либо содержать другие переменные.
Примеры локальных переменных:
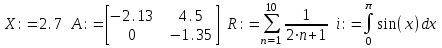
Присвоение значения глобальной переменной записывается следующим образом:
имя_переменной: выражение
( набираем из палитры или при помощи символа “тильда”
).Примеры глобальных переменных:
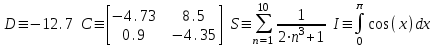
MathCad читает рабочий документ сверху вниз и слева направо. При первом просмотре глобальные переменные инициализируются и им присваиваются начальные значения, при втором просмотре значения присваиваются локальным переменным. Определив переменную, ее можно использовать при подсчетах ниже и правее. Когда какой-то переменной не присвоено значение, тогда в выражении она будет отражена другим цветом. Переменные можно использовать далее и с переопределенными значениями.
Если некоторые вычисления надо пометить комментариями, тогда открывают текстовую область, например, при помощи Insert - вставки текста. В простейшем случае для ввода текста достаточно ввести символ одной двойной кавычки — «“». В появившемся прямоугольнике можно начинать вводить текст. В текстовой области курсор ввода имеет вид красной вертикальной черты и отмечает место ввода. Текст редактируется общепринятыми средствами. Нажатие клавиши
Enter осуществляет переход к новой строке, а Shift + Enter — выход из текстовой области.
Примечание. В следующем примере вам нужно будет задать переменную с определенной единицей измерения. Это можно сделать с помощью пункта Unit из меню Insert. Команда Unit (единицы) служит для задания единиц измерения размерных величин. Размерные величины широко используются в физических и научно-технических расчетах.
При выборе команды Unit появляется диалоговое окно со списком размерных величин (Dimension) и относящихся к ним единиц измерения (Unit). В поле System отображается текущая система единиц измерения. По умолчанию используется система SI.
Пример. Найти площадь S прямоугольника ABCD, если известно: AB=15 cm, BC=13,7 cm;
Решение.
В
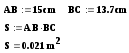
данном примере мы определили переменную S через переменные AB и BC. Если мы изменим значения переменных AB и BC, то изменится и значение площади S.
Задание 1. Даны три точки А(2; 5), В(-6; 8), С(13; 6). Пользуясь формулой Герона
 , где р – полупериметр треугольника ABC, a, b, c – длины его сторон, найти его площадь.
, где р – полупериметр треугольника ABC, a, b, c – длины его сторон, найти его площадь.В математике часто встречаются задачи, в которых какое-нибудь выражение зависит от переменной, а переменная принимает не одно, а набор значений, и для каждого из этих значений нужно узнать значение выражения. На этот случай в MathCad существуют так называемые дискретные переменные (их еще называют ранжированными). Они определяются так:
имя_переменной:= нач_знач, след_знач .. посл_знач
(набираем:
имя_переменной : нач_знач , след_знач ; посл_знач)
Например, t: =10, 11.. 17 означает, что переменная t принимает значения от 10 до 17 с шагом 1, т.е. 10, 11, 12, 13, 14, 15, 16, 17. Рассмотрим задачу, использующую дискретные переменные.
На первый взгляд дискретная переменная напоминает вектор – одномерный массив индексированных переменных. Но это далеко не так. Это просто связанная с переменной совокупность значений.
Для задания векторов и матриц также можно использовать дискретные переменные, которые принимают значения изменения индекса. Индексы могут начинаться с 0 или 1. Эти установки задает специальная системная переменная ORIGIN, имеющая по умолчанию значение 0. Вводить индексы можно или через палитру, или клавишей “[“. Пример получения значений вектора
x0, x1,…, x10:
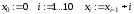
Пример. Построить таблицу значений функции:
 при x = -3, -2, -1, 0, 1.
при x = -3, -2, -1, 0, 1. Решение.
Е

сли выражение зависит от двух дискретных переменных, его значение будет выведено в виде прямоугольной таблицы, например, как в следующем случае:
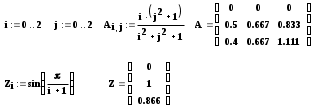
Задание 1.
Вычислить значение функции при заданном значении аргумента.
Пример:

Задания
| Вариант | Функция | Аргументы |
| 1 | | 7; -8; 1,2; 64; -15,8 |
| 2 | | 9; 0,5; 7,6; -95; 4,1 |
| 3 | | 0,2; 45; -789; 0,456; 56 |
| 4 | Y= 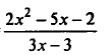 | 12,89; -458; 0,7895, 15555; -23,78 |
| 5 | Y= 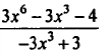 | 0,7; 89, -74; 23; 56 |
| 6 | Y=  | 1,89; 0,2567; 58,45; 56,789; 0,21 |
| 7 | | 56,789; 2345; -4567; 52,78; 74,56 |
| 8 | | 54,87; -1458; 78,56; 1278; -75,46 |
| 9 | | 56; 78; 2; -75; 78,23 |
| 10 | | 23,23; 45,45; 78,3; 49,123; -789 |
| 11 | 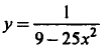 | 78; 96,12; -36,78; -0,256; 0,7516 |
| 12 | | 0,4789; 75; 56; -0,23; 0,23457 |
Задание 2
Выполнить вычисления с использованием стандартных функций:
Пример:
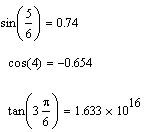
Задания
| Вариант | Функция | Функция |
| 1 | | |
| 2 | 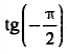 | |
| 3 |  | |
| 4 | 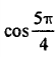  | |
| 5 | 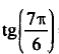 | |
| 6 | | |
| 7 | 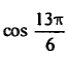 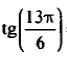 | 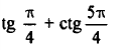 |
| 8 | 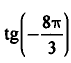 | |
| 9 | 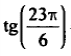 |  |
| 10 | 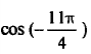 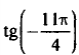 | |
| 11 | 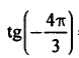 | 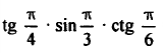 |
| 12 | 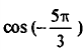 | |
