ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 565
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Вопросы для самопроверки и самоконтроля
Вопросы для самопроверки и самоконтроля
Вопросы для самопроверки и самоконтроля
Вопросы для самопроверки и самоконтроля
Вопросы для самопроверки и самоконтроля
Прибыль: П = 1044203 -766333 = 277870
Вопросы для самопроверки и самоконтроля
Вопросы для самопроверки и самоконтроля
i = (1235 + 1874 + + 1963) = 5074 тыс. руб. Вторая величина определяется следующим образом:
∑ Дi = 0 + 0 + 0 + 502 + 520 + ... + 600 + 600 = 9252 тыс. руб.
Простое сравнение двух полученных величин свидетельствует о том, что доходная составляющая больше инвестиционной (9252 > 5074). Наличие именно такого неравенства однозначно определяет внутреннюю норму доходности как величину больше нуля.
Если бы две сравниваемые величины точно совпали, то тогда искомый показатель был бы равен нулю. И наконец, в случае когда инвестиционная сумма больше доходной составляющей, искомый показатель внутренней нормы доходности представляет отрицательную величину. Но тогда инвестор, очевидно, откажется от такого проекта и примет к рассмотрению исследуемый проект лишь тогда, когда доходы предприятия будут больше инвестиций. Именно такой случай рассматривается в нашем примере. Поэтому можно перейти к дальнейшему анализу и определению величины внутренней нормы доходности.
Второй шаг. Устанавливают величину искомого показателя на определенном уровне. Предположим, что расчетчик примет показатель q = 0,1, после чего произведет расчеты инвестиционных вложений и доходной составляющей проекта с применением принятой нормы доходности по формуле 8.2. Тогда у него получится отрицательная величина, ибо сумма инвестиций окажется больше доходной составляющей проекта (читатель может сам убедиться в этом, произведя соответствующие расчеты). Такой результат будет свидетельствовать о том, что установленная эмпирическим путем величина внутренней нормы доходности должна быть в данном проекте меньше 0,1 и, следовательно, дальнейший поиск связан с некоторым уменьшением величины этого показателя. Обычно если выполнять расчет чисто механически, то можно для дальнейших расчетов принять среднее значение показателя между двумя соседними расчетами, т.е. в нашем примере это будет q = 0,05, поскольку этот результат и есть средняя между 0 и 0,1.
Приняв новое значение внутренней нормы доходности, переходят к новому шагу в проводимых расчетах.
Третий шаг. Все расчеты точно повторяются, но уже с нормой доходности q= 0,05. Опять-таки возможны два случая: либо разность между доходной и инвестиционной частями проекта больше, либо она меньше нуля. Если имеет, место последний случай, то надо уменьшать внутреннюю норму доходности (например, до величины q
= 0,025) и все расчеты повторить. Если окажется, что разность двух составляющих проекта будет положительной, т.е. больше нуля (именно так случится в нашем примере, если все расчеты произвести по аналогии с ранее выполняемыми), то значение принимаемой нормы доходности надо будет вновь увеличить, доведя ее до величины q= 0,075. Это значение будет достаточно близким к истинной величине искомой нормы доходности, которая была получена на уровне q= 0,0698 с помощью компьютерной технологии.
Подобные расчеты можно продолжать многократно до получения искомого результата с такой точностью, какая будет нужна инвестору. В конечном счете потребность в информации о величине внутренней нормы доходности проекта встречается не так часто, чтобы на точности расчетов экономить несколько часов операционной работы.
В заключение следует отметить, что показатель внутренней нормы доходности применяется очень широко на многих предприятиях и многими инвесторами. Но особенно важное значение этот показатель имеет для крупных производств, для масштабных проектов, при реализации которых оцениваются их стратегичность и растянутость жизненного цикла, в течение которого проект будет приносить большой доход.
8.2. Показатель чистого приведенного дохода,
область его применения и методика расчета
Конкретная производственно-хозяйственная и предпринимательская практика чрезвычайно разнообразны как по масштабам будущего нового дела, так и по характеру используемой технологии, планируемой организации производства, проектируемой системы управления. Кроме того, проекты могут существенно различаться по длительности жизненного цикла, по срокам инвестиционных платежей, величине и характеру поступления во времени доходов функционирующего бизнеса и т.п.
Поэтому, чтобы иметь возможность отразить все имеющееся разнообразие форм и результатов предпринимательского бизнеса при оценке его эффективности, необходимо иметь несколько показателей. Одним из таких показателей является показатель чистого приведенного дохода (в экономической литературе его называют также чистой приведенной стоимостью).
Показатель чистого приведенного дохода довольно широко применяется в экономике. При его исчислении нормативная величина дохода рассматривается как упущенная выгода и поэтому считается как бы дополнительно понесенными затратами. Все, что получено предпринимателем сверх общих затрат (основных и дополнительных) отражает чистый приведенный доход.
Чистый приведенный доход рассчитывается по формуле
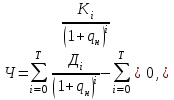(8.6)
где Ч — чистый приведенный доход за жизненный цикл проекта;
Дi _ величина дохода в i -ом временном интервале (формула 8.3);
Кi _ величина инвестиционных платежей в i -ом временном интервале (формула 8.4);
Т — количество временных интервалов в жизненном цикле проекта (длительность временного интервала заранее устанавливается, например месяц, два месяца, и т.д.);
qн — норматив дисконтирования затрат и результатов проекта на момент начала его жизненного цикла
qн = qг+ qс + qо, (8.7)
где qг ― гарантированная норма получения дивидендов на вложенный капитал в высоконадежном банке (в долях единицы);
qс — страховая норма, учитывающая риск вложений (в долях единицы), наличие и полноту страхования инвестиционной деятельности (если предприниматель вообще не страхует свою деятельность, то страховая норма принимается по максимуму; если страховка имеется, то страховая норма уменьшается в зависимости от полноты страхования вплоть до нуля);
qо — минимальная граница доходности проекта (в долях единицы), которая по мнению предпринимателя может его устроить и принимается им для себя самостоятельно.
Рассчитаем на конкретном примере чистый приведенный доход по исходным данным, представленным в табл. 8.1. Дополнительно примем норматив дисконтирования q = 0,06. Его величина складывается из следующих элементов: qг= 0,035; qc= 0,01; qо = 0,015.
Тогда после подстановки исходных данных в формулу 8.6 получим
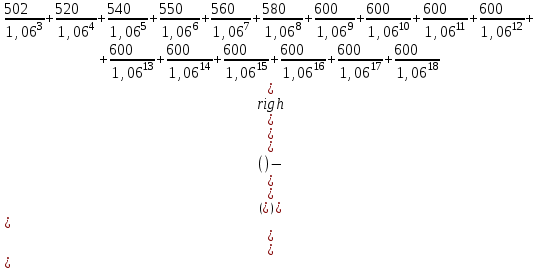
Таким образом, чистый приведенный доход составляет Ч = 381,72.
Как истолковать полученный результат? Прежде всего отметим, что на величину 381,72 денежных единиц проектируемый приведенный доход предприятия за жизненный цикл проекта превысит понесенные инвестором вложения. Это значит, что будущий доход предприятия полностью возместит осуществленные инвестиции и дополнительно обеспечит ему чистый доход в указанном размере. При этом в полученную сумму дохода не включаются упущенная выгода и страховка. Не учитывается в ней и заранее установленное ограничение в минимальном доходе. Все указанные элементы дохода также будут получены предприятием, но они гарантированы включенными в расчет нормативами. Поэтому подлинный доход предприятия будет значительно выше полученной расчетной суммы. Такова природа рассматриваемого показателя, который поэтому и называется чистым приведенным доходом. В нем подлинный доход от реализации проекта не показан, но, безусловно, подразумевается при оценке эффективности инвестиций и учитывается с помощью других показателей (например, при исчислении внутренней нормы доходности).
Проиллюстрируем экономический смысл показателя чистого приведенного дохода с помощью графика (рис. 8.1).
Вспомним, что в рассматриваемом примере показатель внутренней нормы доходности составляет q= 0,0698. Если норматив дисконтирования при расчете будет принят на уровне внутренней нормы доходности, т.е. равным 0,0698, то чистый приведенный доход в этом случае будет равен нулю. Это значит, что сверх установленного норматива предприятие никакого дохода не получит.
Теперь обратим внимание на горизонтальную линию с нулевым чистым приведенным доходом. Если норматив дисконтирования будет больше величины 0,0698, то чистый приведенный доход окажется величиной отрицательной и попадет на рассматриваемом графике в затемненную зону (например, при нормативе qн = 0,08).
Иная ситуация сложится, если норматив дисконтирования будет меньше величины внутренней нормы доходности (< 0,0698), т.е., как принято в рассматриваемом примере, q= 0,06. Тогда чистый приведенный доход будет больше нуля и составит величину Ч = 381,72.
Двигаясь влево к нулевой координате норматива дисконтирования, и тем самым снижая его величину, получим более высокий приведенный чистый доход, ибо движение к нулевому нормативу одновременно будет сопровождаться движением вверх по изображенной на графике кривой. При нулевой координате норматива дисконтирования чистый приведенный доход составит Ч = 4178 (разность между доходной составляющей проекта и величиной инвестиционных вложений без учета фактора времени, т.е. при qн = 0). По ранее произведенным расчетам (§ 8.1) эта разность получится, если (9252 5074) = 4178.
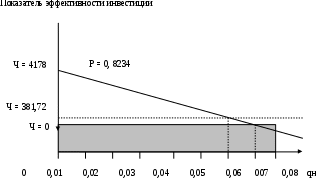Рис.8.1. Определение чистого приведенного дохода и рентабельности инвестиций
Таким образом, величина чистого приведенного дохода в огромной степени определяется не только объективными параметрами дохода предприятия и инвестициями в проект за его жизненный цикл, но и установленным нормативом дисконтирования. Если принятая норма окажется ошибочной, то будет иметь погрешность и величина чистого приведенного дохода. Поэтому при определении указанного норматива нужен тщательный анализ всей необходимой информации.
Рассматриваемый показатель достаточно широко распространен на предприятиях среднего бизнеса, реже он используется на предприятиях крупного и малого бизнеса, поскольку там главное внимание уделяется другим показателям. В частности, на крупных предприятиях предпочтение отдается показателю внутренней нормы доходности, а на малых предприятиях — срока окупаемости инвестиций и срока окупаемости эксплуатируемого объекта.
8.3. Показатель рентабельности инвестиций,
область его применения и методика расчета
Кроме показателя чистого приведенного дохода для оценки эффективности проектного решения на предприятиях среднего бизнеса широко применяется показатель рентабельности инвестиций. Можно сказать, что оба показателя имеют одну и ту же природу и отражают одну и ту же суть, но только под разным углом зрения.
Экономический смысл показателя рентабельности инвестиций заключается в том, что он отражает долю чистого приведенного дохода, приходящуюся на единицу дисконтированных к началу жизненного цикла проекта инвестиционных вложений. Этот показатель рентабельности инвестиций рассчитывается по формуле
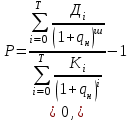(8.8).
В этой формуле все показатели и параметры имеют тот же экономический смысл, что и в формулах 8.6 и 8.7.
Если в данную формулу подставить исходную информацию рассмотренного в предыдущем параграфе примера, то при нормативе дисконтирования qн = 0,06 рентабельность инвестиций составит Р = 0,0804. Этот результат получается путем деления величины 5131,71 на величину 4749,99. Затем из частного от деления указанных величин вычитается единица и получается искомая рентабельность инвестиций — 0,0804.
Что же характеризует полученный результат, каков его экономический смысл? Он означает, что, применив данный вариант, инвестор полностью вернет свои инвестиционные вложения за жизненный цикл проекта и плюс к этому получит чистый дисконтированный доход в размере примерно 8% от авансированной суммы платежей.
Отмеченный результат расчета показан и на графике (рис. 8.1). Если двигаться по кривой влево и вверх до начала координат, то рентабельность инвестиций в этом случае составит Р = 0,8234. Это значит, что без учета фактора времени и упущенной выгоды, страховки и минимально установленной доходности проекта рентабельность инвестиций составит примерно 82,3%, т.е. затратив на проект 100 ден. единиц, инвестор после его окончания, получит полный доход 182,3 ден. единиц.
8.4. Показатели срока окупаемости инвестиций
и нового предпринимательского дела
∑ Дi = 0 + 0 + 0 + 502 + 520 + ... + 600 + 600 = 9252 тыс. руб.
Простое сравнение двух полученных величин свидетельствует о том, что доходная составляющая больше инвестиционной (9252 > 5074). Наличие именно такого неравенства однозначно определяет внутреннюю норму доходности как величину больше нуля.
Если бы две сравниваемые величины точно совпали, то тогда искомый показатель был бы равен нулю. И наконец, в случае когда инвестиционная сумма больше доходной составляющей, искомый показатель внутренней нормы доходности представляет отрицательную величину. Но тогда инвестор, очевидно, откажется от такого проекта и примет к рассмотрению исследуемый проект лишь тогда, когда доходы предприятия будут больше инвестиций. Именно такой случай рассматривается в нашем примере. Поэтому можно перейти к дальнейшему анализу и определению величины внутренней нормы доходности.
Второй шаг. Устанавливают величину искомого показателя на определенном уровне. Предположим, что расчетчик примет показатель q = 0,1, после чего произведет расчеты инвестиционных вложений и доходной составляющей проекта с применением принятой нормы доходности по формуле 8.2. Тогда у него получится отрицательная величина, ибо сумма инвестиций окажется больше доходной составляющей проекта (читатель может сам убедиться в этом, произведя соответствующие расчеты). Такой результат будет свидетельствовать о том, что установленная эмпирическим путем величина внутренней нормы доходности должна быть в данном проекте меньше 0,1 и, следовательно, дальнейший поиск связан с некоторым уменьшением величины этого показателя. Обычно если выполнять расчет чисто механически, то можно для дальнейших расчетов принять среднее значение показателя между двумя соседними расчетами, т.е. в нашем примере это будет q = 0,05, поскольку этот результат и есть средняя между 0 и 0,1.
Приняв новое значение внутренней нормы доходности, переходят к новому шагу в проводимых расчетах.
Третий шаг. Все расчеты точно повторяются, но уже с нормой доходности q= 0,05. Опять-таки возможны два случая: либо разность между доходной и инвестиционной частями проекта больше, либо она меньше нуля. Если имеет, место последний случай, то надо уменьшать внутреннюю норму доходности (например, до величины q
= 0,025) и все расчеты повторить. Если окажется, что разность двух составляющих проекта будет положительной, т.е. больше нуля (именно так случится в нашем примере, если все расчеты произвести по аналогии с ранее выполняемыми), то значение принимаемой нормы доходности надо будет вновь увеличить, доведя ее до величины q= 0,075. Это значение будет достаточно близким к истинной величине искомой нормы доходности, которая была получена на уровне q= 0,0698 с помощью компьютерной технологии.
Подобные расчеты можно продолжать многократно до получения искомого результата с такой точностью, какая будет нужна инвестору. В конечном счете потребность в информации о величине внутренней нормы доходности проекта встречается не так часто, чтобы на точности расчетов экономить несколько часов операционной работы.
В заключение следует отметить, что показатель внутренней нормы доходности применяется очень широко на многих предприятиях и многими инвесторами. Но особенно важное значение этот показатель имеет для крупных производств, для масштабных проектов, при реализации которых оцениваются их стратегичность и растянутость жизненного цикла, в течение которого проект будет приносить большой доход.
8.2. Показатель чистого приведенного дохода,
область его применения и методика расчета
Конкретная производственно-хозяйственная и предпринимательская практика чрезвычайно разнообразны как по масштабам будущего нового дела, так и по характеру используемой технологии, планируемой организации производства, проектируемой системы управления. Кроме того, проекты могут существенно различаться по длительности жизненного цикла, по срокам инвестиционных платежей, величине и характеру поступления во времени доходов функционирующего бизнеса и т.п.
Поэтому, чтобы иметь возможность отразить все имеющееся разнообразие форм и результатов предпринимательского бизнеса при оценке его эффективности, необходимо иметь несколько показателей. Одним из таких показателей является показатель чистого приведенного дохода (в экономической литературе его называют также чистой приведенной стоимостью).
Показатель чистого приведенного дохода довольно широко применяется в экономике. При его исчислении нормативная величина дохода рассматривается как упущенная выгода и поэтому считается как бы дополнительно понесенными затратами. Все, что получено предпринимателем сверх общих затрат (основных и дополнительных) отражает чистый приведенный доход.
Чистый приведенный доход рассчитывается по формуле
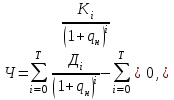(8.6)где Ч — чистый приведенный доход за жизненный цикл проекта;
Дi _ величина дохода в i -ом временном интервале (формула 8.3);
Кi _ величина инвестиционных платежей в i -ом временном интервале (формула 8.4);
Т — количество временных интервалов в жизненном цикле проекта (длительность временного интервала заранее устанавливается, например месяц, два месяца, и т.д.);
qн — норматив дисконтирования затрат и результатов проекта на момент начала его жизненного цикла
qн = qг+ qс + qо, (8.7)
где qг ― гарантированная норма получения дивидендов на вложенный капитал в высоконадежном банке (в долях единицы);
qс — страховая норма, учитывающая риск вложений (в долях единицы), наличие и полноту страхования инвестиционной деятельности (если предприниматель вообще не страхует свою деятельность, то страховая норма принимается по максимуму; если страховка имеется, то страховая норма уменьшается в зависимости от полноты страхования вплоть до нуля);
qо — минимальная граница доходности проекта (в долях единицы), которая по мнению предпринимателя может его устроить и принимается им для себя самостоятельно.
Рассчитаем на конкретном примере чистый приведенный доход по исходным данным, представленным в табл. 8.1. Дополнительно примем норматив дисконтирования q = 0,06. Его величина складывается из следующих элементов: qг= 0,035; qc= 0,01; qо = 0,015.
Тогда после подстановки исходных данных в формулу 8.6 получим
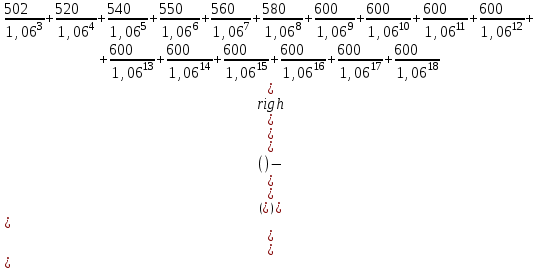
Таким образом, чистый приведенный доход составляет Ч = 381,72.
Как истолковать полученный результат? Прежде всего отметим, что на величину 381,72 денежных единиц проектируемый приведенный доход предприятия за жизненный цикл проекта превысит понесенные инвестором вложения. Это значит, что будущий доход предприятия полностью возместит осуществленные инвестиции и дополнительно обеспечит ему чистый доход в указанном размере. При этом в полученную сумму дохода не включаются упущенная выгода и страховка. Не учитывается в ней и заранее установленное ограничение в минимальном доходе. Все указанные элементы дохода также будут получены предприятием, но они гарантированы включенными в расчет нормативами. Поэтому подлинный доход предприятия будет значительно выше полученной расчетной суммы. Такова природа рассматриваемого показателя, который поэтому и называется чистым приведенным доходом. В нем подлинный доход от реализации проекта не показан, но, безусловно, подразумевается при оценке эффективности инвестиций и учитывается с помощью других показателей (например, при исчислении внутренней нормы доходности).
Проиллюстрируем экономический смысл показателя чистого приведенного дохода с помощью графика (рис. 8.1).
Вспомним, что в рассматриваемом примере показатель внутренней нормы доходности составляет q= 0,0698. Если норматив дисконтирования при расчете будет принят на уровне внутренней нормы доходности, т.е. равным 0,0698, то чистый приведенный доход в этом случае будет равен нулю. Это значит, что сверх установленного норматива предприятие никакого дохода не получит.
Теперь обратим внимание на горизонтальную линию с нулевым чистым приведенным доходом. Если норматив дисконтирования будет больше величины 0,0698, то чистый приведенный доход окажется величиной отрицательной и попадет на рассматриваемом графике в затемненную зону (например, при нормативе qн = 0,08).
Иная ситуация сложится, если норматив дисконтирования будет меньше величины внутренней нормы доходности (< 0,0698), т.е., как принято в рассматриваемом примере, q= 0,06. Тогда чистый приведенный доход будет больше нуля и составит величину Ч = 381,72.
Двигаясь влево к нулевой координате норматива дисконтирования, и тем самым снижая его величину, получим более высокий приведенный чистый доход, ибо движение к нулевому нормативу одновременно будет сопровождаться движением вверх по изображенной на графике кривой. При нулевой координате норматива дисконтирования чистый приведенный доход составит Ч = 4178 (разность между доходной составляющей проекта и величиной инвестиционных вложений без учета фактора времени, т.е. при qн = 0). По ранее произведенным расчетам (§ 8.1) эта разность получится, если (9252 5074) = 4178.
Рис.8.1. Определение чистого приведенного дохода и рентабельности инвестицийТаким образом, величина чистого приведенного дохода в огромной степени определяется не только объективными параметрами дохода предприятия и инвестициями в проект за его жизненный цикл, но и установленным нормативом дисконтирования. Если принятая норма окажется ошибочной, то будет иметь погрешность и величина чистого приведенного дохода. Поэтому при определении указанного норматива нужен тщательный анализ всей необходимой информации.
Рассматриваемый показатель достаточно широко распространен на предприятиях среднего бизнеса, реже он используется на предприятиях крупного и малого бизнеса, поскольку там главное внимание уделяется другим показателям. В частности, на крупных предприятиях предпочтение отдается показателю внутренней нормы доходности, а на малых предприятиях — срока окупаемости инвестиций и срока окупаемости эксплуатируемого объекта.
8.3. Показатель рентабельности инвестиций,
область его применения и методика расчета
Кроме показателя чистого приведенного дохода для оценки эффективности проектного решения на предприятиях среднего бизнеса широко применяется показатель рентабельности инвестиций. Можно сказать, что оба показателя имеют одну и ту же природу и отражают одну и ту же суть, но только под разным углом зрения.
Экономический смысл показателя рентабельности инвестиций заключается в том, что он отражает долю чистого приведенного дохода, приходящуюся на единицу дисконтированных к началу жизненного цикла проекта инвестиционных вложений. Этот показатель рентабельности инвестиций рассчитывается по формуле
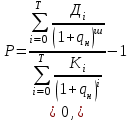(8.8).В этой формуле все показатели и параметры имеют тот же экономический смысл, что и в формулах 8.6 и 8.7.
Если в данную формулу подставить исходную информацию рассмотренного в предыдущем параграфе примера, то при нормативе дисконтирования qн = 0,06 рентабельность инвестиций составит Р = 0,0804. Этот результат получается путем деления величины 5131,71 на величину 4749,99. Затем из частного от деления указанных величин вычитается единица и получается искомая рентабельность инвестиций — 0,0804.
Что же характеризует полученный результат, каков его экономический смысл? Он означает, что, применив данный вариант, инвестор полностью вернет свои инвестиционные вложения за жизненный цикл проекта и плюс к этому получит чистый дисконтированный доход в размере примерно 8% от авансированной суммы платежей.
Отмеченный результат расчета показан и на графике (рис. 8.1). Если двигаться по кривой влево и вверх до начала координат, то рентабельность инвестиций в этом случае составит Р = 0,8234. Это значит, что без учета фактора времени и упущенной выгоды, страховки и минимально установленной доходности проекта рентабельность инвестиций составит примерно 82,3%, т.е. затратив на проект 100 ден. единиц, инвестор после его окончания, получит полный доход 182,3 ден. единиц.
8.4. Показатели срока окупаемости инвестиций
и нового предпринимательского дела