ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.03.2024
Просмотров: 65
Скачиваний: 0
СОДЕРЖАНИЕ
2) Оптимизация решений в условиях неопределенности
2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
3) Оценка операции по нескольким показателям.
4) Геометрическая интерпретация озлп.
Анализ положения l относительно одр.
Дадим геометрическую интерпретацию поиска оптимального решения.
Тогда (x1*, x2*, …, xn*) – оптимальное решение
5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
6) Симплекс-метод решения задачи лп.
7) Табличный алгоритм замены переменных.
8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.
13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
15. Решение игры в смешанных стратегиях.
Св. член равен -1 – это плохо!
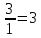 ;
- это для строки y1.
;
- это для строки y1.
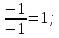 -
это для строки y2.
-
это для строки y2.
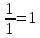 ;
- это для строки y4.
;
- это для строки y4.
Минимум для строк y2, y4 (можно выбрать любой).
Производим замену y2 x3, получаем
|
|
Св. член
|
y3
|
x2
|
y2
|
|
y1
|
2 |
3 |
2 |
1 |
|
x3
|
1 |
-2 |
-3 |
-1 |
|
x1 |
2 |
1 |
1 |
0
|
|
y4
|
0 |
2 |
2 |
1 |
Оптимальное решение найдено.
y3 x2 y2 0; y1 2; x3 1; x1 2; y4 0.
9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
|
*общее предисловие к вопросам 8 и 9 В задаче линейного программирования (ЛП) кроме уравнений-ограничений существует ещё и линейная функция L c0 c1x1 ... cjxj ... cnxn, => нужно минимизировать. После замены xj yi её нужно выразить через новые свободные переменные x1, x2,..., xj1, yi , xj1,..., xn. Для этого можно использовать тот же алгоритм, что и для преобразования любой строки таблицы. Действительно, т.к. L c0 (1x1 ... jxj ... nxn ) , где 1 c1; 2 c2; ... n cn, мы получим её одну строку (добавочную) стандартной таблицы, в которой никогда не выбирается разрешающий элемент. С помощью табличного алгоритма обмена переменных в уравнениях основной задачи ЛП (ОЗЛП) можно решить любую задачу ЛП. Нахождение решения распадается на 2 этапа=> т.е. на 8 и 9 вопрос (отыскание опорного решения и отыскание оптимального решения). |
Отыскание оптимального решения, минимизирующего линейную функцию L – т.е. попутно выясняется, ограничена ли снизу минимизируемая функция L.
Надо найти такое опорное решение, которое обращает в минимум линейную функцию
L c0 (1x1 ... jxj ... nxn ).
Принципиальную сторону вопроса мы уже рассматривали (как я поняла это то, что в табличке выше, но это не точно, мб сюда что-то из 2 вопроса). Здесь мы на примере покажем, как эта оптимизация м. б. проведена с помощью табличного алгоритма замены xj yi .
Сформулируем правила нахождения оптимального решения симплекс-методом.
1) Если все свободные члены (не считая строки L) в симплекс таблице неотрицательны, а в строке L (не считая свободного члена) нет ни одного
положительного элемента, то оптимальное решение достигнуто.
2) Если в строке L есть положительный элемент, а в столбце, соответствующем ему,
нет ни одного положительного элемента, то линейная функция L не ограничена
снизу и оптимального решения не существует.
3) Если в этом столбце есть положительные элементы, то следует произвести замену одной из свободных переменных на одну из базисных, причём в качестве разрешающего надо взять тот элемент этого столбца, для которого отношение к
нему соответствующего свободного члена минимально.
Пример
Найти решение задачи ЛП с уравнениями
y1 2 (x1 x2 2x3);
y2 1 (x1 x2 x3);
y3 5 (x2 x3);
y4 2 (2x1 x2);
обращающее в минимум линейную функцию L 0 (x1 2x2 x3).
Решение
Т.к. все свободные члены неотрицательны, то опорное решение налицо:
x1 x2 x3 0; y1 y4 2; y2 1; y3 5; L 0
Это решение не оптимально, т.к. коэффициент при x2 и x3 положительны (у линейной функции). Выберем x3, его надо поменять.
|
|
Св. член
|
x1
|
x2
|
x3, x3 y2
|
|
L
|
0 -1 |
-1 -1 |
2 1 |
1 -1 |
|
y1
|
2 2 |
1 2 |
1 -2 |
-2 2 |
|
y2 , y2 x3
|
1 1 |
1 1 |
-1 -1 |
1 λ=1 |
|
Y3 |
5 -1 |
0 -1 |
1 1 |
1 -1 |
|
y4
|
2 0 |
2 0 |
-1 0 |
0 0 |
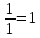 ;
- это для строки y2.
;
- это для строки y2.
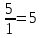 ;
- это для строки y3.
;
- это для строки y3.
По min выбираем y2.
|
|
Св. член
|
x1
|
x2, x2 y3
|
y2
|
|
L
|
-1 -6 |
-2 3/2 |
3 -3/2 |
-1 3/2 |
|
y1
|
4 2 |
3 -1/2 |
-1 1/2 |
2 -1/2 |
|
x3
|
1 2 |
1 -1/2 |
-1 1/2 |
1 -1/2 |
|
y3, y3 x2
|
4 2 |
-1 -1/2 |
2 λ=1/2 |
-1 -1/2 |
|
y4
|
2 2 |
2 -1/2 |
-1 1/2 |
0 -1/2 |
|
|
Св. член
|
x1
|
y3
|
y2, y2 y1
|
|
L
|
-7 -2 |
-1/2 -5/6 |
-3/2 -1/6 |
1/2 -1/3 |
|
y1 , y1 y2
|
6 4 |
5/2 5/3 |
1/2 1/3 |
3/2 λ=2/3 |
|
x3
|
3 -2 |
1/2 -5/6 |
1/2 -1/6 |
1/2 -1/3 |
|
x2
|
2 2 |
-1/2 5/6 |
1/2 1/6 |
-1/2 1/3 |
|
y4
|
4 2 |
3/2 5/6 |
1/2 1/6 |
-1/2 1/3 |
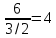 ;
- это для строки y1.
;
- это для строки y1.
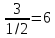 ;
- это для строки x3.
;
- это для строки x3.
По min выбираем y1.
|
|
Св. член
|
x1
|
y3
|
y1
|
|
L
|
-9 |
-8/6=-4/3 |
-10/6=-5/3 |
-1/3 |
|
y2
|
4 |
5/3 |
1/3 |
2/3 |
|
x3
|
1
|
-2/6=-1/3 |
2/6=1/3
|
-1/3 |
|
x2 |
4 |
1/3 |
4/6=2/3
|
1/3 |
|
y4
|
6
|
14/6=7/3 |
2/3
|
1/3 |
Т.к. в строке L нет ни одного положительного элемента, то оптимальное решение достигнуто.
x1 y3 y1 0; y2 x2 4; x3 1; y4 6; L 9.

