Файл: 1. Общественное здоровье и здравоохранение, экономика здравоохранения как интегративная наука. Основные разделы, задачи, значение в системе подготовки врача..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 169
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
23. Средний уровень признака. Средние величины: виды, свойства, практическое применение. Среднее квардратическое отклонение. Оценка достоверности результатов исследования.
Важным групповым свойством статистической совокупности является средний уровень признака, который характеризуется средними величинами (М).
1.Средняя величина - это величина, одним числом характеризующая всю совокупность в целом.
Виды:
средняя арифметическая,
средняя геометрическая,
средняя гармоническая,
средняя квадратическая,
средняя прогрессивная,
средняя хронологическая



В практической деятельности врача наиболее часто используются средняя арифметическая (М) и особые средние - мода (Мо) и медиана (Ме)
Практическое применение: применение в научных экспериментальных и клинических исследованиях
-для характеристики физиологических показателей организма в норме и патологии, при обработке лабораторных данных.
2. Среднее квардратическое отклонение.


3.Оценка достоверности результатов исследования.
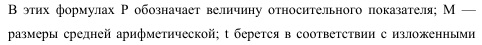
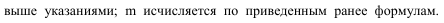



24. Разнообразие признака в статистической совокупности: критерии, характеризующие границы и внутреннюю структуру вариационного ряда, их практическое применение
Вариационный ряд – ряд числовых значений какого-то определенного признака, отличающихся друг от друга по всей величине и расположенных в ранговом порядке.
Используют для вычисления среднеквадратичного отклонения, степени вариации, получение средней величины, средней ошибки средней величины – параметры вариационного ряда.
Виды вариационного ряда:
Варианта – числовое значение изучаемого признака (каждое число) (V).
Частота (Р) – с которой встречается каждая варианта.
• число наблюдений (n) - сумма всех частот ( n = ∑ P)
• интервал - разность между двумя соседними вариантами (V3-V2 , V2-V1, т.д.)
• амплитуда - разность между наибольшей и наименьшей вариантами (Vmax - Vmin)
Мода(Mo) – наиболее часто встречающаяся варианта в вариационном ряду.
Медиана(Me) – варианта, делящая вариационный ряд на 2 равные части.
Если число наблюдений четное, то место расположения середины вариационного ряда определяется по формуле n/2 , если нечетное - n + 1/ 2
25. Методы изучения связи между явлениями и признаками, практическое применение. Оценка силы и характера корреляционной связи. Парная и множественная корреляция.
При изучения общественного здоровья и здравоохранения часто проводят параллели между факторными и результативными явлениями (причинно – следственные связи) или зависимость двух параллельных признаков от третьей величины. Для этого необходимо знать направление этой связи, ее достоверность, сила связи, ее размер. Для этого используют методы корреляции. 2 вида:
Функциональная – такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого. Характерно для физико – химических процессов (площадь круга от радиуса круга).
Корреляционная – такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между массой и ростом). Характерна для социально – гигиенических процессов, клинической медициной, биологией.
Практическое значение корреляционной связи:
1. выявление причинно – следственной связи между факторными и результативными признаками.
2. зависимость двух параллельных признаков от третьей величины (от повышения температуры – изменение давления, пульса).
3. позволяет изучить взаимодействие факторов, измерить силу, характер и направленность влияния одних факторов на другие.
Коэффициент корреляции – величина, характеризующая направление и силу связи между признаками. Представлен таблицей, график (диаграмма рассеяния), коэффициент корреляции.
Число наблюдений не менее 30.
В статистике принято различать следующие варианты зависимостей:
Парная корреляция – связь между признаками (результативным и факторным признаками или двумя факторными).
Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
26. Стандартизированные показатели. Этапы прямого метода стандартизации. Практическое использование.
Стандартизация – метод расчета условных (стандартизированных) показателей, замещающих интенсивные показатели в тех случаях, когда сравнение последних недопустимо из-за несоответствия сравниваемых групп.
Стандартизированные показатели – это условные, гипотетические величины, они не отражают истинных размеров явлений. Стандартизированные показатели свидетельствуют о том, каковы были бы значения сравниваемых интенсивных показателей, если бы были исключены различия в составах совокупностей.
Таким образом, метод стандартизации применяется для выявления влияния фактора неоднородности составов совокупностей по какому-либо признаку на величину сравниваемых интенсивных показателей
Прямой метод – наличие полных сведений как о составе сравниваемых совокупностей, так и распределении в них явлений.
Этапы расчета стандартизированных показателей:
1 этап. Расчет общих и частных интенсивных показателей.
Общих – совокупностям в целом, частных – по признаку различия (пол, возраст, стаж работы).
2 этап. Определение стандарта, т.е. выбор одинакового численного состава среды по данному признаку (возраст, пол) для сравниваемых совокупностей. Стандартом может стать состав любой совокупности из сравниваемых совокупностей или любой другой аналогичный состав совокупности. Уравниваются условия среды, «ожидаемые величины».
3 этап. Вычисление ожидаемых абсолютных величин в группах стандартов на основе групповых интенсивных показателей, рассчитанных на 1 этапе. Итоговые числа – сумма ожидаемых величин в группах.
4 этап. Вычисление стандартизированных показателей для сравниваемых совокупностей.
5 этап. Сопоставление стандартизированных и интенсивных показателей, формулировка выводов.
Практическое использование – применяется при сравнении интенсивных показателей в совокупностях, отличающихся по составу (например, по возрасту, полу, профессиям и т.д.)
27.Здоровье населения. Определение. Современные представления о здоровье как важнейшей характеристике уровня жизни. Факторы, влияющие на здоровье населения, функции здоровья.
Здоровье населения – характеристика состояния здоровья членов социальной общности, измеряемая комплексом социально-демографических показателей:
Здоровье – взаимосвязь с социальной ситуацией через факторы успешной или неуспешной адаптации (от индивидуальных биофизических или психологических характеристик до социокультурной реальности). Все болезни по существу социальны.
К. Маркса: «болезнь это стесненная в своей свободе жизнь». Речь о свободе, обеспечиваемой социальным благополучием человека.
Осуществление основных функций здоровья, к которым относят живой труд, воспроизводство и развитие личности невозможно вне социального бытия человека. Эти представления легли в основу «социальной концепции здоровья»
Критерии индивидуального здоровья
Важным групповым свойством статистической совокупности является средний уровень признака, который характеризуется средними величинами (М).
1.Средняя величина - это величина, одним числом характеризующая всю совокупность в целом.
Виды:
средняя арифметическая,
средняя геометрическая,
средняя гармоническая,
средняя квадратическая,
средняя прогрессивная,
средняя хронологическая



В практической деятельности врача наиболее часто используются средняя арифметическая (М) и особые средние - мода (Мо) и медиана (Ме)
Практическое применение: применение в научных экспериментальных и клинических исследованиях
-для характеристики физиологических показателей организма в норме и патологии, при обработке лабораторных данных.
-
для оценки здоровья населения, при характеристике физического развития (средний рост, средняя масса тела), -
-при анализе деятельности лечебно-профилактических учреждений (показатели нагрузки врачей, посещаемости поликлиники, среднее число жителей на участке, среднегодовая занятость больничной койки, средняя длительность пребывания в стационаре и пр.). -
-в социально- гигиенических исследованиях: средняя жилая площадь на человека, средний возраст, средний стаж работы в группах работающих, среднее содержание химиче- ского вещества во внешней среде и т.д.
2. Среднее квардратическое отклонение.


3.Оценка достоверности результатов исследования.




24. Разнообразие признака в статистической совокупности: критерии, характеризующие границы и внутреннюю структуру вариационного ряда, их практическое применение
Вариационный ряд – ряд числовых значений какого-то определенного признака, отличающихся друг от друга по всей величине и расположенных в ранговом порядке.
Используют для вычисления среднеквадратичного отклонения, степени вариации, получение средней величины, средней ошибки средней величины – параметры вариационного ряда.
Виды вариационного ряда:
-
ранжированный (упорядоченный) ряд - такой, в котором числовые значения вариант располагаются последовательно, по убыванию или по нарастанию (5, 7, 8, 12, 26, 31, 38 и т.д.) неранжированный ряд - такой, в котором варианты располагаются беспорядочно (34, 6, 12, 45, 24, 7, 98 и т. д.) -
прерывный (дискретный) ряд - такой, в котором варианты выражены только целым числом и не могут иметь промежуточных значений (число детей в семье, число лейкоцитов в крови, частота пульса, число посещений, пр.) -
непрерывный ряд - такой, в котором варианты могут принимать любые значения, в том числе и дробные (рост, масса тела, время, затраченное на прием одного больного, содержание в крови или воздухе различных веществ, пр.) -
простой (развернутый) ряд - такой, в котором каждая варианта и соответствующая ей частота обозначены отдельно. Ряд, в котором каждая варианта встречается с частотой, равной единице, называется простым невзвешенным, а если с разной частотой - простым взвешенным. -
сгруппированный (интервальный) ряд - такой, в котором варианты соединены в группы, объединяющие их по величине в пределах определенного интервала. -
Четкий/нечеткий
Варианта – числовое значение изучаемого признака (каждое число) (V).
Частота (Р) – с которой встречается каждая варианта.
• число наблюдений (n) - сумма всех частот ( n = ∑ P)
• интервал - разность между двумя соседними вариантами (V3-V2 , V2-V1, т.д.)
• амплитуда - разность между наибольшей и наименьшей вариантами (Vmax - Vmin)
Мода(Mo) – наиболее часто встречающаяся варианта в вариационном ряду.
Медиана(Me) – варианта, делящая вариационный ряд на 2 равные части.
Если число наблюдений четное, то место расположения середины вариационного ряда определяется по формуле n/2 , если нечетное - n + 1/ 2
25. Методы изучения связи между явлениями и признаками, практическое применение. Оценка силы и характера корреляционной связи. Парная и множественная корреляция.
При изучения общественного здоровья и здравоохранения часто проводят параллели между факторными и результативными явлениями (причинно – следственные связи) или зависимость двух параллельных признаков от третьей величины. Для этого необходимо знать направление этой связи, ее достоверность, сила связи, ее размер. Для этого используют методы корреляции. 2 вида:
Функциональная – такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого. Характерно для физико – химических процессов (площадь круга от радиуса круга).
Корреляционная – такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между массой и ростом). Характерна для социально – гигиенических процессов, клинической медициной, биологией.
Практическое значение корреляционной связи:
1. выявление причинно – следственной связи между факторными и результативными признаками.
2. зависимость двух параллельных признаков от третьей величины (от повышения температуры – изменение давления, пульса).
3. позволяет изучить взаимодействие факторов, измерить силу, характер и направленность влияния одних факторов на другие.
Коэффициент корреляции – величина, характеризующая направление и силу связи между признаками. Представлен таблицей, график (диаграмма рассеяния), коэффициент корреляции.
Число наблюдений не менее 30.
| Сила связи | | Характер связи | | |||||
| | Прямая + | Обратная - | | |||||
| Полная | 1 | | 1 | | ||||
| Сильная | 0,7 - 0,9 | | 0,7 - 0,9 | |||||
| Средняя | 0,3 - 0,6 | | 0,3 - 0,6 | |||||
| Слабая | 0 - 0,2 | | 0 - 0,2 | |||||
| Отсутствует | 0 | | 0 | |||||
В статистике принято различать следующие варианты зависимостей:
Парная корреляция – связь между признаками (результативным и факторным признаками или двумя факторными).
Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
26. Стандартизированные показатели. Этапы прямого метода стандартизации. Практическое использование.
Стандартизация – метод расчета условных (стандартизированных) показателей, замещающих интенсивные показатели в тех случаях, когда сравнение последних недопустимо из-за несоответствия сравниваемых групп.
Стандартизированные показатели – это условные, гипотетические величины, они не отражают истинных размеров явлений. Стандартизированные показатели свидетельствуют о том, каковы были бы значения сравниваемых интенсивных показателей, если бы были исключены различия в составах совокупностей.
Таким образом, метод стандартизации применяется для выявления влияния фактора неоднородности составов совокупностей по какому-либо признаку на величину сравниваемых интенсивных показателей
Прямой метод – наличие полных сведений как о составе сравниваемых совокупностей, так и распределении в них явлений.
Этапы расчета стандартизированных показателей:
1 этап. Расчет общих и частных интенсивных показателей.
Общих – совокупностям в целом, частных – по признаку различия (пол, возраст, стаж работы).
2 этап. Определение стандарта, т.е. выбор одинакового численного состава среды по данному признаку (возраст, пол) для сравниваемых совокупностей. Стандартом может стать состав любой совокупности из сравниваемых совокупностей или любой другой аналогичный состав совокупности. Уравниваются условия среды, «ожидаемые величины».
3 этап. Вычисление ожидаемых абсолютных величин в группах стандартов на основе групповых интенсивных показателей, рассчитанных на 1 этапе. Итоговые числа – сумма ожидаемых величин в группах.
4 этап. Вычисление стандартизированных показателей для сравниваемых совокупностей.
5 этап. Сопоставление стандартизированных и интенсивных показателей, формулировка выводов.
Практическое использование – применяется при сравнении интенсивных показателей в совокупностях, отличающихся по составу (например, по возрасту, полу, профессиям и т.д.)
27.Здоровье населения. Определение. Современные представления о здоровье как важнейшей характеристике уровня жизни. Факторы, влияющие на здоровье населения, функции здоровья.
Здоровье населения – характеристика состояния здоровья членов социальной общности, измеряемая комплексом социально-демографических показателей:
-
рождаемостью, -
смертностью, -
средней продолжительностью жизни, -
заболеваемостью, -
уровнем физического развития.
Здоровье – взаимосвязь с социальной ситуацией через факторы успешной или неуспешной адаптации (от индивидуальных биофизических или психологических характеристик до социокультурной реальности). Все болезни по существу социальны.
К. Маркса: «болезнь это стесненная в своей свободе жизнь». Речь о свободе, обеспечиваемой социальным благополучием человека.
Осуществление основных функций здоровья, к которым относят живой труд, воспроизводство и развитие личности невозможно вне социального бытия человека. Эти представления легли в основу «социальной концепции здоровья»
Критерии индивидуального здоровья
| Субъективные | Объективные |
|
|

