Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 377
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
а)
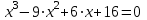 ; б)
; б) 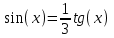
Решение. Рассмотрим по шагам решение уравнения из пункта а).
1) вводим уравнение:
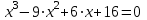 . Чтобы MathCad не принял вводимый знак «=» за запрос ответа для введенного выражения, знак равенства нужно вводить двумя клавишами [Ctrl]+[=];
. Чтобы MathCad не принял вводимый знак «=» за запрос ответа для введенного выражения, знак равенства нужно вводить двумя клавишами [Ctrl]+[=];2) щелчком мыши выделяем в уравнении переменную, относительно которой это уравнение нужно решить. В нашем случае это x;
3) вызываем пункт Variable | Solve из меню Symbolics.
После выполнения этих трех действий MathCad выведет на экран в виде столбца решение нашего уравнения. В нашем случае это будет столбец из трех чисел: -1, 2, 8.
Аналогичным образом поступаем с пунктом б) примера. Получаем столбец:
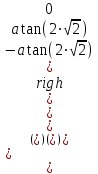 .
.Задание 2. Найти решения следующих уравнений:
а)
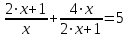 ; б)
; б) 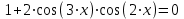 .
.Этим же способом можно решать не только числовые уравнения, но и уравнения с переменными коэффициентами, частным случаем которых являются уравнения с параметрами. Рассмотрим, как это делается.
Пример. Решить следующее уравнение:
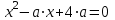 .
.Решение (аналогично способу 2):
1) вводим уравнение, используя комбинацию клавиш [Ctrl]+[=] вместо клавиши «=»:
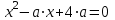 ;
;2) щелчком мыши выделяем переменную x для поиска ее значений;
3) вызываем пункт Variable | Solve меню Symbolics;
4) смотрим ответ:
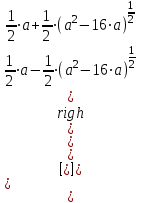 .
.Таким же образом можно решить это уравнение, но относительно переменной a, приняв x за параметр. Для этого необходимо щелчком мыши вместо переменной x во втором шаге выделить переменную a.
Получим ответ:
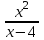 .
.Задание 1.
Разложить выражение на правильные дроби.
Пример
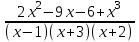
Набрать
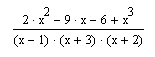
Выделит курсором переменную х и выполнить команду: Symboliecs/Variadle/Convert to Partial Fraction
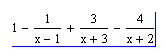
Варианты заданий
| 1. | 7. |
| 2. | 8. |
| 3. | 9. 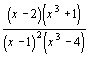 |
| 4. | 10. 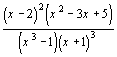 |
| 5. | 11. 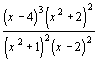 |
| 6. | 12. 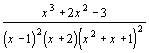 |
Задание 2.
1. Решение линейных и нелинейных уравнений.
Пример.
Решить уравнение
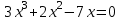
1. Способ. Чтобы решить уравнение символьно необходимо:
-
Напечатать выражение (не печатать знак равенства 0). -
Выделить переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью. -
Выбрать пункт меню Symbolics,Variable, Solve (Символы, Переменные, Вычислить).
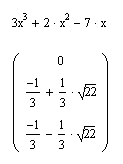
2. Способ.
Для решения с помощью вычислительного блока Given/Find необходимо:
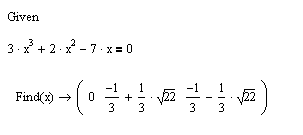
2. Построение вектора v, содержащего коэффициенты полинома
Набрать полином, выделить курсором переменную х и выполнить команду Symbolics, Polynomial Coefficient
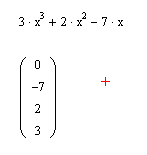
1. Решить уравнение двумя способами.
2. Построить вектор v, содержащий коэффициенты полинома.
| № варианта | g(x) | № варианта | g(x) |
| 1 | x4 - 2x3 + x2 - 12x + 20 | 9 | x4 + x3 - 17x2 - 45x - 100 |
| 2 | x4 + 6x3 + x2 - 4x - 60 | 10 | x4 - 5x3 + x2 - 15x + 50 |
| 3 | x4 - 14x2 - 40x - 75 | 11 | x4 - 4x3 - 2x2 - 20x + 25 |
| 4 | x4 - x3 + x2 - 11x + 10 | 12 | x4 + 5x3 + 7x2 + 7x - 20 |
| 5 | x4 - x3 - 29x2 - 71x -140 | 13 | x4 - 7x3 + 7x2 - 5x + 100 |
| 6 | x4 + 7x3 + 9x2 + 13x - 30 | 14 | x4 + 10x3 +36x2 +70x+ 75 |
| 7 | x4 + 3x3 - 23x2 - 55x - 150 | 15 | x4 + 9x3 + 31x2 + 59x+ 60 |
| 8 | x4 - 6x3 + 4x2 + 10x + 75 | 16 | x4 + 19x3 + 21x2 + 39x+ 40 |
Задание 3.
Решить уравнение с помощью функции root
F(x)=cosx+0,2 на интервале [0..2]
Решение
Способ 1
-
Определить функцию F(x) -
Определить переменную х -
Определить точность вычислений Math, Options, Tolerance =0,0001 -
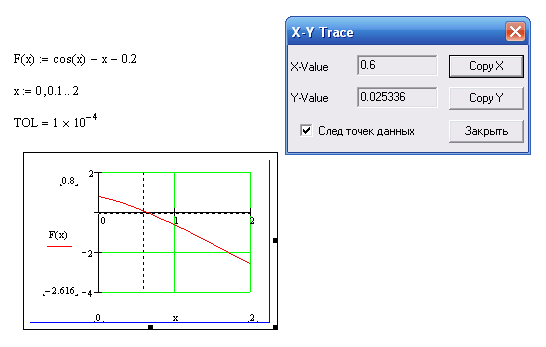
Построить график, с помощью команды Format вывести оси координат, вспомогательные линии. -
С помощью команды Trace на графике определить координаты точки пересечения графика с осью ОХ. х=0,6
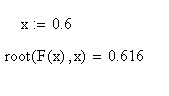
-
Записать
Способ 2.
Записать
Варианты заданий
| Номер варианта | Функция | Номер варианта | Функция |
| 1 | | 7 | |
| 2 | | 8 | |
| 3 | | 9 | |
| 4 | | 10 | |
| 5 | | 11 | |
| 6 | | 12 | |
Задание 4.
Найти корни уравнения, зависящего от двух переменных.
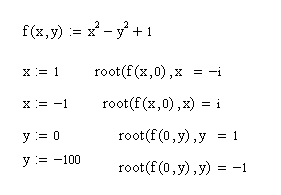
Задание 5.
Н
 айти корни полинома 0,75х3-8х+5
айти корни полинома 0,75х3-8х+5Решение.
-
Записать полином -
Выделить курсором переменную х и выполнить команду Symbolic, Polynomial Coefficients -
Определить вектор V, копировав значения полученных коэффициентов -
Записать функцию poyroots(v)
| Номер варианта | g(x) | Номер варианта | g(x) |
| 1 | 10x4 +22x3 + x2 - 16x - 20 | 9 | 25x4 + 13x3 - 17x2 - 45x - 10 |
| 2 | 11x4 -36x3 + x2 - 44x +26 | 10 | 26x4 - 15x3 + 11x2 - 15x + 140 |
| 3 | x4 - 14x2 + x - 15 | 11 | 23x4 - 42x3 - 2x2 + 25 |
| 4 | 18x4 + 15x3 + x2 - 11x + 10 | 12 | 27x4 + 65x3 + 47x2 + 7x - 20 |
| 5 | 25x4 +2 x3 - 9x2 - 71x -140 | 13 | x4 - 7x3 + 7x2 - 5x + 100 |
| 6 | 36x4 - 47x3 + 29x2 + 3x - 30 | 14 | x4 + 10x3 +36x2 +70x+ 75 |
| 7 | x4 + 13x3 - 43x2 + 75x - 1 | 15 | x4 + 9x3 + 31x2 + 59x+ 60 |
| 8 | 2x4 + 16x3 + 4x2 + 10x + 2 | 16 | x4 + 19x3 + 21x2 + 39x+ 40 |
Контрольные вопросы
-
Какие функции для решения одного уравнения в Mathcad вы знаете? В чем их отличие? -
Какие аргументы функции root не обязательны? -
В каких случаях Mathcad не может найти корень уравнения? -
Какая системная переменная отвечает за точность вычислений? -
Как изменить точность, с которой функция root ищет корень? -
Как системная переменная TOL влияет на решение уравнения с помощью функции root? -
Назовите функции для решения систем уравнений в Mathcad и особенности их применения. -
Опишите структуру блока решения уравнений. -
Какой знак равенства используется в блоке решения? Какой комбинацией клавиш вставляется в документ? -
Какие выражения не допустимы внутри блока решения уравнения? -
Опишите способы использования функции Find. -
В каких случаях Mathcad не может найти решение системы уравнений? -
Дайте сравнительную характеристику функциям Find и Minerr.
Практитческая работа 7.
Решение систем уравнений в MathCAD.
Цель работы: освоение решения систем уравнений в MathCAD.
Порядок выполнения работы:
-
Освоить методику решения систем уравнений в MathCAD. -
Выполнить задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы.
