Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 383
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
4. Найти обратные матрицы.
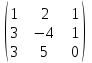 | 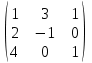 |  | 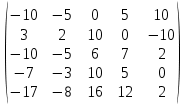 |
5. Решить системы линейных уравнений методом Крамера.
2
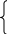
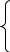
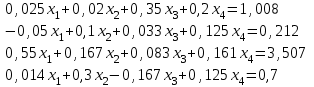 х1 - 4х2 + 4х3 = 10
х1 - 4х2 + 4х3 = 10 -3х1 + 8х2 - 10х3= -25
4х1 - 3х2 + х3 = 1
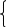 х1 + 2х2 – х3 = 7
х1 + 2х2 – х3 = 72х1 - х2 + х3 = 3
3х1 - 5х2 + 2х3= 0
Вариант №6
-
Вычислить определители
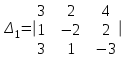

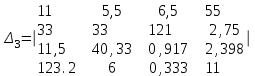
2. Найти произведение матриц АВ и ВА; CD и DC
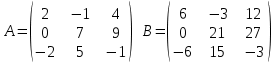
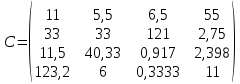
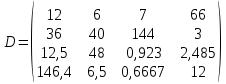
3. Найти транспонированные матрицы
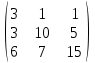 |  | 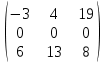 | 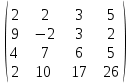 | 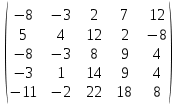 |
4. Найти обратные.
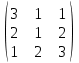 |  | 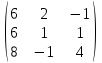 | 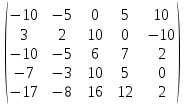 |
5. Решить системы линейных уравнений методом Крамера.


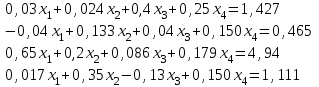
х1 + 2х2 – х3 = 7
2х1 - х2 + х3 = 3
3х1 - 5х2 + 2х3= 0

х1+ х2-2х3 +2х4= -2
3х1+2х2-2х3 + х4 = -6
7х1+4х2+2х3+3х4 = -6
2х1-2х2- х3 + х4 = 0
Вариант №7
-
Вычислить определители
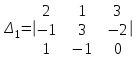
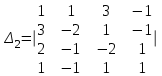
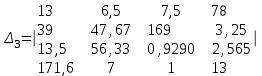
2. Найти произведение матриц АВ и ВА; CD и DC
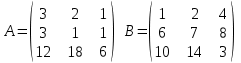
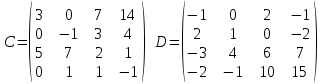
3. Найти транспонированные матрицы
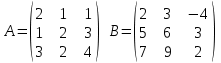
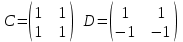
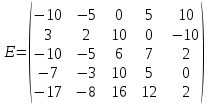
4. Найти обратные матрицы.
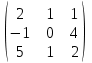 | 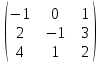 | 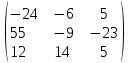 | 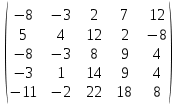 |
5 . Решить системы линейных уравнений методом Крамера.
. Решить системы линейных уравнений методом Крамера.
 х1+ х2-3х3= -1 2х1+2х2- 2х3 + 7х4= 0
х1+ х2-3х3= -1 2х1+2х2- 2х3 + 7х4= 02х1+ х2-2х3= 1 х1- х2+ х3 - 9х4= 2
х1+ х2+ х3= 3 -х1+ 2х2- х3+10х4= 0
х1+2х2-3х3= 1
Вариант №8
-
Вычислить определители
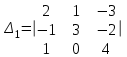
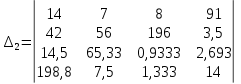
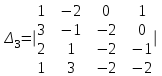
2. Найти произведение матриц АВ и ВА; CD и DC
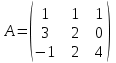 | 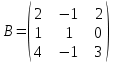 | 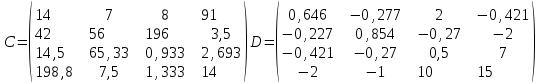 |
3. Найти транспонированные матрицы
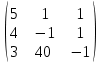 | 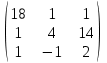 | 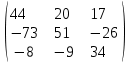 |  |
-
Найти обратные матрицы.
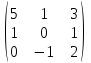 | 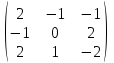 | 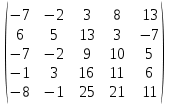 |  |
5. Решить системы линейных уравнений методом Крамера.
2
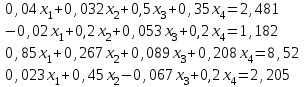 х1 + х2 – х3 = 5
х1 + х2 – х3 = 5 х1 + х2 + х3 = 2
х1 - х2 + 2х3= -3
4
 х1 + х2 – 3х3= -1
х1 + х2 – 3х3= -18х1 + 3х2 - 6х3= -1
х1 + х2 - х3= -1
Вариант №9
-
Вычислить определители
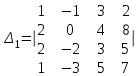
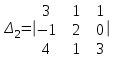
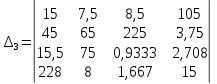
2. Найти произведение матриц АВ и ВА; CD и DC
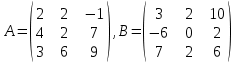
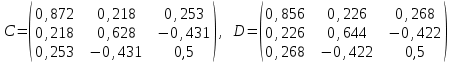
3. Найти транспонированные матрицы
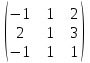 | 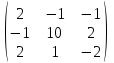 | 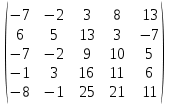 | 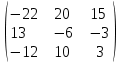 |
4. Найти обратные матрицы.
 | 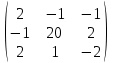 | 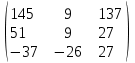 | 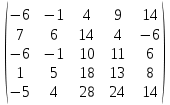 |
5. Решить системы линейных уравнений методом Крамера.

х
 1+ х2 + х3+ х4+ х5= 7 х1+2х2-4х3= 1
1+ х2 + х3+ х4+ х5= 7 х1+2х2-4х3= 13х1+2х2+ х3+ х4-3х5= -2 2х1+ х2-5х3= -1
х2+2х3+2х4+6х5=23 х1- х2- х3= -2
5х1+4х2+3х3+3х4- х5=12
-5х1+41х2+3х3+3х4- х5=172