Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 374
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
 (t)
(t) 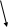
t
Если известны границы интервала аргумента, но неизвестен шаг, алгоритм следующий:
Построить график функции y=sin(x-20) на интервале [1,20]
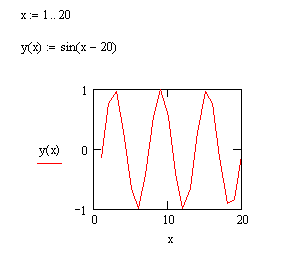
Если известны границы интервала аргумента, и задан шаг, алгоритм следующий:
Построить график функции
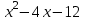 на интервале [1,15] с шагом 0,1
на интервале [1,15] с шагом 0,1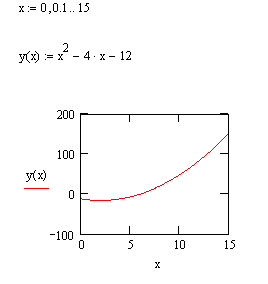
Варианты заданий
| Вариант | Функции | ||
| 1 | | 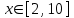 | 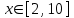 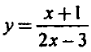 Шаг 0,2 |
| 2 | | 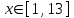 | 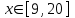 Шаг 0,2 |
| 3 | | 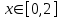 | 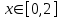 Шаг 0,3 |
| 4 | | 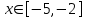 | 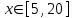 Шаг 0,1 |
| 5 | | 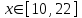 | 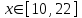 Шаг 0,5 Шаг 0,5 |
| 6 | | 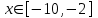 | 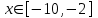 Шаг 0,5 |
| 7 | | 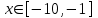 | 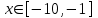 Шаг 0,25 |
| 8 | | 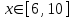 | 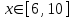 Шаг 0,55 Шаг 0,55 |
| 9 | | 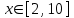 | 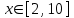 Шаг 0,15 |
| 10 | | 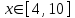 | 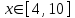 Шаг 0,12 Шаг 0,12 |
| 11 | | 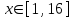 | 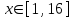 Шаг 0,22 Шаг 0,22 |
| 12 | | 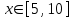 | 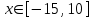 Шаг 0,5 Шаг 0,5 |
Задание 2.
Построить два графика в декартовых координатах X-Y следующих функций.
Пример
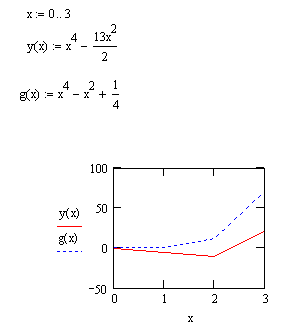 В шаблоне y(x) и g(x) набирать через запятую
В шаблоне y(x) и g(x) набирать через запятуюЗадание 3.
Решить графически уравнение
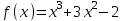 на интервале [0,10].
на интервале [0,10].-
Построить график
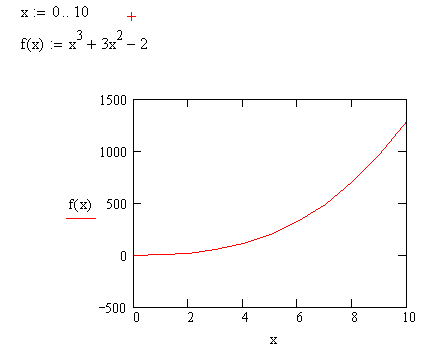
-
Для нахождения корней нужно найти точки пересечения графика с осью ОY, для этого выделит график, щелкнуть правой кнопкой мыши и выбрать Trace.
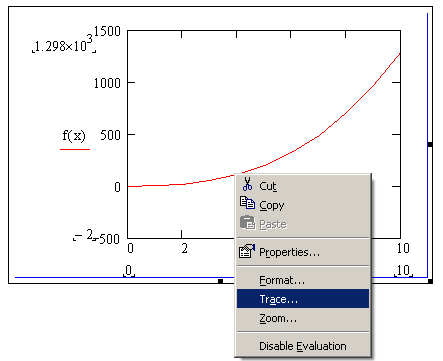
Навести указатель мыши на точку пересечения, после этого появятся координаты
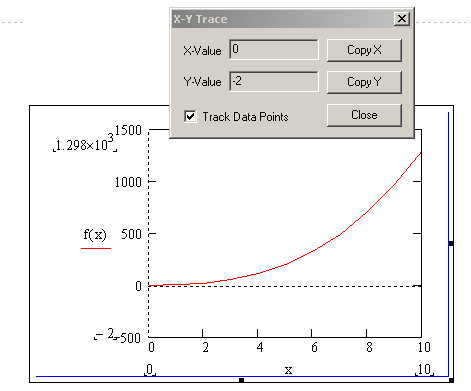
Контрольные вопросы
-
Как построить графики: поверхности; полярный; декартовый? -
Как построить несколько графиков в одной системе координат? -
Как изменить масштаб графика? -
Как определить координату точки на графике?
Практитческая работа 3.
Вычисление производных в MathCAD.
Цель работы: приобретение практических навыков вычисления производных в MathCAD.
Порядок выполнения работы:
-
Выполнить задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы
Общие сведения
Производные и их вычисление
Задание 1. Найти по определению производные следующих функций:
а)
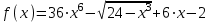 , при
, при 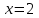 ;
;б)
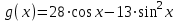 , при
, при 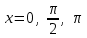 .
.Данный способ фактически требует от MathCad нахождения предела, а не производной. MathCad же имеет встроенные средства и для вычисления собственно производных.
В пакете MathCad, как обычно, имеется два способа вычисления производных функций. Первый способ - численный - дает возможность найти числовое значение производной в некоторой точке. Второй способ - символьный - дает возможность получить символьное значение производной функции. Рассмотрим оба эти способа.
Численный метод (производная в точке).
Пример. Найти значение производной функции
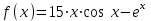 при x = 1; 0; 3,5.
при x = 1; 0; 3,5.Решение.
1) определим функцию
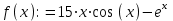 ;
;2) определим другую функцию, например g(x), равную производной функции f(x). Для этого щелкнем мышкой ниже определения функции f(x), введем начало определения функции и введем знак [?], появится оператор производной следующего вида:
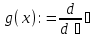
3) заполним соответствующие пустые поля. Щелкнем на нижнем поле и введем переменную x, по которой будем искать производную. В верхнем пустом поле введем имя функции f(x).
Получим следующее:
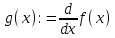
4) определив функцию g(x), используем ее. Найдем значения функции в заданных точках:
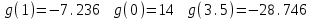 .
.Задание 2. Найти значения производных следующих Символьное вычисление производной (производная функции).
Для того чтобы найти производную функции в символьном виде, необходимо воспользоваться следующим способом.
Пример. Найти производные следующих функций:
а)
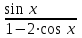
, б)
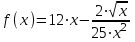 .
.Решение. Будем искать производную для случая а):
1) вызовем оператор производной, нажав клавишу «?», появится оператор производной следующего вида:
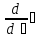 .
.2) заполним соответствующие пустые поля. Щелкнем в нижнем поле и введем переменную x, по которой будем искать производную. В верхнем пустом поле введем нашу функцию:
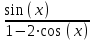 . Получим следующее:
. Получим следующее: 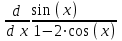 .
.3) нажмем комбинацию клавиш [Shift]+[F9].
MathCad выдаст следующее значение производной:
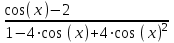
Аналогично поступаем с пунктом б) примера.
Получим ответ:
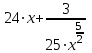 .
.Задание 1.
Найти производную от заданной функции и построить графики исходной функции и ее производной.
Пример.
У(х)=х2
-
Записываем выражение функции -
Выделить курсором переменную х и в главном меню выбрать Symboliecs/Variadle/Differentiate.
На экране появится:
-
Записать:
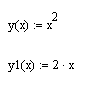
-
П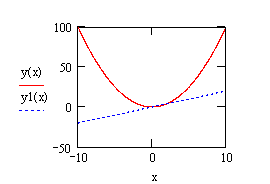 остроить графики: Кнопка . В шаблоне ввести в нижней части х, сбоку через запятую у(х), у1(х)
остроить графики: Кнопка . В шаблоне ввести в нижней части х, сбоку через запятую у(х), у1(х)
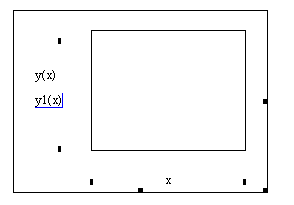
Щелкнуть в центр шаблона. Получим графики.
Варианты заданий.
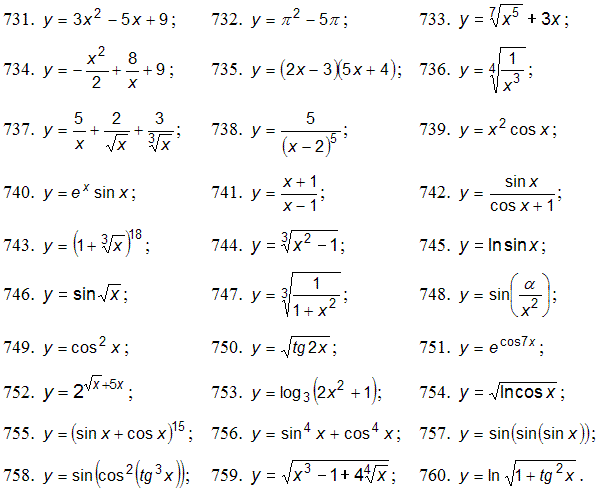
Задание 2.
Пример
Для функции у=х3 найти первую производную при х=2
-
Набрать -
Выбрать шаблон . В знаменателе ввести х в правую часть х3 , нажать =, получится результат .
Варианты заданий
1. Для функции F(x) = 3 x2 - 4x +9 найти F'(1).
2. Для функции F(x) = sin2x найти
3. Для функции найти
4. Для функции
найти F'(-1,5).
5. Для функции F(x) = x ln(x2 + 2x - 7) найти F'(2).
6. Для функции
7. Для функции F(x) = 5 ex - 8x найти F'(ln 3).
8. Для функции
9. Для функции
10. Для функции
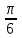 )
)Задание 3.
Пример
Найти производные второго порядка для функции
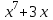
-
Набрать -
Выделить курсором переменную х и в главном меню выбрать Symboliecs/Variadle/Differentiate.
На экране появится:
-
Выделить курсором переменную х и в главном меню выбрать Symboliecs/Variadle/Differentiate.
На экране появится:
Варианты заданий
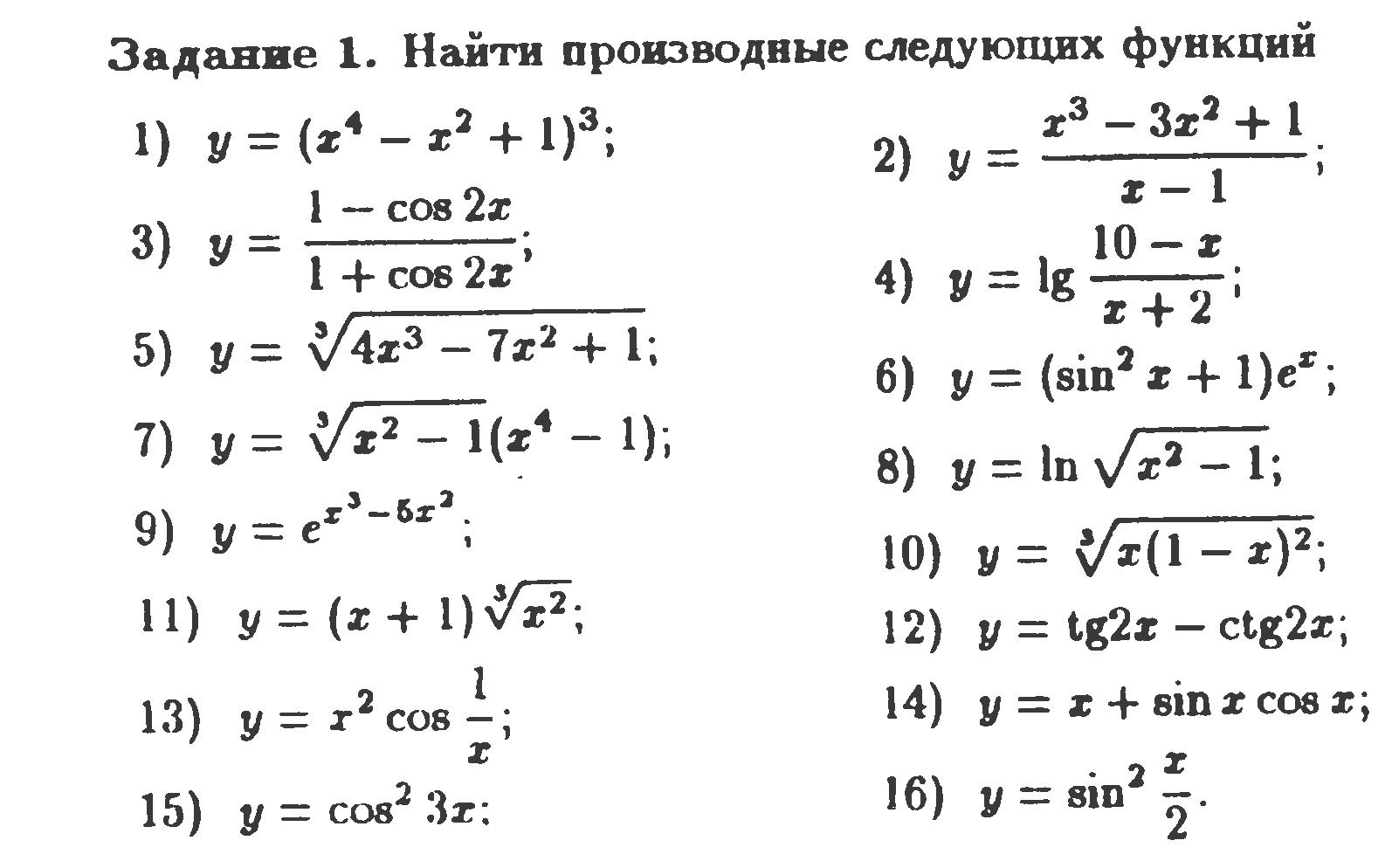
Задание 3.
Пример
Для функции у = cos8х найти вторую производную при х =
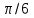
-
Набрать -
Выбрать шаблон . В знаменателе ввести х , в индекс 2, в правую часть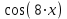
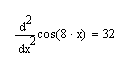 .
.В
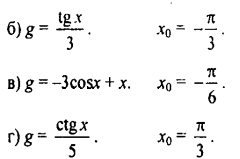 арианты заданий
арианты заданий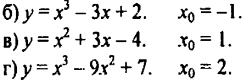
1
2
3
4
5
6
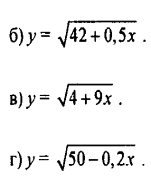
7
8
9
Х=10
Х=20
Х=100
