Файл: Методические рекомендации по проведению практических занятий по дисциплине ОП. 05. Информационные технологии.docx
Добавлен: 28.03.2024
Просмотров: 359
Скачиваний: 0
СОДЕРЖАНИЕ
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5 . Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5.Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
3. Найти транспонированные матрицы
5. Решить системы линейных уравнений методом Крамера.
Системы уравнений и их решение
Другие способы решения неравенств
Системы неравенств и их решение.
Задание 3
Выполнить вычисления с использованием стандартных функций и перевода градусов в радианы:
Пример:
Вычислить
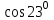
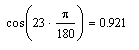
Задание
Вычислить sin(x), cos(x), tg(x), ctg(x)
| Вариант | Значение аргумента в градусах | Функция и аргумент в градусах |
| 1 | 25; 78; -235, 75, 69 | 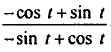 t =21 t =21 |
| 2 | 14; -56, 237, 75, -96 | 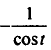 t =67 t =67 |
| 3 | 78; 36; 34; 72; 456 | |
| 4 | 136; 726; 65; 987; -45 | |
| 5 | 367; 125; -165; 264; 341 | 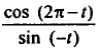 t=97 t=97 |
| 6 | 136; -42; 67; 137; 69 | |
| 7 | 346; 36; 978; 36; 346 | |
| 8 | 346; 642; 134; -42; -67 | |
| 9 | 136; -426; 65; 49; 66 | |
| 10 | 137; -76; -82; 94; 43 | 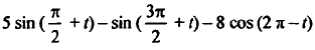 t=79 t=79 |
| 11 | 346; -436; 234; 57; 46 | |
| 12 | 136; 461; 222; 27; 64 | |
Задание 4
Выполнить вычисления с использованием мастера функций:
Пример:
Вычислить
Решение
С помощью главного меню Insert/Function
Вставить функцию:
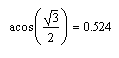
| Вариант | Задание | Задание |
| 1 | | |
| 2 | 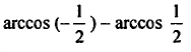 | |
| 3 | 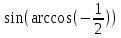 | |
| 4 | 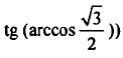 |  |
| 5 | | |
| 6 | | 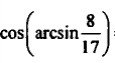 |
| 7 | | |
| 8 | 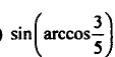 | 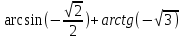 |
| 9 | | 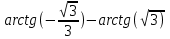 |
| 10 | 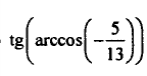 | 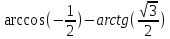 |
| 11 | 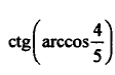 | 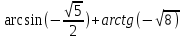 |
| 12 | 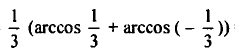 | 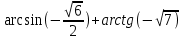 |
Задание 5.
Вычислить
| Вариант | Задание | Задание |
| 1 | log2 sin 225°; | 2 |
| 2 | log3 tg 225°; | 3 ; |
| 3 | 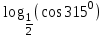 | 5 ; |
| 4 | log5 ctg 495°; | 49 |
| 5 | log4 sin π/4; | 25 ; |
| 6 | log10 tg π/4 ; | 64 |
| 7 | log8 sin 150°; | 3 ; |
| 8 | log2 cos 120°; | 2 ; |
| 9 | log2 sin π/2 — tg π/4; | 4 ; |
| 10 | log3 1 — log4 ctg π/4 • log5 cos 0. | 2 ; |
| 11 | log2 sin π/6— log√3 tg π/6; | 1,5 ; |
| 12 | 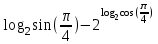 | 5 |
Контрольные вопросы:
-
С помощью какого оператора можно вычислить выражение? -
Как вставить текстовую область в документ Mathcad? -
Чем отличается глобальное и локальное определение переменных? С помощью каких операторов определяются? -
Как изменить формат чисел для всего документа? -
Как изменить формат чисел для отдельного выражения? -
Какие системные (предопределенные) переменные Вам известны? Как узнать их значение? Как изменить их значение? -
Какие виды функций в Mathcad Вам известны? -
Как вставить встроенную функцию в документ Mathcad?
Практитческая работа 2
Тема: Построение и редактирование двумерных графиков в MathCAD.
Цель: освоить приемы построения и форматирования двумерных графиков в MathCAD.
Порядок выполнения работы:
-
Изучить основные понятия и термины, принятые в MathCAD. -
Изучить пользовательский интерфейс MathCAD. -
Выполнить задания. -
Ответить на контрольные вопросы. -
Подготовить отчет о выполнении практической работы.
Общие сведения
В MathCad встроено множество различных математических функций, но пользователь может определять и свои собственные. Вызывается функция посредством ее имени, после которого следуют в круглых скобках аргументы функции (через запятую, если их несколько). Например, после ввода sin()= мы получим значение синуса от радиан, т.е. число 0.
MathCad умеет вычислять значения всех изучаемых в школе функций, в том числе любых тригонометрических: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x) и.т.д. При вычислении тригонометрических функций аргумент указывается в радианах. Так же с его помощью можно получить значения функций: exp(x), ln(x), log(x). Функции можно вводить с клавиатуры, а можно вставлять в выражение с помощью пункта Function … меню Insert или кнопки . С их помощью можно просмотреть список всех встроенных функций MathCad и выбрать необходимую. При наборе имен функций вручную необходимо помнить, что имена встроенных функций не чувствительны к шрифту, но чувствительны к регистру – их следует набирать в точности, как они описаны.
Определение функции пользователя:
<имя функции> (<список аргументов>) <оператор присваивания> <выражение>
Тип аргумента не указывается, а распознается системой при вызове функции. Аргументы могут быть скалярами, матрицами, функциями.
Для задания функций более сложной структуры используют подпрограммы.
Следует знать, что если в определении функции используется имя переменной, которая отсутствует в списке аргументов, тогда это имя должно быть определено перед определением функции. Значение этой переменной в момент ввода определения функции становится постоянной частью функции и изменение значения такой переменной в дальнейшем (до нового вызова функции) не отразится на значении функции.
MathCad позволяет строить графики нескольких типов: в прямоугольной и полярной системах координат, графики поверхностей, контурные и точечные графики, векторные поля, трехмерные графики и гистограммы. Для начального построения графика того или иного вида достаточно задать тип графика. Появится шаблон графика, представляющий собой прямоугольник с пустыми полями для ввода данных.
Построение двумерных графиков
Для наиболее распространенных графиков в декартовой системе координат MathCad предусматривает два способа построения графиков функций одной переменной
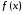 ;
;-
упрощенный способ без задания дискретной переменной x(пределы изменения аргумента x автоматически задаются от –10 до 10); -
обычный способ с заданием дискретной переменной x.
График функции в MathCad строится следующим образом:
-
Определяем функцию; -
В виде дискретной переменной определяем аргумент функции; -
Щелкаем мышкой на том месте, где нужно нарисовать график; -
Выбираем пункт Graph из меню Insert (или щелкаем на панели математических знаков на кнопке с изображением графика) — на экране появится палитра графиков. Выбираем нужный нам шаблон; -
Заполняем пустые поля на шаблоне графика; -
Для получения изображения самого графика щелкаем мышкой вне графика.
Задание 1.
Построить график в декартовых координатах X-Y следующих функций.
Пример:
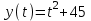
По умолчанию, если не задан интервал изменения аргумента, график функции строится на интервале [0,10].
-
Записать
-
Нажать кнопку на панели инструментов вывод панели Graph, выбрать двумерный график
3. В появившемся шаблоне внизу ввести имя аргумента t, слева имя функции y
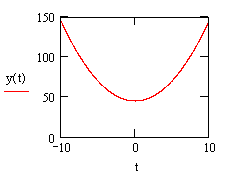
y
