ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 95
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
12 /34...N
R12
, (3)
 где Rij- алгебраическое дополнение соответствующего элемента матрицы R.
где Rij- алгебраическое дополнение соответствующего элемента матрицы R.Например, если 12/34...N=0,8; а 12 = 0,2, значит влияние остальных величин ослабляет зависимость между X1 и X2 .
-
множественный коэффициент корреляции 1/23...Nхарактеризует тесноту
 линейной связи между Х1и остальными переменными, входящими в модель.
линейной связи между Х1и остальными переменными, входящими в модель.1/23...N
, |R| detR
(4)
-
????????
парныйкоэффициентдетерминации????2 - доля вариации случайной величины Xi
, обусловленная вариацией величины Xj.
????2 = ????2 = Объясненная вариация, связанная с ????2)
(5)
12 12
Общая вариация
-
1/23..????
множественныйкоэффициентдетерминации????2 - характеризует долю вариации (дисперсии) X1 , объясняемую влиянием X2 ,X3 ,...,XN, т.е. факторами, входящими в модель.
????2 = ????2
1/23..???? 1/23...????
норм
У показателя ????2 есть недостаток, состоящий в том, что большие значения коэффициента детерминации могут достигаться благодаря малому числу наблюдений. Нормированный ????2 обеспечивает информацией о том, какое значение вы могли бы получить в другом наборе данных значительно большего объема, чем в данном случае.

????2 = 1 − (1 − ????2 ) ????−1 ,
норм
????−????−1
где k– количество факторных переменных.
Примеррешениязадачи1.
Решим задачу: На основании выборочных данных по 20 туристическим фирмам о затратах на рекламу (Х) и количества туристов, воспользовавшихся услугами фирмы (Y), представленных в таблице, определите коэффициента парной корреляции и его значимость. Уровень значимости равен 5%.
| X | 8,1 | 8,2 | 8,6 | 9,2 | 9,4 | 9,5 | 9,8 | 9,9 | 10,1 | 10,3 |
| Y | 800 | 850 | 720 | 850 | 800 | 880 | 950 | 820 | 900 | 1000 |
| X | 10,4 | 10,5 | 10,6 | 11,2 | 11,3 | 11,7 | 11,9 | 12,4 | 12,5 | 12,7 |
| Y | 920 | 1060 | 950 | 900 | 1200 | 1150 | 1000 | 1200 | 1100 | 1000 |
Решение:
-
Коэффициенткорреляции.Предполагаем, что количество туристов, воспользовавшихся услугами фирмы (Y), зависят от затрат на рекламу (Х), тогда строим модель ????̃=f(X). Средствами MS Excel данную задачу можно решить с помощью статистических функций:
rxy КОРРЕЛ(массив X, массив Y)=0,794.
-
Значимость коэффициентов. Определим значимость коэффициента корреляции:
????0: ???? = 0

набл
???? = ????
√1−????2
√???? − 2 = 0,794

 √1−0,7942
√1−0,7942
√20 − 2 = 5,543
???????????? = ????????−1(????, ???? − 2) =СТЬЮДРАСПОБР(0,05;20-2)=2,1, т.к. |????набл| > ????????????, то коэффициент корреляции значим и между случайными величинами Х и Y существует статистическая связь.
Определим значимость коэффициента регрессии:


????0: ???????????? = 0
(????−1)⋅????2 (20−1)⋅1,3852
????2
 ????набл= ????????????√???? = 78,08√
????набл= ????????????√???? = 78,08√ ????
85,062
= 5,542,
???????????? = ????????−1(????, ???? − 2) =СТЬЮДРАСПОБР1(0,05;20-2)=2,1, т.к. |????набл| > ????????????, то коэффициент регресии значим и модель регрессии значимо описывает экспериментальные данные.
Примеррешениязадачи2.
Решимзадачу:Для вычисления взаимозависимости между себестоимостью 1т песка (Z), сменной добычей песка (Y) и фондоотдачей (Х) было обследовано 8 карьеров. В результате получены следующие данные:
| X | 30 | 20 | 40 | 35 | 45 | 25 | 50 | 30 |
| Y | 20 | 30 | 50 | 70 | 80 | 20 | 90 | 25 |
| Z | 20 | 25 | 20 | 15 | 10 | 30 | 10 | 20 |
Вычислить а) матрицу выборочных парных коэффициентов корреляции и проверить их значимость при =5%.
Решение:
а) Для получения корреляционной матрицы воспользуемся макрофункцией
«Корреляция» пакета «Анализ данных». Введем во входной интервал массив данных, включая названия строк, например, (А1:I3). Отметим, что группирование идет по строкам, и поставим флажок в графе «Метки в первом столбце». Укажем имя левой верхней ячейке в графе «Выходной интервал» (рис. 1.).
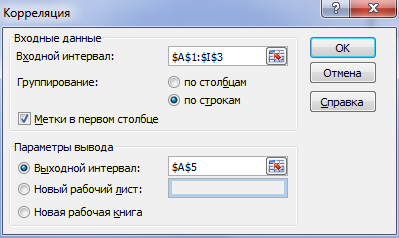
Рис. 1. Макрофункция «Корреляция».
Выходная область (А5:D8) содержит корреляционную матрицу (рис. 2.). Т.к. корреляционная матрица симметрична относительно главной диагонали, то можно треугольную матрицу достроить симметрично главной диагонали.
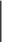 1 0,871
1 0,871R 0,871 1
0,874
 0,879
0,879 0,874 0,879 1
 1 СТЬЮДРАСПОБР(α;n-2)=СТЬЮДЕНТ.ОБР.2Х(α;n-2)
1 СТЬЮДРАСПОБР(α;n-2)=СТЬЮДЕНТ.ОБР.2Х(α;n-2)
Рис. 2. Корреляционная матрица
Для определения значимости парных коэффициентов корреляции воспользуемся формулами задачи 1 или определим коэффициент парной корреляции, начиная с которого будет выполняться неравенство:|????набл| > ???????????? = ????????−1(????, ???? − ????). Вычислим tнабл по формуле аналогично задаче 1 относительно произвольного коэффициента корреляции и найдем
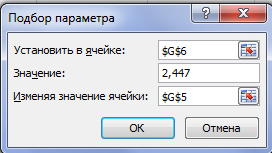 ???????????? = ????????−1(????, ???? − ????) = СТЬЮДРАСПОБР(0,05; 8 − 2) = 2,447 (рис. 3). С помощью функции «Подбор параметра» (рис. 3) найдем минимальное значение парного коэффициента корреляции, начиная с которого все парные коэффициенты корреляции будут значимы.
???????????? = ????????−1(????, ???? − ????) = СТЬЮДРАСПОБР(0,05; 8 − 2) = 2,447 (рис. 3). С помощью функции «Подбор параметра» (рис. 3) найдем минимальное значение парного коэффициента корреляции, начиная с которого все парные коэффициенты корреляции будут значимы.Рис. 3. Нахождение минимального значимого парного коэффициента корреляции Минимальное значение парного коэффициента получилось равным 0,707, значит все
элементы корреляционной матрицы, стоящие вне главной диагонали, больше этого значения являются значимыми. Для наглядности выделим значимые коэффициенты корреляции жирным шрифтом (рис. 2).
2. Регрессионный анализ.
Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных X j(j=1,2,...k), рассматриваемых в регрессионном анализе как kнеслучайных величин, независимо от истинного закона распределения Xj .
Y
Обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием
(X1,X2 ,...,Xk),
являющимся функцией от аргументов Xj, и постоянной, не зависящей от аргументов
дисперсией 2 . Пусть из генеральной совокупности (Y,X1 ,X2 ,...,Xk)
берется выборка
Y
объемом n(yi,x1i,x2i,...,xkn)i 1,k. Требуется по выборке найти оценку уравнений регрессии (X1,X2 ,...,Xk)и исследовать его свойства.
Вид функции выбирают заранее, наиболее часто встречающиеся:
Y
Линейная 0 1X1 2 X2 ...kXk;
-
Полиномиальная X X2 ... Xk;
Y 0 1 2 k
-
Степенная (логарифмически-линейная)
X1 X2 ...XK
Y 0 1 2 k
Линейная двумерная модель.
Необходимо найти оценку двумерного линейного уравнения регрессии:
Y 0 1X y b0 b1x ei. (1)
Для оценки неизвестных параметров 0 и 1 из двумерной генеральной
совокупности (X,Y)
берется выборка объемом n, где ( yi,xi)
-
результат i-того
наблюдения ( i 1,2,...,n). Оценку 0 и 1 производится с помощью метода наименьших квадратов (МНК).
Согласно МНК, в качестве оценок неизвестных параметров 0 и 1 следует брать
такие значения выборочных характеристик b0 и b1 , которые минимизируют сумму квадратов отклонений:
n
Q (y b
bx)2 min.
i 0 1 i
i1 0 1
Исследуя функцию Qна минимум, получим:
Q 0
Q
2(y b bx) 0
b
b
i 0 1 i
b0n b1 xi yi
0
0
2
(2)
Q 0
Q 2(y b
-
bx)x 0
b0 xi b1 xi
yixi
b
b
i 0 1 i i
1 1
i i i i;
Решая эту систему уравнений, например, методом Крамера получаем:
b0
yi x2 x xy
b1
nxiyixiyi
(3)
i i
i i
n x2 ( x)2 n x2 ( x)2
????
Оценка ????2 остаточной дисперсии 2 имеет вид:
????2 = 1
∑????
(????
− ????
− ???? ???? )2
(4)
 ???? ????−2
???? ????−2
????=1 ????
0 1 ????
Проверказначимостиинахождениеинтервальныхоценоккоэффициентов
регрессии
-
Для проверки соответствия уравнения регрессии экспериментальным данным.
В MS Excel для этих целей рассчитывается Значимость F. Если Значимость F < α. принятого в задаче, то модель соответствует экспериментальным данным.
-
Для проверки значимости коэффициентов регрессии
В MS Excel для этих целей рассчитывается P-значение. Если Р-значение < α. принятого в задаче, то коэффициент регрессии значим.
Если значим коэффициент регрессии b1, то значимо и уравнение регрессии.
Линейная множественная модель.
Рассмотрим общий случай линейной регрессии, когда условное математическое
Y
ожидание есть функция kпеременных:
Y
0 1X1 2 X2 ...kXk.
В матричном виде это уравнение примет вид: Y X , где Y- вектор-столбец наблюдений
размерности ( n 1); X- матрица факторных признаков размерности ( n ( k 1)); - вектор неизвестных параметров размерности ((k 1) 1).
Оценка МНК вектора имеет вид:
b XT X1 XT Y,
где XT- транспонированная матрица Х, XT X1 - матрица, обратная матрице
XT X.
Несмещенная оценка остаточной дисперсии:
????2 = 1
(???? − ????????)????(???? − ????????),
 ???? ????−????−1
???? ????−????−1
Примеррешениязадачилинейнойдвумернойрегрессии
На основании выборочных данных по 20 туристическим фирмам о затратах на рекламу (Х) и количества туристов, воспользовавшихся услугами фирмы (Y), представленных в таблице, вычислить статистические характеристики двумерной линейной регрессионной модели. Определите соответствие модели экспериментальным данным и значимость регрессионной модели. Определите доверительные интервалы коэффициентов регрессии. Уровень значимости равен 5%.
X
8,1
8,2
8,6
9,2
9,4
9,5
9,8
9,9
10,1
10,3
Y
800
850
720
850
800
880
950
820
900
1000
X
10,4
10,5
10,6
11,2
11,3
11,7
11,9
12,4
12,5
12,7
Y
920
1060
950
900
1200
1150
1000
1200
1100
1000
Решение:
Построение уравнения линейной регрессии. Для построения линейной регрессии воспользуемся макрофункцией Регрессия (рис. 1). Для макрофункции Регрессия важно, чтобы группирование переменных было по столбцам.
Входные интервалы переменных Х и Y вводим вместе с названиями и ставим флажок в поле Метки, чтобы показать, что в первой строке стоят названия переменных. Отмечаем выходной интервал и ставим флажок в графике подбора, на котором отображается корреляционное поле, включающее экспериментальные данные и регрессионную модель.

Рис. 1. Макрофункция Регрессия.
Выходной интервал содержит 3 таблицы (рис. 2). В первой таблице отражается коэффициент корреляции ρ, коэффициент детерминации R2, нормированный коэффициент
детерминации ????2 и стандартная ошибка ???? .
норм ????
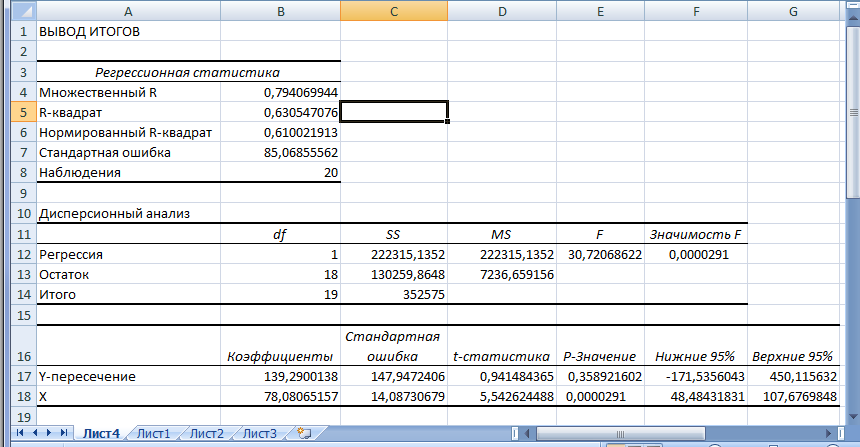
Рис. 2. Нахождение линейной регрессии.
Во второй таблице проводится анализ соответствия модели экспериментальным данным. В третьей таблице представлена информация о коэффициентах регрессии, их значимости и доверительных интервалах.
Выводы:
-
норм
????2 <0.7 связь между переменными слабая.
????е=85,07.
-
Значимость F< 0,05, следовательно, модель соответствует экспериментальным данным.
-
Р-значение для коэффициента b0 больше α=0,05, следовательно, коэффициент незначим. Р-значение для коэффициента b1 меньше α=0,05, следовательно, коэффициент значим. Значимость коэффициента b1 свидетельствует о значимости регрессионной модели.
-
Уравнение регрессии имеет вид: ????̃ = 139,29 + 78,08????
Доверительные интервалы ????0 ∈ [−171,54; 450,11] и ????1 ∈ [48,48; 107,68]
Примеррешениязадачимножественной линейнойрегрессии.
В таблице приведены результаты работы 27 предприятий:
2. Регрессионный анализ.
Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных X j(j=1,2,...k), рассматриваемых в регрессионном анализе как kнеслучайных величин, независимо от истинного закона распределения Xj .
Y
Обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием
(X1,X2 ,...,Xk),
являющимся функцией от аргументов Xj, и постоянной, не зависящей от аргументов
дисперсией 2 . Пусть из генеральной совокупности (Y,X1 ,X2 ,...,Xk)
берется выборка
Y
объемом n(yi,x1i,x2i,...,xkn)i 1,k. Требуется по выборке найти оценку уравнений регрессии (X1,X2 ,...,Xk)и исследовать его свойства.
Вид функции выбирают заранее, наиболее часто встречающиеся:
Y
Линейная 0 1X1 2 X2 ...kXk;
-
Полиномиальная X X2 ... Xk;
Y 0 1 2 k
-
Степенная (логарифмически-линейная)
X1 X2 ...XK
Y 0 1 2 k
Линейная двумерная модель.
Необходимо найти оценку двумерного линейного уравнения регрессии:
Y 0 1X y b0 b1x ei. (1)
Для оценки неизвестных параметров 0 и 1 из двумерной генеральной
совокупности (X,Y)
берется выборка объемом n, где ( yi,xi)
-
результат i-того
наблюдения ( i 1,2,...,n). Оценку 0 и 1 производится с помощью метода наименьших квадратов (МНК).
Согласно МНК, в качестве оценок неизвестных параметров 0 и 1 следует брать
такие значения выборочных характеристик b0 и b1 , которые минимизируют сумму квадратов отклонений:
n
Q (y b
bx)2 min.
i 0 1 i
i1 0 1
Исследуя функцию Qна минимум, получим:
Q 0
Q
2(y b bx) 0
b
b
i 0 1 i
b0n b1 xi yi
0
0
2
(2)
Q 0
Q 2(y b
-
bx)x 0
b0 xi b1 xi
yixi
b
b
i 0 1 i i
1 1
i i i i;
Решая эту систему уравнений, например, методом Крамера получаем:
b0
yi x2 x xy
b1
nxiyixiyi
(3)
i i
i i
n x2 ( x)2 n x2 ( x)2
????
Оценка ????2 остаточной дисперсии 2 имеет вид:
????2 = 1
∑????
(????
− ????
− ???? ???? )2
(4)
 ???? ????−2
???? ????−2
????=1 ????
0 1 ????
Проверказначимостиинахождениеинтервальныхоценоккоэффициентов
регрессии
-
Для проверки соответствия уравнения регрессии экспериментальным данным.
В MS Excel для этих целей рассчитывается Значимость F. Если Значимость F < α. принятого в задаче, то модель соответствует экспериментальным данным.
-
Для проверки значимости коэффициентов регрессии
В MS Excel для этих целей рассчитывается P-значение. Если Р-значение < α. принятого в задаче, то коэффициент регрессии значим.
Если значим коэффициент регрессии b1, то значимо и уравнение регрессии.
Линейная множественная модель.
Рассмотрим общий случай линейной регрессии, когда условное математическое
Y
ожидание есть функция kпеременных:
Y
0 1X1 2 X2 ...kXk.
В матричном виде это уравнение примет вид: Y X , где Y- вектор-столбец наблюдений
размерности ( n 1); X- матрица факторных признаков размерности ( n ( k 1)); - вектор неизвестных параметров размерности ((k 1) 1).
Оценка МНК вектора имеет вид:
b XT X1 XT Y,
где XT- транспонированная матрица Х, XT X1 - матрица, обратная матрице
XT X.
Несмещенная оценка остаточной дисперсии:
????2 = 1
(???? − ????????)????(???? − ????????),
 ???? ????−????−1
???? ????−????−1
Примеррешениязадачилинейнойдвумернойрегрессии
На основании выборочных данных по 20 туристическим фирмам о затратах на рекламу (Х) и количества туристов, воспользовавшихся услугами фирмы (Y), представленных в таблице, вычислить статистические характеристики двумерной линейной регрессионной модели. Определите соответствие модели экспериментальным данным и значимость регрессионной модели. Определите доверительные интервалы коэффициентов регрессии. Уровень значимости равен 5%.
X
8,1
8,2
8,6
9,2
9,4
9,5
9,8
9,9
10,1
10,3
Y
800
850
720
850
800
880
950
820
900
1000
X
10,4
10,5
10,6
11,2
11,3
11,7
11,9
12,4
12,5
12,7
Y
920
1060
950
900
1200
1150
1000
1200
1100
1000
Решение:
Построение уравнения линейной регрессии. Для построения линейной регрессии воспользуемся макрофункцией Регрессия (рис. 1). Для макрофункции Регрессия важно, чтобы группирование переменных было по столбцам.
Входные интервалы переменных Х и Y вводим вместе с названиями и ставим флажок в поле Метки, чтобы показать, что в первой строке стоят названия переменных. Отмечаем выходной интервал и ставим флажок в графике подбора, на котором отображается корреляционное поле, включающее экспериментальные данные и регрессионную модель.

Рис. 1. Макрофункция Регрессия.
Выходной интервал содержит 3 таблицы (рис. 2). В первой таблице отражается коэффициент корреляции ρ, коэффициент детерминации R2, нормированный коэффициент
детерминации ????2 и стандартная ошибка ???? .
норм ????

Рис. 2. Нахождение линейной регрессии.
Во второй таблице проводится анализ соответствия модели экспериментальным данным. В третьей таблице представлена информация о коэффициентах регрессии, их значимости и доверительных интервалах.
Выводы:
-
норм
????2 <0.7 связь между переменными слабая.
????е=85,07.
-
Значимость F< 0,05, следовательно, модель соответствует экспериментальным данным.
-
Р-значение для коэффициента b0 больше α=0,05, следовательно, коэффициент незначим. Р-значение для коэффициента b1 меньше α=0,05, следовательно, коэффициент значим. Значимость коэффициента b1 свидетельствует о значимости регрессионной модели.
-
Уравнение регрессии имеет вид: ????̃ = 139,29 + 78,08????
Доверительные интервалы ????0 ∈ [−171,54; 450,11] и ????1 ∈ [48,48; 107,68]
Примеррешениязадачимножественной линейнойрегрессии.
В таблице приведены результаты работы 27 предприятий:
2. Регрессионный анализ.
Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных X j(j=1,2,...k), рассматриваемых в регрессионном анализе как kнеслучайных величин, независимо от истинного закона распределения Xj .
Y
Обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием
(X1,X2 ,...,Xk),
являющимся функцией от аргументов Xj, и постоянной, не зависящей от аргументов
дисперсией 2 . Пусть из генеральной совокупности (Y,X1 ,X2 ,...,Xk)
берется выборка
Y
объемом n(yi,x1i,x2i,...,xkn)i 1,k. Требуется по выборке найти оценку уравнений регрессии (X1,X2 ,...,Xk)и исследовать его свойства.
Вид функции выбирают заранее, наиболее часто встречающиеся:
Y
Линейная 0 1X1 2 X2 ...kXk;
-
Полиномиальная X X2 ... Xk;
Y 0 1 2 k
-
Степенная (логарифмически-линейная)
X1 X2 ...XK
Y 0 1 2 k
Линейная двумерная модель.
Необходимо найти оценку двумерного линейного уравнения регрессии:
Y 0 1X y b0 b1x ei. (1)
Для оценки неизвестных параметров 0 и 1 из двумерной генеральной
совокупности (X,Y)
берется выборка объемом n, где ( yi,xi)
-
результат i-того
наблюдения ( i 1,2,...,n). Оценку 0 и 1 производится с помощью метода наименьших квадратов (МНК).
Согласно МНК, в качестве оценок неизвестных параметров 0 и 1 следует брать
такие значения выборочных характеристик b0 и b1 , которые минимизируют сумму квадратов отклонений:
n
Q (y b
bx)2 min.
i 0 1 i
i1 0 1
Исследуя функцию Qна минимум, получим:
Q 0
Q
2(y b bx) 0
b
b
i 0 1 i
b0n b1 xi yi
0
0
2
(2)
Q 0
Q 2(y b
-
bx)x 0
b0 xi b1 xi
yixi
b
b
i 0 1 i i
1 1
i i i i;
Решая эту систему уравнений, например, методом Крамера получаем:
b0
yi x2 x xy
b1
nxiyixiyi
(3)
i i
i i
n x2 ( x)2 n x2 ( x)2
????
Оценка ????2 остаточной дисперсии 2 имеет вид:
????2 = 1
∑????
(????
− ????
− ???? ???? )2
(4)
 ???? ????−2
???? ????−2
????=1 ????
0 1 ????
Проверказначимостиинахождениеинтервальныхоценоккоэффициентов
регрессии
-
Для проверки соответствия уравнения регрессии экспериментальным данным.
В MS Excel для этих целей рассчитывается Значимость F. Если Значимость F < α. принятого в задаче, то модель соответствует экспериментальным данным.
-
Для проверки значимости коэффициентов регрессии
В MS Excel для этих целей рассчитывается P-значение. Если Р-значение < α. принятого в задаче, то коэффициент регрессии значим.
Если значим коэффициент регрессии b1, то значимо и уравнение регрессии.
Линейная множественная модель.
Рассмотрим общий случай линейной регрессии, когда условное математическое
Y
ожидание есть функция kпеременных:
Y
0 1X1 2 X2 ...kXk.
В матричном виде это уравнение примет вид: Y X , где Y- вектор-столбец наблюдений
размерности ( n 1); X- матрица факторных признаков размерности ( n ( k 1)); - вектор неизвестных параметров размерности ((k 1) 1).
Оценка МНК вектора имеет вид:
b XT X1 XT Y,
где XT- транспонированная матрица Х, XT X1 - матрица, обратная матрице
XT X.
Несмещенная оценка остаточной дисперсии:
????2 = 1
(???? − ????????)????(???? − ????????),
 ???? ????−????−1
???? ????−????−1
Примеррешениязадачилинейнойдвумернойрегрессии
На основании выборочных данных по 20 туристическим фирмам о затратах на рекламу (Х) и количества туристов, воспользовавшихся услугами фирмы (Y), представленных в таблице, вычислить статистические характеристики двумерной линейной регрессионной модели. Определите соответствие модели экспериментальным данным и значимость регрессионной модели. Определите доверительные интервалы коэффициентов регрессии. Уровень значимости равен 5%.
X
8,1
8,2
8,6
9,2
9,4
9,5
9,8
9,9
10,1
10,3
Y
800
850
720
850
800
880
950
820
900
1000
X
10,4
10,5
10,6
11,2
11,3
11,7
11,9
12,4
12,5
12,7
Y
920
1060
950
900
1200
1150
1000
1200
1100
1000
Решение:
Построение уравнения линейной регрессии. Для построения линейной регрессии воспользуемся макрофункцией Регрессия (рис. 1). Для макрофункции Регрессия важно, чтобы группирование переменных было по столбцам.
Входные интервалы переменных Х и Y вводим вместе с названиями и ставим флажок в поле Метки, чтобы показать, что в первой строке стоят названия переменных. Отмечаем выходной интервал и ставим флажок в графике подбора, на котором отображается корреляционное поле, включающее экспериментальные данные и регрессионную модель.

Рис. 1. Макрофункция Регрессия.
Выходной интервал содержит 3 таблицы (рис. 2). В первой таблице отражается коэффициент корреляции ρ, коэффициент детерминации R2, нормированный коэффициент
детерминации ????2 и стандартная ошибка ???? .
норм ????

Рис. 2. Нахождение линейной регрессии.
Во второй таблице проводится анализ соответствия модели экспериментальным данным. В третьей таблице представлена информация о коэффициентах регрессии, их значимости и доверительных интервалах.
Выводы:
-
норм
????2 <0.7 связь между переменными слабая.
????е=85,07.
-
Значимость F< 0,05, следовательно, модель соответствует экспериментальным данным.
-
Р-значение для коэффициента b0 больше α=0,05, следовательно, коэффициент незначим. Р-значение для коэффициента b1 меньше α=0,05, следовательно, коэффициент значим. Значимость коэффициента b1 свидетельствует о значимости регрессионной модели.
-
Уравнение регрессии имеет вид: ????̃ = 139,29 + 78,08????
Доверительные интервалы ????0 ∈ [−171,54; 450,11] и ????1 ∈ [48,48; 107,68]
Примеррешениязадачимножественной линейнойрегрессии.
В таблице приведены результаты работы 27 предприятий:
2. Регрессионный анализ.
Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных X j(j=1,2,...k), рассматриваемых в регрессионном анализе как kнеслучайных величин, независимо от истинного закона распределения Xj .
Y
Обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием
(X1,X2 ,...,Xk),
являющимся функцией от аргументов Xj, и постоянной, не зависящей от аргументов
дисперсией 2 . Пусть из генеральной совокупности (Y,X1 ,X2 ,...,Xk)
берется выборка
Y
объемом n(yi,x1i,x2i,...,xkn)i 1,k. Требуется по выборке найти оценку уравнений регрессии (X1,X2 ,...,Xk)и исследовать его свойства.
Вид функции выбирают заранее, наиболее часто встречающиеся:
Y
Линейная 0 1X1 2 X2 ...kXk;
-
Полиномиальная X X2 ... Xk;
Y 0 1 2 k
-
Степенная (логарифмически-линейная)
X1 X2 ...XK
Y 0 1 2 k
Линейная двумерная модель.
Необходимо найти оценку двумерного линейного уравнения регрессии:
2. Регрессионный анализ.
Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных X j(j=1,2,...k), рассматриваемых в регрессионном анализе как kнеслучайных величин, независимо от истинного закона распределения Xj .
Y
Обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием
(X1,X2 ,...,Xk), являющимся функцией от аргументов Xj, и постоянной, не зависящей от аргументов
дисперсией 2 . Пусть из генеральной совокупности (Y,X1 ,X2 ,...,Xk)
берется выборка
Y
объемом n(yi,x1i,x2i,...,xkn)i 1,k. Требуется по выборке найти оценку уравнений регрессии (X1,X2 ,...,Xk)и исследовать его свойства.
Вид функции выбирают заранее, наиболее часто встречающиеся:
Y
Линейная 0 1X1 2 X2 ...kXk;
-
Полиномиальная X X2 ... Xk;
Y 0 1 2 k
-
Степенная (логарифмически-линейная)
Y 0 1X y b0 b1x ei. (1)
Для оценки неизвестных параметров 0 и 1 из двумерной генеральной
совокупности (X,Y)
берется выборка объемом n, где ( yi,xi)
-
результат i-того
наблюдения ( i 1,2,...,n). Оценку 0 и 1 производится с помощью метода наименьших квадратов (МНК).
Согласно МНК, в качестве оценок неизвестных параметров 0 и 1 следует брать
такие значения выборочных характеристик b0 и b1 , которые минимизируют сумму квадратов отклонений:
n
Q (y b
bx)2 min.
i 0 1 i
i1 0 1
Исследуя функцию Qна минимум, получим:
Q 0
Q
2(y b bx) 0
b
b
i 0 1 i
b0n b1 xi yi
0
0
2
(2)
Q 0
Q 2(y b
-
bx)x 0
b0 xi b1 xi
yixi
b
b
i 0 1 i i
1 1
i i i i;
Решая эту систему уравнений, например, методом Крамера получаем:
b0
yi x2 x xy
b1
nxiyixiyi
(3)
i i
i i
n x2 ( x)2 n x2 ( x)2
????
Оценка ????2 остаточной дисперсии 2 имеет вид:
????2 = 1
∑????
(????
− ????
− ???? ???? )2
(4)
 ???? ????−2
???? ????−2????=1 ????
0 1 ????
Проверказначимостиинахождениеинтервальныхоценоккоэффициентов
регрессии
-
Для проверки соответствия уравнения регрессии экспериментальным данным.
В MS Excel для этих целей рассчитывается Значимость F. Если Значимость F < α. принятого в задаче, то модель соответствует экспериментальным данным.
-
Для проверки значимости коэффициентов регрессии
В MS Excel для этих целей рассчитывается P-значение. Если Р-значение < α. принятого в задаче, то коэффициент регрессии значим.
Если значим коэффициент регрессии b1, то значимо и уравнение регрессии.
Линейная множественная модель.
Рассмотрим общий случай линейной регрессии, когда условное математическое
Y
ожидание есть функция kпеременных:
Y
0 1X1 2 X2 ...kXk.
В матричном виде это уравнение примет вид: Y X , где Y- вектор-столбец наблюдений
размерности ( n 1); X- матрица факторных признаков размерности ( n ( k 1)); - вектор неизвестных параметров размерности ((k 1) 1).
Оценка МНК вектора имеет вид:
b XT X1 XT Y,
где XT- транспонированная матрица Х, XT X1 - матрица, обратная матрице
XT X.
Несмещенная оценка остаточной дисперсии:
????2 = 1
(???? − ????????)????(???? − ????????),
 ???? ????−????−1
???? ????−????−1Примеррешениязадачилинейнойдвумернойрегрессии
На основании выборочных данных по 20 туристическим фирмам о затратах на рекламу (Х) и количества туристов, воспользовавшихся услугами фирмы (Y), представленных в таблице, вычислить статистические характеристики двумерной линейной регрессионной модели. Определите соответствие модели экспериментальным данным и значимость регрессионной модели. Определите доверительные интервалы коэффициентов регрессии. Уровень значимости равен 5%.
| X | 8,1 | 8,2 | 8,6 | 9,2 | 9,4 | 9,5 | 9,8 | 9,9 | 10,1 | 10,3 |
| Y | 800 | 850 | 720 | 850 | 800 | 880 | 950 | 820 | 900 | 1000 |
| X | 10,4 | 10,5 | 10,6 | 11,2 | 11,3 | 11,7 | 11,9 | 12,4 | 12,5 | 12,7 |
| Y | 920 | 1060 | 950 | 900 | 1200 | 1150 | 1000 | 1200 | 1100 | 1000 |
Решение:
Построение уравнения линейной регрессии. Для построения линейной регрессии воспользуемся макрофункцией Регрессия (рис. 1). Для макрофункции Регрессия важно, чтобы группирование переменных было по столбцам.
Входные интервалы переменных Х и Y вводим вместе с названиями и ставим флажок в поле Метки, чтобы показать, что в первой строке стоят названия переменных. Отмечаем выходной интервал и ставим флажок в графике подбора, на котором отображается корреляционное поле, включающее экспериментальные данные и регрессионную модель.

Рис. 1. Макрофункция Регрессия.
Выходной интервал содержит 3 таблицы (рис. 2). В первой таблице отражается коэффициент корреляции ρ, коэффициент детерминации R2, нормированный коэффициент
детерминации ????2 и стандартная ошибка ???? .
норм ????

Рис. 2. Нахождение линейной регрессии.
Во второй таблице проводится анализ соответствия модели экспериментальным данным. В третьей таблице представлена информация о коэффициентах регрессии, их значимости и доверительных интервалах.
Выводы:
-
норм
????2 <0.7 связь между переменными слабая.
????е=85,07.
-
Значимость F< 0,05, следовательно, модель соответствует экспериментальным данным. -
Р-значение для коэффициента b0 больше α=0,05, следовательно, коэффициент незначим. Р-значение для коэффициента b1 меньше α=0,05, следовательно, коэффициент значим. Значимость коэффициента b1 свидетельствует о значимости регрессионной модели. -
Уравнение регрессии имеет вид: ????̃ = 139,29 + 78,08????
Доверительные интервалы ????0 ∈ [−171,54; 450,11] и ????1 ∈ [48,48; 107,68]
Примеррешениязадачимножественной линейнойрегрессии.
В таблице приведены результаты работы 27 предприятий:
| Х1 | 195 | 120 | 150 | 170 | 140 | 160 | 158 | 178 | 148 | 155 | 140 | 165 | 155 |
| Х2 | 135 | 75 | 81 | 138 | 123 | 116 | 119 | 112 | 128 | 116 | 125 | 114 | 128 |
| Y | 107 | 67 | 81 | 93 | 81 | 86 | 86 | 96 | 80 | 86 | 78 | 89 | 84 |


