Файл: Варианты контрольной работы.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.05.2024

Просмотров: 132

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Варианты контрольной работы

Примеры решения задач

2. Регрессионный анализ. Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных X j(j=1,2,...k), рассматриваемых в регрессионном анализе как kнеслучайных величин, независимо от истинного закона распределения Xj . YОбычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием  (X1,X2 ,...,Xk), являющимся функцией от аргументов Xj, и постоянной, не зависящей от аргументов дисперсией 2 . Пусть из генеральной совокупности (Y,X1 ,X2 ,...,Xk)берется выборка Yобъемом n(yi,x1i,x2i,...,xkn)i 1,k. Требуется по выборке найти оценку уравнений регрессии  (X1,X2 ,...,Xk)и исследовать его свойства. Вид функции выбирают заранее, наиболее часто встречающиеся: Y Линейная  0 1X1 2 X2 ...kXk; Полиномиальная     X  X2 ... Xk; Y 0 1 2 k Степенная (логарифмически-линейная)    X1  X2 ...XK Y 0 1 2 k Линейная двумерная модель. Необходимо найти оценку двумерного линейного уравнения регрессии:Y 0  1X y b0  b1x ei. (1)Для оценки неизвестных параметров 0 и 1 из двумерной генеральной совокупности (X,Y)берется выборка объемом n, где ( yi,xi) результат i-того наблюдения ( i 1,2,...,n). Оценку 0 и 1 производится с помощью метода наименьших квадратов (МНК).Согласно МНК, в качестве оценок неизвестных параметров 0 и 1 следует братьтакие значения выборочных характеристик b0 и b1 , которые минимизируют сумму квадратов отклонений: nQ (y b bx)2  min.  i 0 1 i  i1 0 1Исследуя функцию Qна минимум, получим:  Q 0 Q 2(y b bx) 0 b bi 0 1 i b0n b1 xi  yi   0  0  2(2)  Q 0Q 2(y b bx)x 0 b0  xi b1 xi  yixi bbi 0 1 i i  1  1 i i i i;Решая эту систему уравнений, например, методом Крамера получаем: b0  yi x2   x xyb1 nxiyixiyi(3) i i i in x2  ( x)2 n x2  ( x)2 ????Оценка ????2 остаточной дисперсии 2 имеет вид: ????2 = 1∑????(????− ????− ???? ???? )2(4) ???? ????−2????=1 ????0 1 ???? Проверказначимостиинахождениеинтервальныхоценоккоэффициентоврегрессии Для проверки соответствия уравнения регрессии экспериментальным данным. В MS Excel для этих целей рассчитывается Значимость F. Если Значимость F < α. принятого в задаче, то модель соответствует экспериментальным данным. Для проверки значимости коэффициентов регрессии В MS Excel для этих целей рассчитывается P-значение. Если Р-значение < α. принятого в задаче, то коэффициент регрессии значим.Если значим коэффициент регрессии b1, то значимо и уравнение регрессии. Линейная множественная модель. Рассмотрим общий случай линейной регрессии, когда условное математическое Y ожидание есть функция kпеременных: Y 0 1X1 2 X2 ...kXk. В матричном виде это уравнение примет вид: Y X , где Y- вектор-столбец наблюденийразмерности ( n  1); X- матрица факторных признаков размерности ( n  ( k  1));  - вектор неизвестных параметров размерности ((k 1) 1).Оценка МНК вектора  имеет вид:b XT X1 XT Y, где XT- транспонированная матрица Х, XT X1 - матрица, обратная матрице XT X.Несмещенная оценка остаточной дисперсии: ????2 = 1(???? − ????????)????(???? − ????????), ???? ????−????−1ПримеррешениязадачилинейнойдвумернойрегрессииНа основании выборочных данных по 20 туристическим фирмам о затратах на рекламу (Х) и количества туристов, воспользовавшихся услугами фирмы (Y), представленных в таблице, вычислить статистические характеристики двумерной линейной регрессионной модели. Определите соответствие модели экспериментальным данным и значимость регрессионной модели. Определите доверительные интервалы коэффициентов регрессии. Уровень значимости равен 5%. X 8,1 8,2 8,6 9,2 9,4 9,5 9,8 9,9 10,1 10,3 Y 800 850 720 850 800 880 950 820 900 1000 X 10,4 10,5 10,6 11,2 11,3 11,7 11,9 12,4 12,5 12,7 Y 920 1060 950 900 1200 1150 1000 1200 1100 1000 Решение:Построение уравнения линейной регрессии. Для построения линейной регрессии воспользуемся макрофункцией Регрессия (рис. 1). Для макрофункции Регрессия важно, чтобы группирование переменных было по столбцам.Входные интервалы переменных Х и Y вводим вместе с названиями и ставим флажок в поле Метки, чтобы показать, что в первой строке стоят названия переменных. Отмечаем выходной интервал и ставим флажок в графике подбора, на котором отображается корреляционное поле, включающее экспериментальные данные и регрессионную модель. Рис. 1. Макрофункция Регрессия.Выходной интервал содержит 3 таблицы (рис. 2). В первой таблице отражается коэффициент корреляции ρ, коэффициент детерминации R2, нормированный коэффициент детерминации ????2 и стандартная ошибка ???? .норм ???? Рис. 2. Нахождение линейной регрессии.Во второй таблице проводится анализ соответствия модели экспериментальным данным. В третьей таблице представлена информация о коэффициентах регрессии, их значимости и доверительных интервалах.Выводы: норм????2 <0.7 связь между переменными слабая.  ????е=85,07. Значимость F< 0,05, следовательно, модель соответствует экспериментальным данным. Р-значение для коэффициента b0 больше α=0,05, следовательно, коэффициент незначим. Р-значение для коэффициента b1 меньше α=0,05, следовательно, коэффициент значим. Значимость коэффициента b1 свидетельствует о значимости регрессионной модели. Уравнение регрессии имеет вид: ????̃ = 139,29 + 78,08????  Доверительные интервалы ????0 ∈ [−171,54; 450,11] и ????1 ∈ [48,48; 107,68]Примеррешениязадачимножественной линейнойрегрессии.В таблице приведены результаты работы 27 предприятий:

3. Задачи линейного программирования.

4. Двойственные задачи линейного программирования

3. Двумерные задачи линейного программирования

Инвестиционный анализ. Сравнение инвестиционных проектов

Практические задания

Регрессионный анализ

Задачи линейного программирования.

Двойственные задачи линейного программирования

Транспортная задача.

Составление инвестиционной программы


26 ≤ ????1 ≤ 41

{22 ≤ ????2 ≤ 35,333

.

8 ≤ ????3 ≤ +∞

36 ≤ ????4 ≤ +∞

Ответим на несколько дополнительных вопросов:

  1. Определить нормы заменяемости ресурсов в оптимальном плане.

  2. Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья II и III вида на 2 и 16 единиц.

  3. Определить целесообразность включения в план нового изделия ценой 5 руб., на изготовление которого расходуется по две единицы каждого вида сырья.

Решение:

  1. Т.к. дефицитными являются только первое и второе сырье, найдем норму заменяемости этих ресурсов. Составим соотношение ????1⁄????2 = 1,6/1,2 = 4/3, т.е. для максимизации общей прибыли (выручки) каждые дополнительные 3 единицы первого ресурса эквивалентны дополнительным 4 единицам второго ресурса: 3????1 = 4????2.

  2. Изменения каждого из ресурсов лежит в пределах допустимых соотношений для сохранения оптимального решения двойственной задачи, поэтому изменение суммарного дохода предприятия при изменении ресурсов рассчитывается по формуле:


????
Δ???? ∑???? ????* ⋅ Δ????????

.
????????????

Следовательно, значение целевой функции станет равно 98,4 ден. ед..

Для определения плана производства и проверки неизменности теневых оценок при совместном изменении ресурсов решим задачу, используя в качестве ограничений ????2 = 34 и ????3 = 26 (рис. 4):



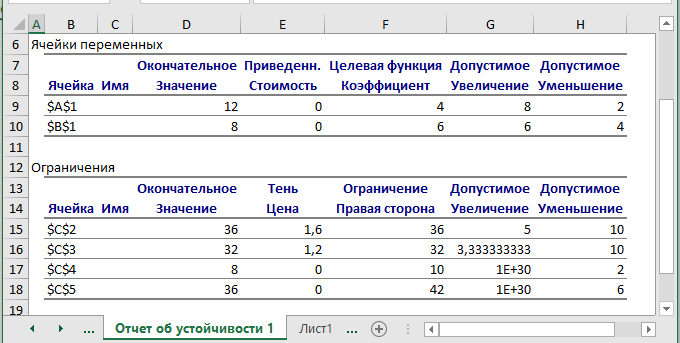
Рис. 4. Отчет по устойчивости при изменении ресурсов.
Таким образом, оптимальный план производства – 13,2 изделий I вида продукции и 7,6 изделий – II вида продукции, значение выручки при этом равно ???? = 4 ⋅ 13,2 + 6 ⋅ 7,6 = 98,4 ден. ед. Теневые цены при этом не изменились.

Ответы совпадают.

  1. Для определения целесообразности введения нового изделия воспользуемся соотношением:


????
∑ ????????????????* ≤ ????????

aij

????


i
y
* 21,6 21,200 5,6.

i

Производство нового вида продукции невыгодно, т.к. суммарные затраты на производство единицы продукции превосходят экономические выгоды при реализации: 5,6 5.

3. Двумерные задачи линейного программирования


  1. Закрытаятранспортнаязадача.

Пример.Пусть имеется:

  • Четыре пункта отправления: города с названием А1,А2,А3,А4,в которых сосредоточены запасы какого-либо товара (например, машин) соответственно в количестве; a1 350,a2 400,a3 250,a4 160

  • Пять пунктов назначения: города под названием В1, В2, В3,В4, В5, в которых сосредоточены потребители товара (машин), желающие получить его в количестве b1 250,b2 300,b3 200,b4 250,b5 160;

  • Установлено, что сумма заявок всех городов-потребителей товара равна суммарному количеству товара, имеющегося в городах-поставщиках этого товара, т.е.:

a1 a2 a3 a4 b b ;

  • Известна с

  • стоимость перевозки одной единицы товара (одной машины)

из пункта отправления A

перевозок:

в пункт назначения

Bj,т.е. задана матрица стоимостей

1 2



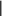
1 2 2



С c

2,5

2 1,5

1 1,5

.

ij 2



2

1,5

1

1,5

2

1,5

1,5

1,5



1,5

Экономическая постановка задачи: Требуется составить такой план перевозок, при котором весь имеющийся запас товара из всех городов-поставщиков, являющихся пунктами отправления был вывезен, все заявки городов-потребителей удовлетворены, а стоимость перевозок всего товара, который перевозится от поставщиков к потребителям, была бы минимальна. Условие задачи можно представить в виде таблицы:
b1=250
b2=300
b3=200
B4=250
B5=160

a1=350
1
2
1
2
2

a2=400
2,5
2
1,5
1
1,5

a3=250
2
1,5
1,5
1,5
1,5

a4=160
2
1
2
1,5
1,5

Математически эта задача формулируется следующим образом:

Обозначим через

xij–количество товара, который перевозится из пункта

отправления

Ai, в пункт назначения

Bj, (1 i 4,1

j 5).

Сформулируем для данной задачи систему ограничений:

  1. сумма товаров, содержащихся во всех пунктах отправления должна равняться сумме заявок на доставку этих товаров, которые подали все пункты назначения, т.е.:

4

ai

i1

5

bjj1

  1. все товары, имеющиеся в каждом из пунктов отправления, должны быть вывезены, возможно, в различные пункты назначения, т.е. должны выполняться равенства:

5

x1jj1

5

a1или

x11 x12 x х ,

x2 jj1

5

a2или

x21 x22 x23 х24 x25 a2,

x3j

5

или

x31 x32 x  ,

x4jj1

a4или

x41 x42 x43 х44 x45 a4,

  1. суммарное количество товара, доставляемого в каждый пункт назначения изо всех пунктов отправления, должно быть равно количеству заявок, поданных данным пунктом, т.е. должны выполняться равенства:

4

Смотрите также файлы