ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 103
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
задачи.
При наборе графика работы персонала учитывается пять рабочих дней и два выходных в неделю. Все рабочие графики вводятся в массив (B2:H8), причем «1» означает рабочий день графика, а «0» - выходной. Так первый график, представленный в столбце В, имеет два выходных в понедельник и вторник и 5 рабочих дней со среды по воскресенье. Массив (B1:H1) соответствует переменным задачи, т.е. количеству сотрудников работающих по определенному графику.
В ячейке I2 вводится формула СУММПРОИЗВ($B$1:$H$1;B2:H2), рассчитывающая количество сотрудников, работающих в понедельник (рис. 10). Аналогичные формулы вводятся и в ячейках I3:I9.
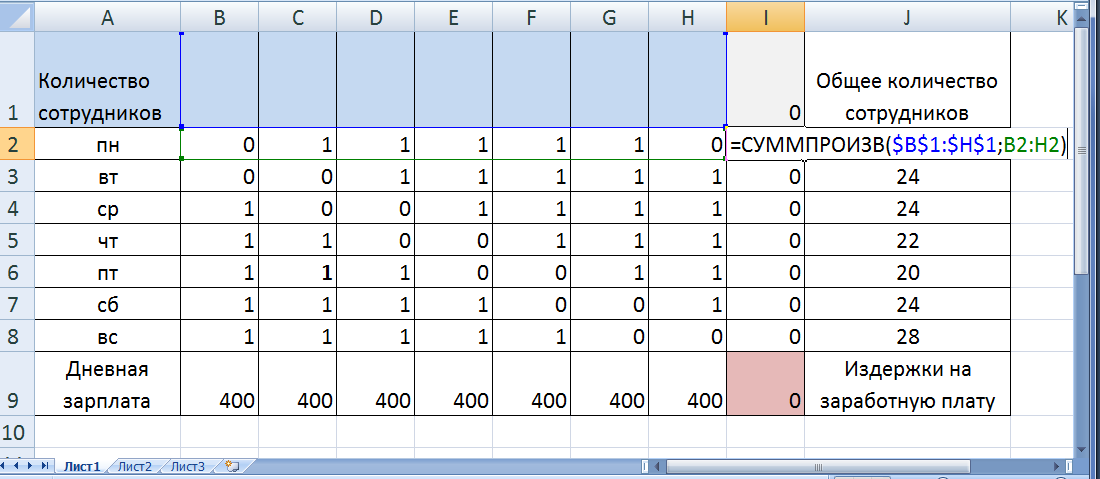
Рис. 10. Ввод левой части ограничений.
Для расчета общего количества сотрудников вводится формула СУММ(В1:Н1) в ячейку I1.
Граничные условия и ограничения вводят аналогично предшествующей задаче с помощью диалоговых окон Добавить в окне В соответствии с ограничениями. Целевую ячейку устремляют к минимуму. Метод решения – Поиск решения лин. задач симплекс-методом, установить флажок в поле Сделать переменные без ограничений неотрицательными (рис. 11).
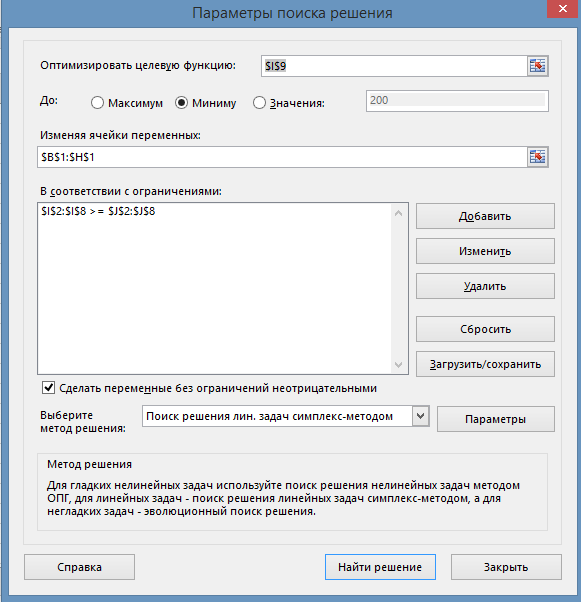
Рис. 11. Окно «Поиск решения» задачи.
Решение задачи представлено на рис. 12.

Рис. 12. Решение задачи.
В данном примере можно использовать ограничение целых чисел, если дробное число сотрудников недопустимо. Можно добавить ограничение на общее число сотрудников:
∑
????
????=1
???????? ≤ Х,
где Х– максимально допустимое число сотрудников фирмы.
Например, ограничение на целочисленность можно добавить с помощью окна ввода ограничений (рис. 13)
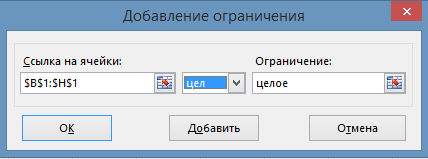
Рис. 13. Добавление ограничений на целочисленность.
Решение данной задачи показывает, что распределение сотрудников по рабочим графикам следующее:
13600 руб.
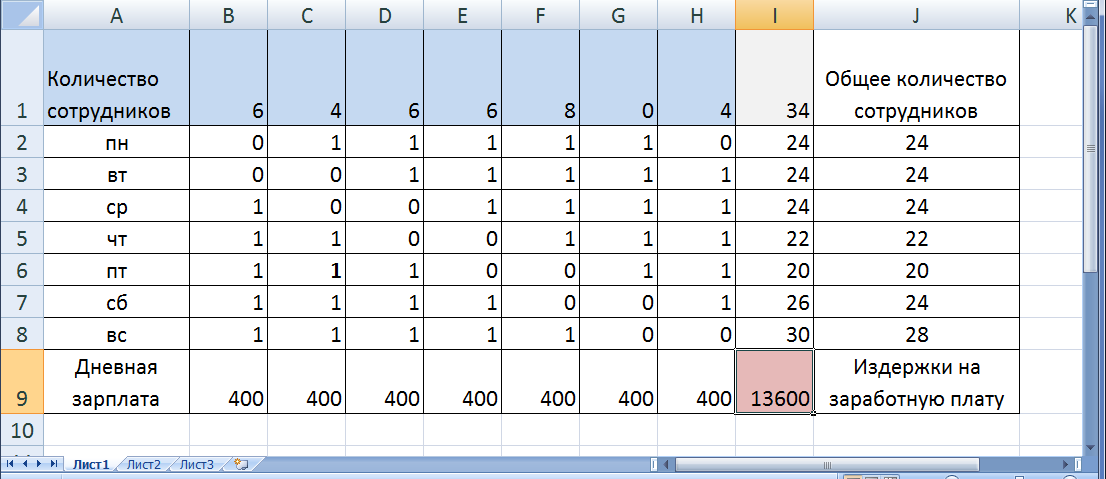
Рис. 14. Решение задачи с учётом целочисленности переменных.
Решение двойственной задачи можно найти, решая двойственную задачу линейного программирования или, решая прямую задачу линейного программирования, дополнительно потребовав в окне «Результаты поиска решения» два типа отчетов:
«Результаты»и «Устойчивость» (рис. 1), которые открываются на отдельных дополнительных листах книги Excel.
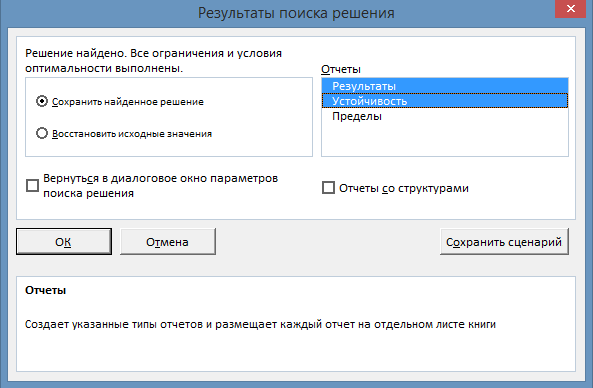
Рис. 1. Выделение типов отчетов для решения двойственной задачи.
Найдем двойственную задачу к прямой задаче, рассмотренной в п. 1.
Отчетпорезультатам. Отчет по результатам состоит из трех таблиц (рис. 2):
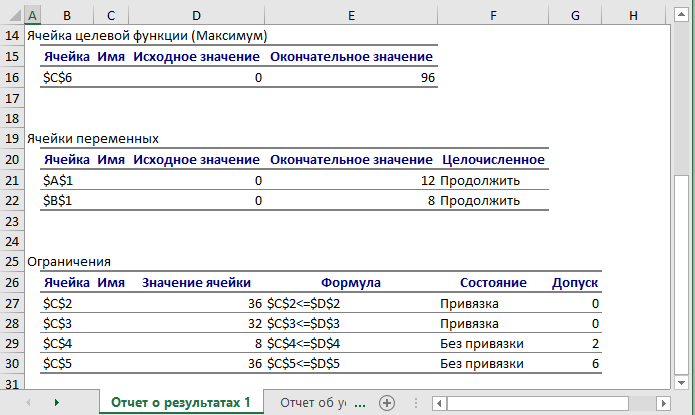
Рис. 2. Отчет по результатам
Если ресурс используется полностью, т.е. ресурс дефицитный, то в графе "Состояние" соответствующее ограничение указывается как "привязка"; при неполном использовании ресурса, т.е. ресурс недефицитный, в этой графе указывается
"без привязки".
В графе "Значение ячейки" приведены величины использованного ресурса. В графе "Допуск" показана разность между значением использованных ресурсов в найденном оптимальном решении и количеством ресурсов на складе, т.е. указано неиспользованное количество недефицитного сырья. Так, третьего ресурса использовано только 8 ед., неизрасходованным осталось 2 ед. сырья, которое осталось лежать на складе. Из этого следует, что запас недефицитного третьего ресурса можно уменьшить на 2 ед.и это никак не повлияет на оптимальное решение. Аналогично можно уменьшить на 6 ед. и четвертое недефицитное сырье.
Отчетпоустойчивости.Отчет по устойчивости состоит из двух таблиц (рис.
1. Приведённая стоимость, которая показывает, на сколько изменится значение целевой функции в случае принудительного включения единицы этой продукции в оптимальное решение. В нашем случае оба вида продукции входят в оптимальный план, поэтому нормированная стоимость нулевая.
{2 ≤ ????1 ≤ 12.
4 ≤ ????2 ≤ 14
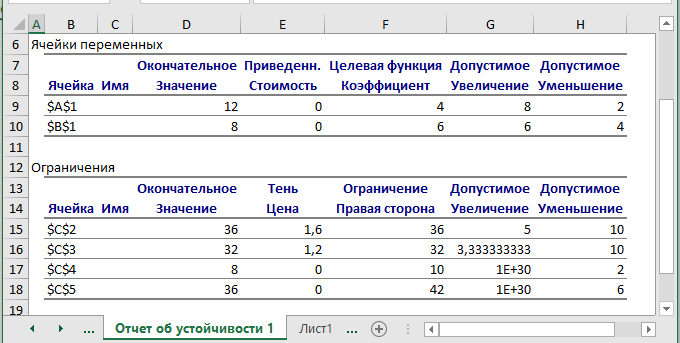
Рис. 3. Отчет по устойчивости.
Примечание.При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может меняться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры).
Таблица 2 (см. рис. 3) содержит информацию, относящуюся к ограничениям.
максимальную прибыль на 1,6 руб., а увеличение на единицу второго сырья – на 1,2 руб. Отсюда вывод: в первую очередь выгодно увеличивать количество первого ресурса.
При наборе графика работы персонала учитывается пять рабочих дней и два выходных в неделю. Все рабочие графики вводятся в массив (B2:H8), причем «1» означает рабочий день графика, а «0» - выходной. Так первый график, представленный в столбце В, имеет два выходных в понедельник и вторник и 5 рабочих дней со среды по воскресенье. Массив (B1:H1) соответствует переменным задачи, т.е. количеству сотрудников работающих по определенному графику.
В ячейке I2 вводится формула СУММПРОИЗВ($B$1:$H$1;B2:H2), рассчитывающая количество сотрудников, работающих в понедельник (рис. 10). Аналогичные формулы вводятся и в ячейках I3:I9.

Рис. 10. Ввод левой части ограничений.
Для расчета общего количества сотрудников вводится формула СУММ(В1:Н1) в ячейку I1.
Граничные условия и ограничения вводят аналогично предшествующей задаче с помощью диалоговых окон Добавить в окне В соответствии с ограничениями. Целевую ячейку устремляют к минимуму. Метод решения – Поиск решения лин. задач симплекс-методом, установить флажок в поле Сделать переменные без ограничений неотрицательными (рис. 11).

Рис. 11. Окно «Поиск решения» задачи.
Решение задачи представлено на рис. 12.

Рис. 12. Решение задачи.
В данном примере можно использовать ограничение целых чисел, если дробное число сотрудников недопустимо. Можно добавить ограничение на общее число сотрудников:
∑
????
????=1
???????? ≤ Х,
где Х– максимально допустимое число сотрудников фирмы.
Например, ограничение на целочисленность можно добавить с помощью окна ввода ограничений (рис. 13)

Рис. 13. Добавление ограничений на целочисленность.
Решение данной задачи показывает, что распределение сотрудников по рабочим графикам следующее:
-
по 6 сотрудников работают по рабочим графикам с выходными в понедельник-вторник, среда-четверг и четверг-пятница, -
по 4 сотрудника работают по графикам с выходными вторник-среда и воскресенье-понедельник, -
8 сотрудников имеют график работы с выходными в пятницу-субботу -
и график с выходными в субботу-воскресенье не имеет никто из сотрудников. Всего фирме требуется 34 сотрудника, еженедельные затраты на заработную плату
13600 руб.

Рис. 14. Решение задачи с учётом целочисленности переменных.
4. Двойственные задачи линейного программирования
Решение двойственной задачи можно найти, решая двойственную задачу линейного программирования или, решая прямую задачу линейного программирования, дополнительно потребовав в окне «Результаты поиска решения» два типа отчетов:
«Результаты»и «Устойчивость» (рис. 1), которые открываются на отдельных дополнительных листах книги Excel.

Рис. 1. Выделение типов отчетов для решения двойственной задачи.
Найдем двойственную задачу к прямой задаче, рассмотренной в п. 1.
Отчетпорезультатам. Отчет по результатам состоит из трех таблиц (рис. 2):
-
таблица 1 содержит информацию о целевой функции, в нашем случае оптимальное значение целевой функции равно 96 руб.; -
таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи: ???? = (12, 8); -
таблица 3 показывает результаты оптимального решения для ограничений и граничных условий.

Рис. 2. Отчет по результатам
Если ресурс используется полностью, т.е. ресурс дефицитный, то в графе "Состояние" соответствующее ограничение указывается как "привязка"; при неполном использовании ресурса, т.е. ресурс недефицитный, в этой графе указывается
"без привязки".
В графе "Значение ячейки" приведены величины использованного ресурса. В графе "Допуск" показана разность между значением использованных ресурсов в найденном оптимальном решении и количеством ресурсов на складе, т.е. указано неиспользованное количество недефицитного сырья. Так, третьего ресурса использовано только 8 ед., неизрасходованным осталось 2 ед. сырья, которое осталось лежать на складе. Из этого следует, что запас недефицитного третьего ресурса можно уменьшить на 2 ед.и это никак не повлияет на оптимальное решение. Аналогично можно уменьшить на 6 ед. и четвертое недефицитное сырье.
Отчетпоустойчивости.Отчет по устойчивости состоит из двух таблиц (рис.
-
Таблица 1 содержит информацию, относящуюся к переменным.-
Результатрешениязадачи: ???? = (12, 8).
-
1. Приведённая стоимость, которая показывает, на сколько изменится значение целевой функции в случае принудительного включения единицы этой продукции в оптимальное решение. В нашем случае оба вида продукции входят в оптимальный план, поэтому нормированная стоимость нулевая.
-
Коэффициенты целевойфункции???? = 4????1 + 6????2. -
ДопустимыезначенияприращенияцелевыхкоэффициентовΔ????????,при которых сохраняется первоначальное оптимальное решение прямой задачи. Например, допустимоеувеличение цены на первый товар составляет 8 руб./шт., а допустимое уменьшение – 2руб./шт. (строка 9 на рис. 3). Это означает, что если цена на первый товар возрастет более чем на 8 руб./шт., например, станет равной 14 руб./шт., то оптимальное решение изменится. Анализируя предельные изменения цены на товары, мы получаем, что оптимальное решение прямой задачи не изменится, если цена на продукцию не превысит заданных пределов:
{2 ≤ ????1 ≤ 12.
4 ≤ ????2 ≤ 14

Рис. 3. Отчет по устойчивости.
Примечание.При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может меняться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры).
Таблица 2 (см. рис. 3) содержит информацию, относящуюся к ограничениям.
-
Величинаиспользованныхресурсовв графе "Окончательное значение" и величина ресурсов на складе в графе "Ограничение правая сторона". Анализ двух граф иллюстрирует, что первый и второй ресурс использованы полностью, третий и четвертый ресурс – не полностью. -
Ценность дополнительной единицы i-го ресурса (теневая цена)– оптимальное решение двойственной задачи.????* = (1,6; 1,2; 0; 0). Следовательно, первый и второй ресурсы дефицитные, а третий и четвертый недефицитные. Первый ресурс является наиболее дефицитным, поэтому увеличение первого сырья на единицу увеличит
максимальную прибыль на 1,6 руб., а увеличение на единицу второго сырья – на 1,2 руб. Отсюда вывод: в первую очередь выгодно увеличивать количество первого ресурса.
-
ПредельныезначенияприращенияресурсовΔ????????. В графах «Допустимое Уменьшение» и «Допустимое Увеличение» показывается, на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом оптимальное решение двойственной задачи. Анализируя предельные изменения ресурсов, мы получаем, что оптимальное решение двойственной задачи не изменится, если изменение ресурсов не превысит заданных пределов:


