ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 114
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ссылку можно помощью клавиши F4.
На рис. 2 представлен общий вид листа Excel после ввода зависимостей математической модели.
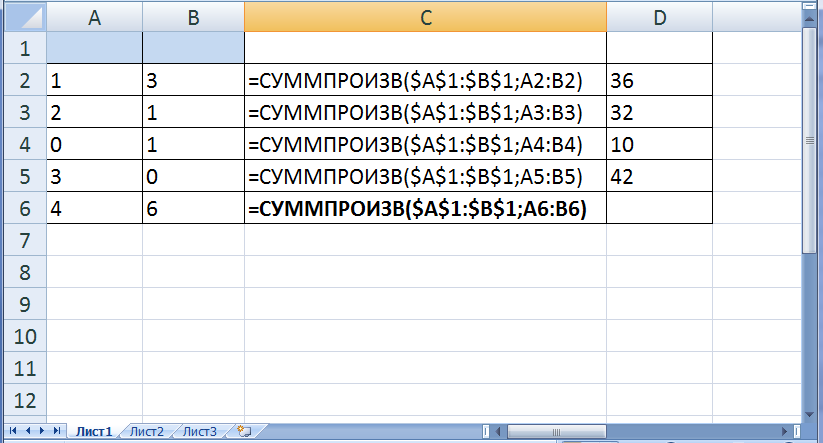
Рис. 2. Ввод системы ограничений.
Целевая функция в ячейке С6.
Для решения задачи воспользуемся макрофункцией «Поиск_решения»'>«Поиск решения», которое вызывается из меню «Данные» (рис. 3):
В поле «Изменяя ячейки переменных» впишите адрес матрицы Х: $А$1:$В$1. Необходимые адреса можно вносить в поле автоматически путем выделения мышью соответствующих ячеек переменных.
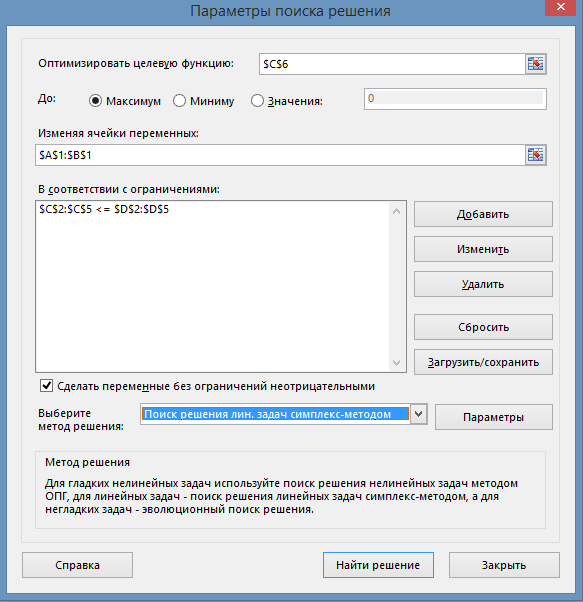
Рис. 3. Окно «Поиск решения».
Задание системы ограничений. Для введения системы ограничений необходимо в поле «В соответствии с ограничениями» открыть диалоговое окно «Добавить»(рис. 4):
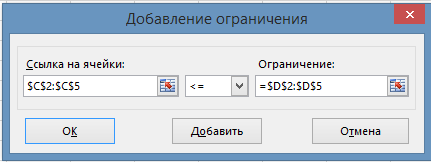
Рис. 4. Диалоговое окно Добавление ограничений.
$С$2, так как условие соотношения между правыми и левыми частями в нашей задаче одинаково, то в качестве ссылки на ячейку можно задать массив ($С$2:$С$5).
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 3).
Задание граничных условий для допустимых значений переменных. В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю. Ввести это ограничение можно путем установки флажка в окно Сделать переменные без ограничений неотрицательными (рис. 3).
3. Решение задачи
Установкаметодарешениязадачи.В поле «Выберите метод решения» необходимо выбрать симплекс-метод решения задач линейного программирования: «Поиск решения лин. задач симплекс-методом» (рис. 3).
Запуск задачи на решение производится путем нажатия кнопки «Найти решение».
После запуска на решение задачи линейного программирования появляется окно
«Результаты поиска решения» с одним из сообщений, представленных на рис. 5, 6 и 7:
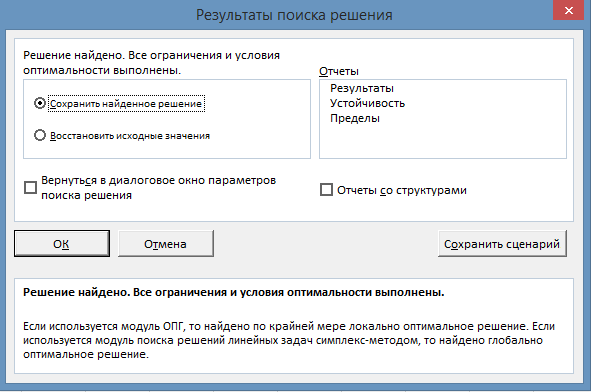
Рис. 5. Сообщение об успешном решении задачи.
Рис. 6. Сообщение при несовместной системе ограничений задачи.
 Рис. 7. Сообщение при неограниченности целевой функции в требуемом
Рис. 7. Сообщение при неограниченности целевой функции в требуемом
направлении.
Иногда сообщения, представленные на рис. 6 и 7, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий
задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение.
Если при заполнении полей макрофункции «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Точность ограничения» в вкладке «Параметры» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов:
«Результаты», «Устойчивость», «Пределы» (рис. 5). Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, целевой функции и левых частей ограничений) в окне нажмите кнопку «OK».
После этого появляется оптимальное решение задачи (рис. 8).
Таким образом, оптимальный план производства – 12 изделий I вида продукции и 8 изделий – II вида продукции, значение выручки при этом равно 96 ден. ед.
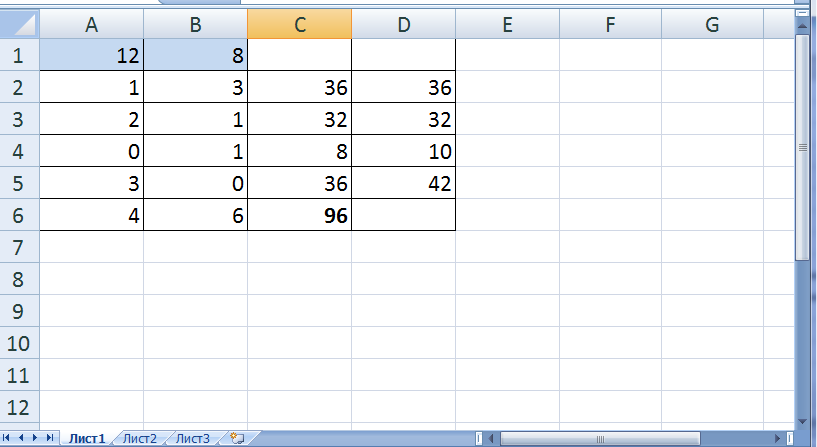
Рис. 8. Решение задачи
Пример2.Составлениеграфикаработыперсонала.
Для работы
в офисе компании по продаже недвижимости требуется в понедельник – среду – не менее 24 работника, в четверг и субботу - не менее 22 работников, в пятницу – не менее 20 работников, основной пик работы приходится в воскресенье, поэтому в воскресенье требуется не менее 28 сотрудников. Причем должен соблюдаться следующий рабочий график: каждый сотрудник работает 5 дней в неделю с 2-мя выходными подряд.
Дневная оплата сотрудников составляет 400 р. (без учета премиальных и комиссионных).
Определите оптимальное количество человек в смену для обслуживания офиса риэлтерской компании с учетом минимума издержек на заработную плату, учитывая установленный график работы персонала.
Решение:
1. Математическая модель: Пусть ???????? - число сотрудников, работающих по j-ому графику. Матрица графиков работы сотрудников А:

Матрица необходимого количества сотрудников на каждый рабочий день: ????Т= (24 24 24 22 20 22 28).
Матрица почасовой оплаты труда с = (400 400 400 400 400 400 400).
Система ограничений на обязательный минимум количества сотрудников в каждый рабочий день:
????2 + ????3 + ????4 + ????5 + ????6 ≥ 24 ﻟ????3 + ????4 + ????5 + ????6 + ????7 ≥ 24
I????1 + ????4 + ????5 + ????6 + ????7 ≥ 24
????1 + ????2 + ????5 + ????6 + ????7 ≥ 22
❪????1 + ????2 + ????3 + ????6 + ????7 ≥ 20
I????1 + ????2 + ????3 + ????4 + ????7 ≥ 22
 ????????1 + ????2 + ????3 + ????4 + ????5 ≥ 28
????????1 + ????2 + ????3 + ????4 + ????5 ≥ 28
И ограничение на неотрицательность переменных модели: ????????>0. Целевая функция
– минимум затрат на заработную плату:
???? = 400????1 + 400????2 + 400????3 + 400????4 + 400????5 + 400????6 + 400????7 → ????????????.
1. Ввод исходных данных:
Расширенная матрица задачи и вместе с введенными в нее необходимыми формулами, соответствующими левой части системы ограничений, представлена на рис.9.
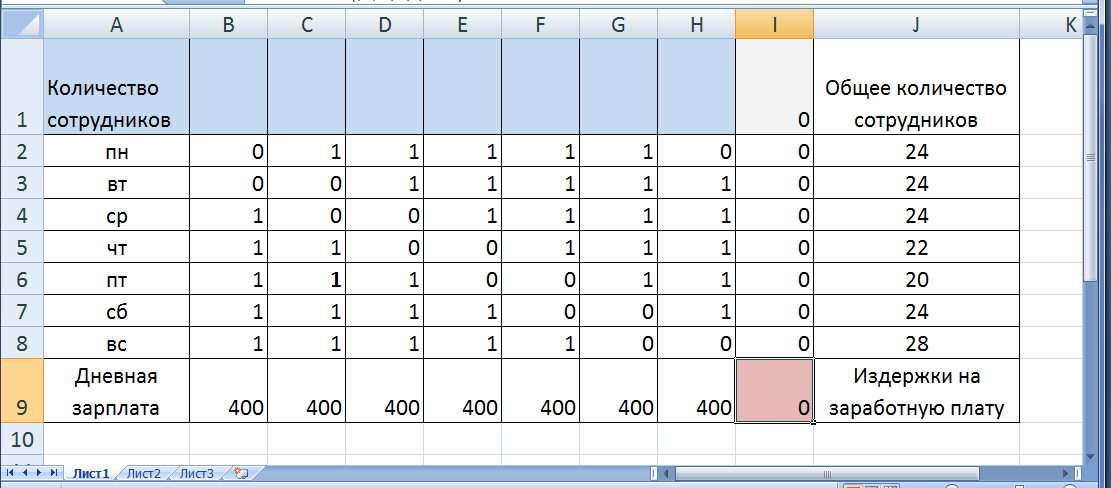
Рис. 9. Расширенная матрица
На рис. 2 представлен общий вид листа Excel после ввода зависимостей математической модели.

Рис. 2. Ввод системы ограничений.
Целевая функция в ячейке С6.
Для решения задачи воспользуемся макрофункцией «Поиск_решения»'>«Поиск решения», которое вызывается из меню «Данные» (рис. 3):
-
в поле «Установить целевую ячейку» введите адрес целевой ячейки $С$6; -
укажите, что целевая функция стримится к «максимальному значению».
В поле «Изменяя ячейки переменных» впишите адрес матрицы Х: $А$1:$В$1. Необходимые адреса можно вносить в поле автоматически путем выделения мышью соответствующих ячеек переменных.

Рис. 3. Окно «Поиск решения».
Задание системы ограничений. Для введения системы ограничений необходимо в поле «В соответствии с ограничениями» открыть диалоговое окно «Добавить»(рис. 4):

Рис. 4. Диалоговое окно Добавление ограничений.
-
В поле «Ссылка на ячейку» введите адреса ячеек левой части ограничений
$С$2, так как условие соотношения между правыми и левыми частями в нашей задаче одинаково, то в качестве ссылки на ячейку можно задать массив ($С$2:$С$5).
-
В поле знака откройте список предлагаемых знаков и выберите ≤. -
В поле «Ограничение» введите адреса ячеек правой части ограничений, то есть $D$2:$D$5. Их также можно ввести путем выделения мышью непосредственно в таблице Excel.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 3).
Задание граничных условий для допустимых значений переменных. В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю. Ввести это ограничение можно путем установки флажка в окно Сделать переменные без ограничений неотрицательными (рис. 3).
3. Решение задачи
Установкаметодарешениязадачи.В поле «Выберите метод решения» необходимо выбрать симплекс-метод решения задач линейного программирования: «Поиск решения лин. задач симплекс-методом» (рис. 3).
Запуск задачи на решение производится путем нажатия кнопки «Найти решение».
После запуска на решение задачи линейного программирования появляется окно
«Результаты поиска решения» с одним из сообщений, представленных на рис. 5, 6 и 7:

Рис. 5. Сообщение об успешном решении задачи.

Рис. 6. Сообщение при несовместной системе ограничений задачи.
 Рис. 7. Сообщение при неограниченности целевой функции в требуемом
Рис. 7. Сообщение при неограниченности целевой функции в требуемомнаправлении.
Иногда сообщения, представленные на рис. 6 и 7, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий
задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение.
Если при заполнении полей макрофункции «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Точность ограничения» в вкладке «Параметры» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов:
«Результаты», «Устойчивость», «Пределы» (рис. 5). Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, целевой функции и левых частей ограничений) в окне нажмите кнопку «OK».
После этого появляется оптимальное решение задачи (рис. 8).
Таким образом, оптимальный план производства – 12 изделий I вида продукции и 8 изделий – II вида продукции, значение выручки при этом равно 96 ден. ед.

Рис. 8. Решение задачи
Пример2.Составлениеграфикаработыперсонала.
Для работы
в офисе компании по продаже недвижимости требуется в понедельник – среду – не менее 24 работника, в четверг и субботу - не менее 22 работников, в пятницу – не менее 20 работников, основной пик работы приходится в воскресенье, поэтому в воскресенье требуется не менее 28 сотрудников. Причем должен соблюдаться следующий рабочий график: каждый сотрудник работает 5 дней в неделю с 2-мя выходными подряд.
Дневная оплата сотрудников составляет 400 р. (без учета премиальных и комиссионных).
Определите оптимальное количество человек в смену для обслуживания офиса риэлтерской компании с учетом минимума издержек на заработную плату, учитывая установленный график работы персонала.
Решение:
1. Математическая модель: Пусть ???????? - число сотрудников, работающих по j-ому графику. Матрица графиков работы сотрудников А:

| 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| l1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| I1 | 1 | 1 | 0 | 0 | 1 | 1I |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| ????1 | 1 | 1 | 1 | 1 | 0 | 0) |
Матрица необходимого количества сотрудников на каждый рабочий день: ????Т= (24 24 24 22 20 22 28).
Матрица почасовой оплаты труда с = (400 400 400 400 400 400 400).
Система ограничений на обязательный минимум количества сотрудников в каждый рабочий день:
????2 + ????3 + ????4 + ????5 + ????6 ≥ 24 ﻟ????3 + ????4 + ????5 + ????6 + ????7 ≥ 24
I????1 + ????4 + ????5 + ????6 + ????7 ≥ 24
????1 + ????2 + ????5 + ????6 + ????7 ≥ 22
❪????1 + ????2 + ????3 + ????6 + ????7 ≥ 20
I????1 + ????2 + ????3 + ????4 + ????7 ≥ 22
 ????????1 + ????2 + ????3 + ????4 + ????5 ≥ 28
????????1 + ????2 + ????3 + ????4 + ????5 ≥ 28И ограничение на неотрицательность переменных модели: ????????>0. Целевая функция
– минимум затрат на заработную плату:
???? = 400????1 + 400????2 + 400????3 + 400????4 + 400????5 + 400????6 + 400????7 → ????????????.
1. Ввод исходных данных:
Расширенная матрица задачи и вместе с введенными в нее необходимыми формулами, соответствующими левой части системы ограничений, представлена на рис.9.

Рис. 9. Расширенная матрица


