Файл: Варианты контрольной работы.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.05.2024

Просмотров: 133

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Варианты контрольной работы

Примеры решения задач

2. Регрессионный анализ. Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных X j(j=1,2,...k), рассматриваемых в регрессионном анализе как kнеслучайных величин, независимо от истинного закона распределения Xj . YОбычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием  (X1,X2 ,...,Xk), являющимся функцией от аргументов Xj, и постоянной, не зависящей от аргументов дисперсией 2 . Пусть из генеральной совокупности (Y,X1 ,X2 ,...,Xk)берется выборка Yобъемом n(yi,x1i,x2i,...,xkn)i 1,k. Требуется по выборке найти оценку уравнений регрессии  (X1,X2 ,...,Xk)и исследовать его свойства. Вид функции выбирают заранее, наиболее часто встречающиеся: Y Линейная  0 1X1 2 X2 ...kXk; Полиномиальная     X  X2 ... Xk; Y 0 1 2 k Степенная (логарифмически-линейная)    X1  X2 ...XK Y 0 1 2 k Линейная двумерная модель. Необходимо найти оценку двумерного линейного уравнения регрессии:Y 0  1X y b0  b1x ei. (1)Для оценки неизвестных параметров 0 и 1 из двумерной генеральной совокупности (X,Y)берется выборка объемом n, где ( yi,xi) результат i-того наблюдения ( i 1,2,...,n). Оценку 0 и 1 производится с помощью метода наименьших квадратов (МНК).Согласно МНК, в качестве оценок неизвестных параметров 0 и 1 следует братьтакие значения выборочных характеристик b0 и b1 , которые минимизируют сумму квадратов отклонений: nQ (y b bx)2  min.  i 0 1 i  i1 0 1Исследуя функцию Qна минимум, получим:  Q 0 Q 2(y b bx) 0 b bi 0 1 i b0n b1 xi  yi   0  0  2(2)  Q 0Q 2(y b bx)x 0 b0  xi b1 xi  yixi bbi 0 1 i i  1  1 i i i i;Решая эту систему уравнений, например, методом Крамера получаем: b0  yi x2   x xyb1 nxiyixiyi(3) i i i in x2  ( x)2 n x2  ( x)2 ????Оценка ????2 остаточной дисперсии 2 имеет вид: ????2 = 1∑????(????− ????− ???? ???? )2(4) ???? ????−2????=1 ????0 1 ???? Проверказначимостиинахождениеинтервальныхоценоккоэффициентоврегрессии Для проверки соответствия уравнения регрессии экспериментальным данным. В MS Excel для этих целей рассчитывается Значимость F. Если Значимость F < α. принятого в задаче, то модель соответствует экспериментальным данным. Для проверки значимости коэффициентов регрессии В MS Excel для этих целей рассчитывается P-значение. Если Р-значение < α. принятого в задаче, то коэффициент регрессии значим.Если значим коэффициент регрессии b1, то значимо и уравнение регрессии. Линейная множественная модель. Рассмотрим общий случай линейной регрессии, когда условное математическое Y ожидание есть функция kпеременных: Y 0 1X1 2 X2 ...kXk. В матричном виде это уравнение примет вид: Y X , где Y- вектор-столбец наблюденийразмерности ( n  1); X- матрица факторных признаков размерности ( n  ( k  1));  - вектор неизвестных параметров размерности ((k 1) 1).Оценка МНК вектора  имеет вид:b XT X1 XT Y, где XT- транспонированная матрица Х, XT X1 - матрица, обратная матрице XT X.Несмещенная оценка остаточной дисперсии: ????2 = 1(???? − ????????)????(???? − ????????), ???? ????−????−1ПримеррешениязадачилинейнойдвумернойрегрессииНа основании выборочных данных по 20 туристическим фирмам о затратах на рекламу (Х) и количества туристов, воспользовавшихся услугами фирмы (Y), представленных в таблице, вычислить статистические характеристики двумерной линейной регрессионной модели. Определите соответствие модели экспериментальным данным и значимость регрессионной модели. Определите доверительные интервалы коэффициентов регрессии. Уровень значимости равен 5%. X 8,1 8,2 8,6 9,2 9,4 9,5 9,8 9,9 10,1 10,3 Y 800 850 720 850 800 880 950 820 900 1000 X 10,4 10,5 10,6 11,2 11,3 11,7 11,9 12,4 12,5 12,7 Y 920 1060 950 900 1200 1150 1000 1200 1100 1000 Решение:Построение уравнения линейной регрессии. Для построения линейной регрессии воспользуемся макрофункцией Регрессия (рис. 1). Для макрофункции Регрессия важно, чтобы группирование переменных было по столбцам.Входные интервалы переменных Х и Y вводим вместе с названиями и ставим флажок в поле Метки, чтобы показать, что в первой строке стоят названия переменных. Отмечаем выходной интервал и ставим флажок в графике подбора, на котором отображается корреляционное поле, включающее экспериментальные данные и регрессионную модель. Рис. 1. Макрофункция Регрессия.Выходной интервал содержит 3 таблицы (рис. 2). В первой таблице отражается коэффициент корреляции ρ, коэффициент детерминации R2, нормированный коэффициент детерминации ????2 и стандартная ошибка ???? .норм ???? Рис. 2. Нахождение линейной регрессии.Во второй таблице проводится анализ соответствия модели экспериментальным данным. В третьей таблице представлена информация о коэффициентах регрессии, их значимости и доверительных интервалах.Выводы: норм????2 <0.7 связь между переменными слабая.  ????е=85,07. Значимость F< 0,05, следовательно, модель соответствует экспериментальным данным. Р-значение для коэффициента b0 больше α=0,05, следовательно, коэффициент незначим. Р-значение для коэффициента b1 меньше α=0,05, следовательно, коэффициент значим. Значимость коэффициента b1 свидетельствует о значимости регрессионной модели. Уравнение регрессии имеет вид: ????̃ = 139,29 + 78,08????  Доверительные интервалы ????0 ∈ [−171,54; 450,11] и ????1 ∈ [48,48; 107,68]Примеррешениязадачимножественной линейнойрегрессии.В таблице приведены результаты работы 27 предприятий:

3. Задачи линейного программирования.

4. Двойственные задачи линейного программирования

3. Двумерные задачи линейного программирования

Инвестиционный анализ. Сравнение инвестиционных проектов

Практические задания

Регрессионный анализ

Задачи линейного программирования.

Двойственные задачи линейного программирования

Транспортная задача.

Составление инвестиционной программы





Х1
140
180
160
170
175
150
140
143
150
135
160
120
120
150

Х2
129
125
120
126
136
104
116
112
109
113
113
104
103
125

Y
80
99
86
92
95
82
76
80
85
75
87
69
65
84

Зависимой переменной Y является чистая прибыль, независимые переменные – авансированный капитал – X1 и собственный капитал – X2 . Требуется:

  1. Определить оценки коэффициентов линейного уравнения регрессии

Y X Xи оценку остаточной дисперсии S2 ; проверить при =0,04

0 1 1 3 2 ост

соответствие модели экспериментальным данным и значимость уравнения регрессии.

Решение: Построение линейной множественной модели. Для построения модели используем макрофункцию Регрессия (рис. 3).



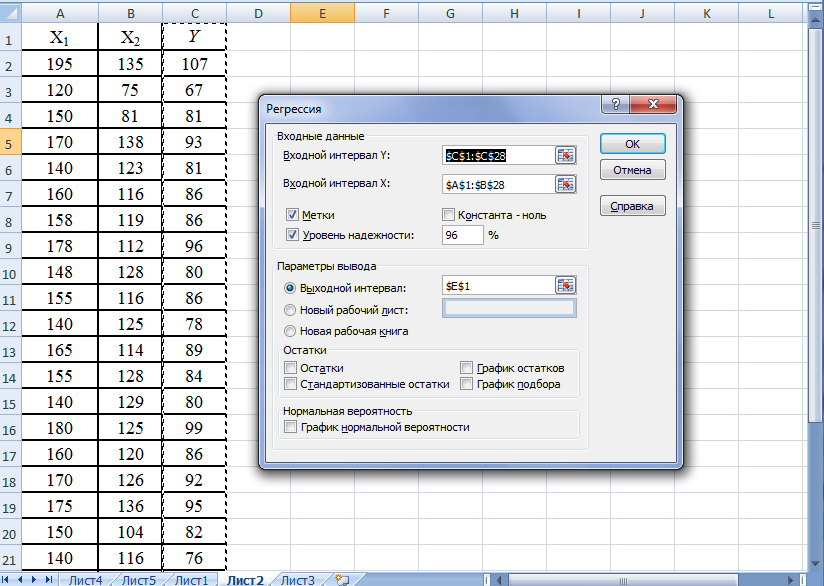
Рис. 3. Макрофункция Регрессия.
Входной интервал для переменной Х включает два столбца Х1 и
Х2. Уровень надежности определяется равным 96%, т.к уровень значимости α=5%.



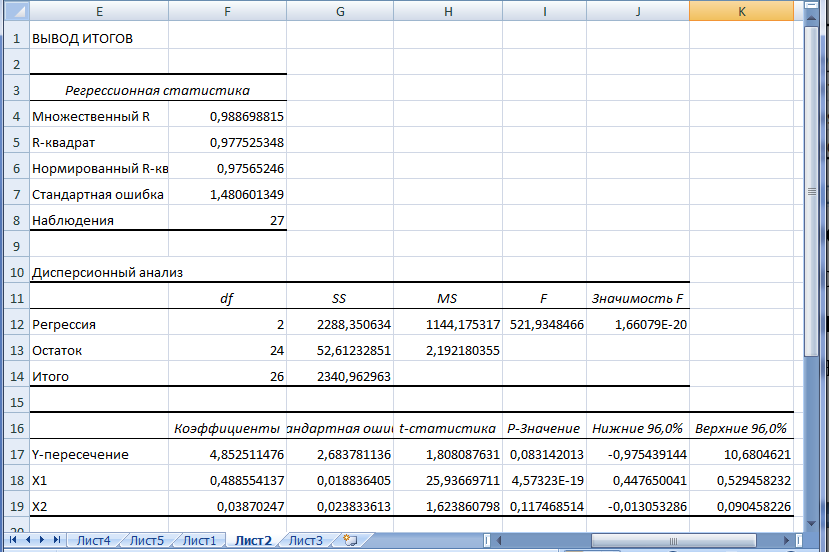
Рис. 4. Нахождение множественной линейной регрессии.
Анализ данных множественной линейной регрессии показывает (рис. 4), что 97,6% вариации Y объясняется влиянием переменных, входящих в модель. Модель соответствует экспериментальным данным, т.к. «Значимость F»=1,66 ⋅ 10−20, что меньше 0,04. Но модель незначима, т.к. коэффициент регрессии при переменной Х2 незначим (Р-значение=0,117 > 0,04).

Выводы:


  • норм
    ????2 >0,9 связь между переменными сильная.

????????=1,53.

  • Значимость F<0,05, следовательно, модель соответствует экспериментальным данным.

  • Р-значение для коэффициента b0 больше α=0,04, следовательно, коэффициент незначим.

  • Р-значение для коэффициента b1 меньше α=0,05, следовательно, коэффициент значим.

  • Р-значение для коэффициента b2 больше α=0,05, следовательно, коэффициент незначим.

  • Но модель незначима, т.к. коэффициент регрессии при переменной Х2 незначим

  • Уравнение регрессии имеет вид: ????̃ = 6,76 + 0,51х1



3. Задачи линейного программирования.


Для решения задач линейного программирования (ЛП) воспользуемся офисным приложением Microsoft Excel.

Эффективным средством решения задач линейного и нелинейного программирования в ППП Excel является макрофункция «Поиск решения». Эта макрофункция способна работать с достаточно сложными моделями оптимизации, в которых можно задавать несколько ограничений и изменяемых параметров. В процедуре

«Поиска решения» Excel используется алгоритм нелинейной оптимизации – нелинейный метод обобщенного понижающего градиента для гладких нелинейных задач, алгоритмы симплексного метода и метода «branch-and-bound» для решения линейных и целочисленных задач с ограничениями, а также эволюционный метод для решения негладких задач программирования.

Для того чтобы решить задачу линейного программирования в Excel, необходимо выполнить следующие действия.

    1. Формализоватьзадачу:

а) определить переменные модели; б) написать систему ограничений; в) задать целевую функцию.

    1. ВвестиусловиезадачивExcel:

a) ввести расширенную матрицу задачи:

    • коэффициенты при переменных в ограничениях,

    • правые части ограничений;

    • коэффициенты целевой функции,

б) ввести зависимости из математической модели на лист Excel:

    • формулу для расчета целевой функции,

    • формулы для расчета значений левых частей ограничений;

в) задать целевую функцию в окне «Поиск решения» и направление оптимизации:
минимум или максимум;

г) в поле «Изменяя значения переменных» ввести ячейки со значениями переменных;

д) ввести ограничения и граничные условия в поле «В соответствии с ограничениями»:

    • граничные условия для допустимых значений переменных,

    • соотношения между правыми и левыми частями ограничений.

    1. Решитьзадачу:

a) установить метод решения задачи в поле «Выберите метод решения»

б) запустить задачу на решение с помощью пиктограммы «Найти решение» и выполнить одно из указанных действий:

  • для сохранения решения на листе выберите вариант Сохранить найденной решение;

  • для восстановления исходных значений выберите вариант Восстановить исходные значения;

  • для создания отчётов о найденном решении выберите тип отчёта в поле

Отчёты и нажмите Ок;

  • для сохранения значения ячейки переменной в качестве сценария, который можно будет отобразить позже нажмите кнопку Сохранить сценарий и введите название сценария.

Пример1.Задачаобоптимальномиспользованииресурсов:

Решим задачу: для изготовления двух видов продукции используются четыре вида ресурсов. Максимально возможные запасы ресурсов различных видов, а также затраты на изготовление единицы каждого из двух видов продукции приведены в таблице.


Вид ресурса

Запас ресурса
Число единиц ресурсов, затрачиваемых на изготовление единицы продукции

Первый вид продукции
Второй вид продукции

В1
36
1
3

В2
32
2
1

В3
10
-
1

В4
42
3
-

Определить оптимальный план производства продукции, при котором затраты на производство продукции были бы в пределах возможного максимального ресурсного обеспечения, а выручка фирмы – наибольшей, если цена единицы продукции I вида – 4 ден. ед., а II вида – 6 ден. ед.

Решение: 1. Математическая модель:

х???? - план производства продукции j-того вида. Система ограничений на использование ресурсов:

????1 + 3????2 ≤ 36,

2????1 + ????2 ≤ 32,

{ ????2 ≤ 10,

3????1 ≤ 42.

Граничные условия:????1 ≥ 0, ????2 ≥ 0,

Целевая функция: ???? = 4????1 + 6????2 → ????????????.

Ввод исходных данных. Для решения задачи, введём расширенную матрицу задачи на листе Excel (рис.1). На рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel:

  • Матрица переменных Х= (х1, х2) соответствует ячейкам (А1:В1).

  • Технологическая матрица А= ‖????????????‖ соответствует массиву (А2:В5).

  • Правым частям ограничений ???? = ‖????????‖соответствуют ячейки (D2:D5).

  • Значениям целевой функции – ячейки (А6:В6).



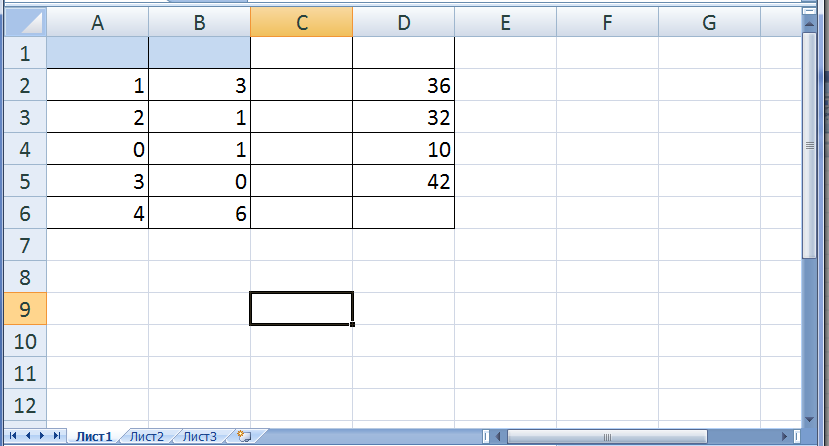
Рис. 1. Расширенная матрица задачи.

Для ввода системы ограничений используем формулу СУММПРОИЗВ(массив1; массив 2). Данная формула вводится в ячейки (С2:С6). Символ $ перед номером строки 1 означает абсолютную ссылку на переменные матрицы Х, следовательно, при копировании этой формулы в другие места листа Excel номер строки 1 не изменится. Абсолютную

Смотрите также файлы