ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 113
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6. Теория игр
1.Стратегическиеигры.Две конкурирующих фирмы, выпускающие стиральные машины, имеют следующие доли общего сбыта своей продукции на местном рынке; 53% –
фирма 1 и 47% – фирма 1. Обе фирмы пытаются увеличить объем своих продаж. Для этого
у них есть следующие альтернативы:
А1(В1)– расширить сеть сбыта;
А2(В –
рекламировать свою продукцию;
А3(В3)– увеличить ассортимент (число моделей
стиральных машин).Анализ показал, что при осуществлении обеими фирмами указанных мероприятий доля (в %) фирмы 1 на рынке стиральных машин изменится следующим образом:| Стратегия фирмы 1 Стратегия фирмы 2 | А1 | А2 | А3 |
| В1 | -4 | -5 | -1 |
| В2 | -1 | 0 | -3 |
| В3 | -3 | 1 | -5 |
Вопросы:1. Какое из мероприятий фирмы 1 наиболее эффективно?
1. Какую долю на рынке будет иметь фирма 1?
-
Какое из мероприятий фирмы 2 наиболее эффективно? -
С какой частотой фирме 2 следует использовать стратегию «реклама»?
Решение:Преобразуем платежную матрицу, увеличив все элементы матрицы на 6:
2 1 5
Q 5 6 3
3
1
7
Приведем матричную игру к задаче линейного программирования:
2y1 5y2 3y3 1
y 6y 7y 1
1 2 3
5y1 3y2 y3 1
yi 0
Z y1 y2 y3 min.
Для решения воспользуемся средствами Excel. На лист Excel внесём расширенную матрицу задачи и необходимые формулы для целевой функции и левых частей системы ограничений. Решим данную задачу с помощью макрофункции MS Excel «Поиск решения» (рис. 1).Выбираем симплекс-метод решения задач линейного программирования и неотрицательность переменных.
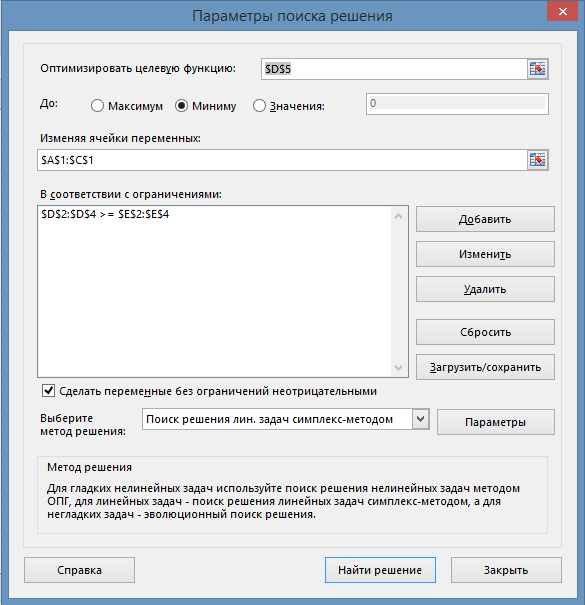
Рис. 1. Окно «Поиск решения».
После запуска в Excel задачи на решение в окне "Результаты поиска решения"
необходимо выделить с помощью мыши тип отчета: «Устойчивость».
В результате мы получаем решение и прямой и двойственной задачи (рис. 2 и 3).
Рис. 2. Решение задачи
В отчете по устойчивости показано решение двойственной задачи, относящейся к игроку В:
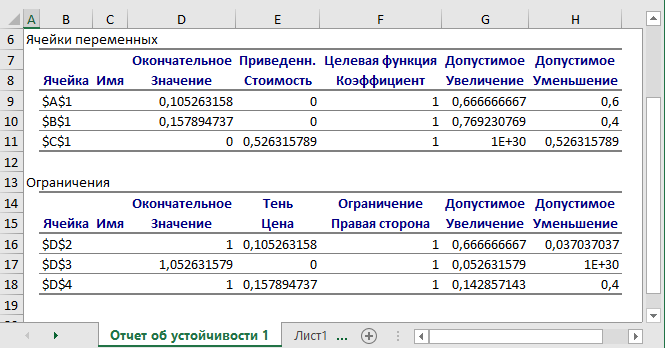
Рис. 3. Отчет по устойчивости.
Анализируя данные результаты, можно сделать следующие выводы:
-
Решение прямой задачи равно Y (0,105263;0,157895;0), целевая функция
равна 0,2631579, Следовательно, исправленная цена игры равна *
1
0,2631579
3,8.
Решением игры в смешанных стратегиях для игрока Аявляется следующий вектор,
определенный из условия
q
xj :
A1 A2
A3
A1
A2 A3
0,105263 3,8
0,157895 3,8
0 0,4
0,6 0
-
Решением двойственной задачи относительно игрока В является
Х (0,105263;0;0,157895), тогда решением игры в смешанных стратегиях для
игрока Вявляется следующий вектор:
| | B1 | B2 | B3 | В1 | В2 | В3 |
| 0,1 | 05263 3 | ,8 0 0 | ,157895 3,8 0,4 | 0 | 0,6 | |
-
Ответить на поставленные вопросы можно следующим образом:
-
для фирмы Анаиболее эффективной стратегией будет стратегия «Реклама»
(р2=0,6);
-
доля рынка фирмы Аснизится на 2,2%( 3,8 6 2,2(%)) и составит 53%- 2,2%=50,8%; -
для фирмы Внаиболее эффективной стратегией будет стратегия третья
«Расширение ассортимента» (q3=0,6);
-
вторую стратегию «Реклама» фирме Виспользовать не следует.
2.Статистическиеигры.Известна матрица доходов:
15 10 0
6 17
3 14 8 9 2
1 5 14 20 3
7 19 10 2 0
Используя методы принятия решений в условиях полной неопределенности, выберите оптимальную стратегию.
В предположении, что известны вероятности состояний природы, заданные вектором:
1
ПP
0,2
П20,1
П30,4
П40,2
П
5
,
0,1
выберите оптимальную стратегию, используя методы принятия решений в условиях частичной неопределенности.
Решение:Для выбора оптимальной стратегии в условиях полной неопределенности воспользуемся правилами Вальда, Сэвиджа и Гурвица.
-
ПравилоВальда.Используя функции МАКС и МИН выполним решение задачи в MSExcel:
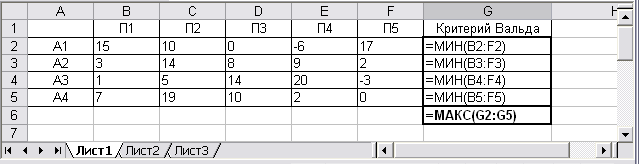
Рис. 4. Формулы для решения методом Вальда.
Рис. 5. Решение задачи методом Вальда
Получаем
maxminqij max 6
;2;3
;0 2,следовательно, согласно
i j i
критерию Вальда выбираем вторую стратегию А2, которая имеет максимальную гарантированную доходность.
-
ПравилоГурвица.Психологический параметр выберем равным 0,3. Используя
функции МАКС и МИН выполним решение задачи (6).
Рис. 6. Формулы для решения задачи методом Гурвица.
Рис. 7. Решение задачи методомГурвица.
Получаем minqij
j
6
;2;3;0
и maxqijj
17
;14
;20
;19
. Тогда
имеем:
max{0,3minqij (1 0,3)maxmaxqij}
i j i j
max{0,3 6
i
;2;3
;0 0,7 17
;14
;20
;19
max{10,1
i
;10,4
;13,1
;13,3} 13,3,
следовательно, согласно нашим психологическим склонностям выбираем четвертую
j
стратегию
А4 .
-
Правило Сэвиджа.Построим матрицу риска R
rij
, где rij= Вmax- Вij.
Рис. 8. Формулы для нахождения матрицы риска.
Рис. 9. Матрица риска.
Тогда используя формулы МАКС и МИН, найдем решение по критерию Сэвиджа:
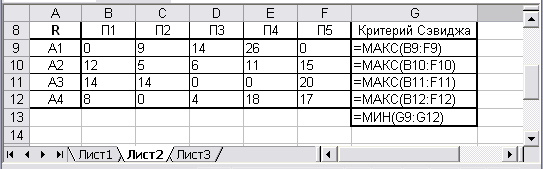
Рис. 10. Формулы для решения задачи методом Сэвиджа.
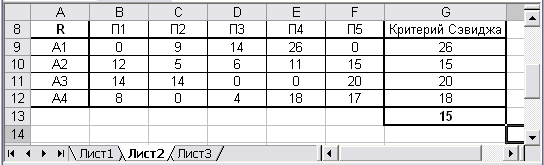
Рис. 11. Решение задачи методом Сэвиджа.
Следовательно, согласно критерия Сэвиджа
minmaxrij min26;15;20;18
15,
i j i
вторая стратегия
А2 имеет минимально возможный риск.
-
Критерий, основанный на известных вероятностных состояниях
«природы».Определим математические ожидания риска и доходности с помощью заданных
вероятностей и найдем максимум
M(B
и минимум M(R .
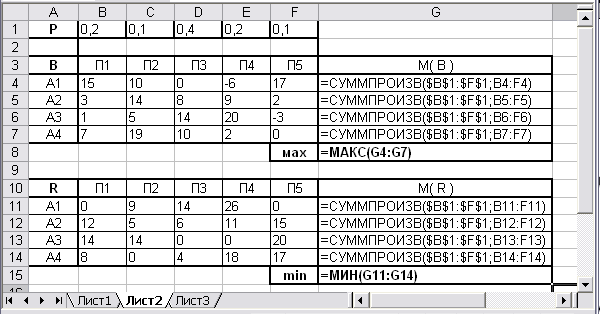
Рис. 12. Формулы для решения задачи в условиях риска.
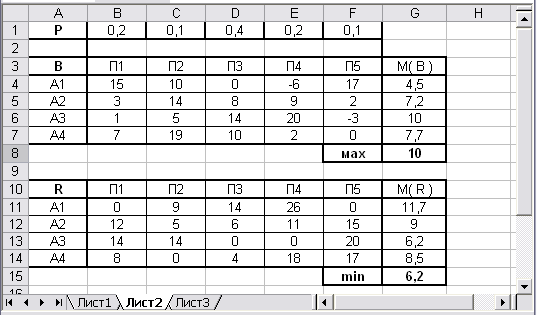
Рис. 13.
