Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 62
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
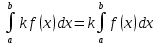
Свойство 4. Для несобственных интегралов 2-го рода справедлива формула интегрирования по частям
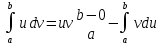
Свойство 5.Для несобственных интегралов 2-го рода справедлива формула замены переменной
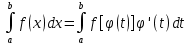
Следует заметить, что не все свойства определенного интеграла Римана переносятся на несобственные интегралы. Так например, произведение 2 интегрируемых, по Риману, на некотором отрезке функций является функцией так же интегрируемой, по Риману, на этом отрезке. Аналог этого утверждения для несобственных интегралов несправедлив.
-
Опишите способы вычисления площади фигуры с помощью определенного интеграла в декартовых координатах. Приведите примеры.
1. Задача о площади криволинейной трапеции
Определение 1. Фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a; b] функции y = f (x), осью Ох и прямыми х = а и х = b, называется криволинейной трапецией.
2) Если криволинейная трапеция примыкает к оси Oy, т. е. ограничена непрерывной кривой
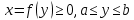 , 2 горизонтальными отрезками прямых y=a y=b и отрезком оси Oy квадрирема и ее площадь S равна.
, 2 горизонтальными отрезками прямых y=a y=b и отрезком оси Oy квадрирема и ее площадь S равна.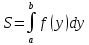
-
Если функция f(x) непрерывна на отрезке [a,b] и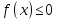 т.е. кривая y=f(x) и криволинейная трапеция, ограниченная снизу этой кривой, лежит под осью Ox то для вычисления ее площади следует рассмотреть функцию y=-f(x). Эта функция уже не отрицательна и следовательно ее график лежит над осью Ox и симметричен графику функцию y=f(x) относительно оси Ox,а криволинейная трапеция ограничена сверху y=-f(x) представляет собой зеркальное отражение первоначальной трапеции.
т.е. кривая y=f(x) и криволинейная трапеция, ограниченная снизу этой кривой, лежит под осью Ox то для вычисления ее площади следует рассмотреть функцию y=-f(x). Эта функция уже не отрицательна и следовательно ее график лежит над осью Ox и симметричен графику функцию y=f(x) относительно оси Ox,а криволинейная трапеция ограничена сверху y=-f(x) представляет собой зеркальное отражение первоначальной трапеции.
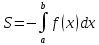
-
Некоторые части кривой y=f(x) находятся над осью Ox а другие под осью Ox. В этом случае площадь фигуры S представляет собой алгебраическую сумму тех частей фигуры, которые расположены над осью Ox и тех частей которые находятся под осью Ox, причем первые входят со знаком плюс а вторые со знаком минус.
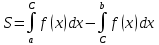
-
Пусть фигура ограничена снизу и сверху кривыми
Y1=f1(x) y2=f2(x)
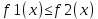
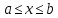
f1(x) f2(x) – непрерывные функции.
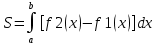
-
Опишите способ вычисления объема тела вращения с помощью определенного интеграла в декартовых координатах. Приведите пример.
Объём тела вращения в декартовых координатах
В случае, когда тело получено вращением некоторой кривой y=f(x) вокруг оси Ох (рис.20), в сечении этого тела плоскостями, перпендикулярными к оси Ох, будут получаться круги площади S(x)=πy2=πf 2(x). И из этого получаем формулу для вычисления объёма тела вращения: V=π
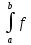 2(x)dx
2(x)dxПример. Найти объём шара радиуса R.
Решение. Шар получается при вращении полуокружности вокруг оси Ох. Уравнение верхней полуокружности имеет вид:
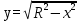 R ≤ x ≤ R.
R ≤ x ≤ R.Тогда по формуле для вычисления объёма тела вращения V=π
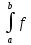 2(x)dx, будем иметь: V=π
2(x)dx, будем иметь: V=π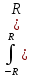 2-x2)dx=πR2
2-x2)dx=πR2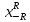 -
-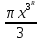 =2
=2 R3-
R3-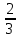 πR3=
πR3=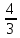 πR3
πR3
