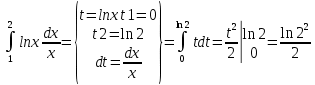Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 60
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Свойства интеграла с переменным верхним пределом.
Теорема 1. Пусть интегрируема на
Доказательство. Пусть
Функция ограничена на
Следовательно
Теорема 2. Пусть функция интегрируема на
Теорема 3.Пусть функция непрерывна на
, где
- 1 ... 7 8 9 10 11 12 13 14 15
Сформулируйте и докажите основную теорему интегрального исчисления. Приведите примеры использования формулы Ньютона-Лейбница при вычислении определенного интеграла.
Формула Ньютона- Лейбница
Теорема 4. (основная теорема интегрального исчисления)
Пусть f(x) - непрерывна на [a;b] и пусть Ф(x) - какая-либо первообразная этой функции, тогда
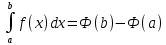
Док-во:
Пусть F(x) =
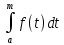 - первообразная функции f(m).
- первообразная функции f(m).Ф(x) и F(x) - отличаются на const C, т.е.
F(x) = Ф(x) + C
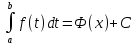
1) пусть x=a, тогда 0 = Ф(а) + С → С = - Ф(а)
пусть x=b, тогда
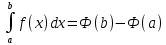 ч.т.д.
ч.т.д.- Сформулируйте теорему о замене переменной в определенном интеграле и теорему о вычислении определенного интеграла методом интегрирования по частям. Укажите особенность применения метода замены переменной в определенном интеграле. Приведите примеры.
-
Метод замены переменной.
Теорема 1.Пусть выполняются условия:
-
f(x) непрерывна на [a,b]. -
Отрезок [a,b] является множеством значений некоторой функции x=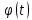 определена на отрезке [,] и имеющей на нем непрерывную производную.
определена на отрезке [,] и имеющей на нем непрерывную производную. -
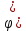 )=а
)=а 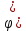 )=b
)=b
в этом случае справедлива формула замены переменной определенного интеграла
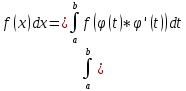
Замечание. Если при вычислении неопределенного интеграла с помощью замены мы должны были от новой переменной t возвращаться к старой переменной x, то при вычислении определенного интеграла этого можно не делать т.к. цель – найти число, которое согласно вышеприведенной формуле равно значению каждого из рассматриваемых интегралов.
Примеры:
2) Интегрирование по частям
Теорема 2.
Если функция u=u(x) и v=v(x) – непрерывна на [a,b] вместе со своими производными, то справедлива формула
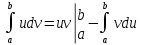
Пример.
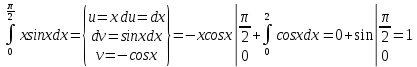
- Обобщите интеграл Римана на случай неограниченного промежутка. Введите понятие несобственного интеграла первого рода. Объясните способ его вычисления и обобщенную формулу Ньютона-Лейбница. Приведите примеры сходящегося и расходящегося интегралов.
Определение. Пусть функция f(x) задана в промежутке [a,+
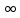 ) и интегрируема в любой его части [a,b] т.е. существует определенный интеграл
) и интегрируема в любой его части [a,b] т.е. существует определенный интеграл 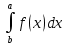 при любом b>a. Тогда, если существует конечный предел
при любом b>a. Тогда, если существует конечный предел 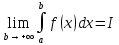 (3)
(3)То его называют несобственным интегралом первого рода или несобственным интегралом функции f(x) в промежутке [a,+
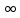 ) и обозначают символом
) и обозначают символом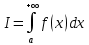 (4)
(4)Таким образом:
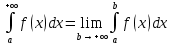 (5)
(5)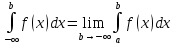
В этом случае говорят, что несобственный интеграл (4) существует или сходится. Если же предел (3) не существует или бесконечен то говорят что несобственный интеграл (4) не существует или расходится.
Несобственный интеграл с обоими бесконечными пределами определяется как сумма подобных интегралов т. е. справедливо равенство:
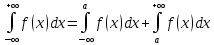
Замечание. Так как несобственный интеграл определяется как предел определенного интеграла, то на несобственный интеграл переносится все те свойства определенного интеграла, которые сохраняются при этом предельном переходе. Теорема о среднем, очевидно, здесь не выполняется.
Обобщенная формула Ньютона-Лейбница:
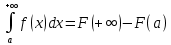
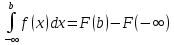
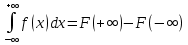
Где
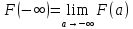
Примеры:
-
Исследовать сходимость интеграла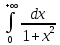
Решение:
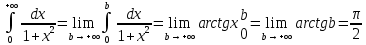
Т.е. интеграл сходится.
-
Исследовать сходимость интеграла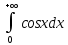
Решение:
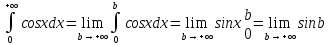
Но предел функции sinb при
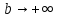 не существует, следовательно, интеграл расходится.
не существует, следовательно, интеграл расходится.-
Сформулируйте определение несобственного интеграла от неограниченной функции (второго рода). Объясните его геометрический смысл и правила вычисления. Опишите свойства этого интеграла.
Определение. Пусть функция f(x) определена и не ограничена на полуинтервале [a,b), причем она ограничена и интегрируема по Риману на любом отрезке [a,t],
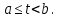 Тогда, если существует конечный предел
Тогда, если существует конечный предел 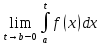
То он называется несобственным интегралом от функции f(x) на отрезке [a,b] и обозначается
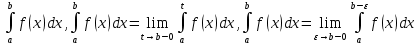
Геометрический смысл:
Если функция f неотрицательна и непрерывна на промежутке [a,b) то несобственный интеграл
 числено равен площади неограниченной области G:
числено равен площади неограниченной области G: 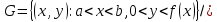
Несобственные интегралы 2-го рода легко переносятся многие свойства интеграла Римана:
Свойство 1. Пусть функция f непрерывна на полуинтервале [a,b) и пусть F- какая-либо первообразная функции f на [a,b)тогда
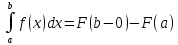
Свойство 2.Несобственный интеграл от алгебраической суммы функций равен алгебраической сумме их несобственных интегралов
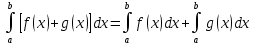
Свойство 3.Постоянный множитель можно выносить за знак несобственного интеграла