Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 64
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
4. При измельчении разбиения верхняя сумма Дарбу не возрастает, а нижняя сумма не убывает.
5.
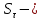
 =
= 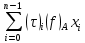 , где
, где 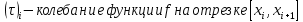
Множество{S} всех верхних сумм Дарбу отвечающих разбиению
 на отрезке ограничено снизу, а множество всех нижних сумм Дарбу ограничено сверху.
на отрезке ограничено снизу, а множество всех нижних сумм Дарбу ограничено сверху.Таким образом, существует точная нижняя грань множества всех верхних сумм и точная верхняя грань
 = inf
= inf  ,
, 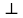 = sup
= sup 
 – верхний интеграл Дарбу
– верхний интеграл Дарбу 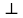 – нижний интеграл Дарбу.
– нижний интеграл Дарбу.Теорема (Критерий Дарбу) Для того, чтобы существовал интергал от функции на необходимо и достаточно, чтобы были равны верхний и нижний интегралы дарбу
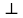 =
= . При этом I=
. При этом I=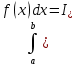 =
= 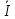
-
Сформулируйте критерий интегрируемости по Риману и следствие из него. Сформулируйте и докажите интегрируемость по Риману функции, непрерывной на отрезке и функции, монотонной на отрезке.
Теорема (Критерий Римана) Для того чтобы ограниченная на отрезке (а,b), функция была интегрируема (по Риману) на этом отрезке, необходимо и достаточно, чтобы

Следствие. Если функция f интегрируема, то не только ее интегральные суммы Римана
, но также и интегральные суммы Дарбу стремятся к ее интегралу, когда мелкость разбиения λ стремится к нулю.
Теорема. Если функция f(х) непрерывна на отрезке (a,b), то она интегрируема на этом отрезке.
Доказательство. Ограниченность
По теореме Кантора эта функция равномерно непрерывна на отрезке . Значит, для любого найдется такое , что для любых и , принадлежащих отрезку , из неравенства следует неравенство
Возьмем такое разбиение
Отсюда следует, что
Значит,
Теорема. Если функция f(х), монотонна на отрезке (a,b), то она интегрируема на этом отрезке.
Доказательство. Ограниченность на отрезке следует из свойств непрерывных функций.
Пусть возрастает на отрезке , т.е.
.
В силу монотонности имеем
Тогда
- Сформулируйте свойства определенного интеграла. Объясните свойство аддитивности интеграла и особенности вычисления определенного интеграла четной и нечетной функций по симметричному промежутку. Ответ проиллюстрируйте геометрически.
Свойства определенного интеграла:
-
Для любой функции f положим по определению: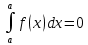 , а для функции, интегрируемой на отрезка [a,b]:
, а для функции, интегрируемой на отрезка [a,b]: 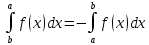 , a
, a -
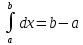
-
Если функция f(x) интегрируема на [a,b], то она интегрируема на [с,d] ⊂[a,b] -
Аддитивность. Пусть a.Если a -
Постоянный множитель можно вынести за знак определённого интеграла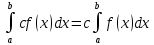
-
Определенный интеграл от алгебраической суммы равен алгебраической сумме их интегралов -
Если функция f(x) интегрируема на [a,b], неотрицательна(f(x) ≥0) и a ≥0 -
Если функции f и g интегрируемы на [a,b], для всех x∈[a,b] f(x) ≥g(x), то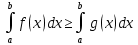 , то ест неравенство можно почленно интегрировать
, то ест неравенство можно почленно интегрировать -
Если функция f(x) интегрируема на [a,b], a -
Если функция f(x) интегрируема на [a,b], a f(x)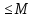 для любого x из [a,b], то
для любого x из [a,b], то
m(b-a)

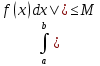 (b-a). Следствие: Если во всем промежутке имеет место неравенство
(b-a). Следствие: Если во всем промежутке имеет место неравенство 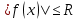 , то |
, то |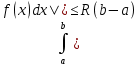
Пусть функция y=f(x) определена на отрезке [-a,a] и четна на этом отрезке. Тогда ее график симметричен относительно оси Oy. Если функция y=f(x) непрерывна на отрезке [-a,a] и является четной, то
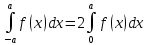
Пусть функция y=f(x) определена на отрезке [-a,a] и нечетна на этом отрезке. Тогда ее график симметричен относительно оси начала координат. Если функция y=f(x) непрерывна на отрезке [-a,a] и является нечетной, то
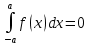
- 1 ... 7 8 9 10 11 12 13 14 15
Сформулируйте и докажите теорему о среднем значении для интеграла Римана, приведите её геометрическую интерпретацию.
Теорема: Теорема о среднем. Если функция f(x) непрерывна на [a,b], то существует такая точка ξ ∈[a,b], что
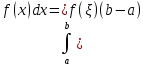 ,
, 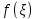 - среднее значение функции на отрезке
- среднее значение функции на отрезкеДоказательство:
Пусть a ≤
 ≤ М
≤ М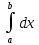
m
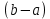 ≤
≤  ≤ М
≤ М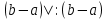
m≤
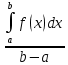 ≤ М
≤ Мm≤ η ≤ М
Между наименьшим и наибольшими значениями функции по т.Коши о промежуточных значениях функции обязательно найдется ξ ∈[a,b]= η
f(ξ )=
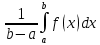 , следовательно
, следовательно 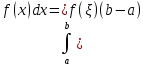
Геометрически: для площади криволинейной трапеции ограниченной сверху непрерывной кривой всегда существует равновеликий ей прямоугольник с тем же основание, а высота его равна одной из ординат этой кривой.
-
Введите понятие определенного интеграла с переменным верхним пределом. Сформулируйте его свойства и одно из них докажите.
Пусть функция f(x) интегрируема на отрезке [a, b],тогда по свойству 3 она интегрируема и на любом отрезке [a, х], где

Функция F определена на отрезке [a, b] и называется интегралом с переменным верхним пределом. Геометрически функция F(х) представляет собой площадь заштрихованной криволинейной трапеции , если F(х)>0.

