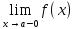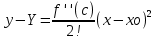Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 63
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0 ) > 0, то х0 является точкой возрастания функции. Если f ′ (x0 ) < 0, то х0 являыется точкой убывания функции.
Если f ′ (x0 ) = 0, а f ′′ (x0 ) 0 , то в т. х0 есть экстремум, а именно, если f ′′ (x0 ) > 0 , то минимум.
0 , то в т. х0 есть экстремум, а именно, если f ′′ (x0 ) > 0 , то минимум.
Пример: f(x) =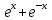 + 2 cos x - исследовать на экстремум
+ 2 cos x - исследовать на экстремум
Решение:
1) f ′ (x) =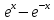 + 2 sin x =
+ 2 sin x = 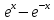 - 2 sin x
- 2 sin x
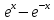 - 2 sin x = 0 x0 = 0 - стационарная точка
- 2 sin x = 0 x0 = 0 - стационарная точка
2)f ′′ (x) =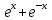 - 2 cos x , f ′′ (x0 ) = 0
- 2 cos x , f ′′ (x0 ) = 0
3)f ′′′ (x) =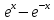 + 2 sin x , f ′′′ (x0 ) = 0
+ 2 sin x , f ′′′ (x0 ) = 0
4)f ′′′′ (x) =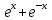 + 2 cos x f ′′′′ (x0 ) = 4 > 0 → по теореме 6 х0 - точка минимума.
+ 2 cos x f ′′′′ (x0 ) = 4 > 0 → по теореме 6 х0 - точка минимума.
Пусть Х - некоторое множество, входящее в область определения D(f) функции y=f(x).
Определение. Значение f(x0) функции y=f(x) в точке х0Х называется наибольшим (наименьшем) значением функции f(x) на множестве Х если для любой точки хХ выполнено неравенство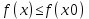 (
(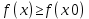 )
)
Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке
Чтобы найти наибольшее и наименьшее значения функции f(x) на отрезке [a,b] нужно
Алгоритм нахождения наименьшего и наибольшего значения на интервале.
Предположим, что функция ƒ(х) дифференцируема в любой точке интервала (а,b). Тогда, как известно, существует касательная к графику функции у = ƒ(х), проходящая через любую точку М(х,ƒ (х)) этого графика (а < х < В), причем эта касательная не параллельна оси Оу.
Определение 1. Будем говорить, что график функции у = ƒ(х) имеет на (а,b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а,b).
ТЕОРЕМА (достаточное условие выпуклости). Если функция у = ƒ(х) имеет на интервале (а, b) вторую производную и ƒ"(х) ≥0 (ƒ"(х) ≤0) во всех точках (а,b), то график функции у = ƒ(х) имеет на (а, b) выпуклость, направленную вниз(верх).
Доказательство.
Надо доказать, что график функции y=f(x) лежит не ниже любой касательной проведенной к графику функции.
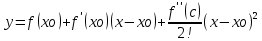
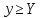 ч.т.д.
ч.т.д.
Замечание. Если ƒ”(х) = 0 всюду на (а,b), то у = ƒ(х) — линейная функция, т. е. график её есть прямая линия. В этом случае направление выпуклости можно считать произвольным.
ТЕОРЕМА . Пусть вторая производная функции у = ƒ(х), т. е. ƒ"(х), непрерывна и положительна (отрицательна) в точке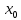 . Тогда существует такая окрестность точки Хо, в пределах которой график функции у = ƒ(х) имеет выпуклость, направленную вниз (вверх).
. Тогда существует такая окрестность точки Хо, в пределах которой график функции у = ƒ(х) имеет выпуклость, направленную вниз (вверх).
Пусть a,b и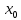 – некоторые числа, причем
– некоторые числа, причем 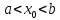 . Функция у=f(х) дифференцируема на (а,b), т. е. существует касательная к графику этой ф-ции во всех точках, абсциссы которых принадлежат интервалу (а,b). Пусть график ф-ции у=f(х) имеет определенное направление выпуклости на каждом их интервалов (
. Функция у=f(х) дифференцируема на (а,b), т. е. существует касательная к графику этой ф-ции во всех точках, абсциссы которых принадлежат интервалу (а,b). Пусть график ф-ции у=f(х) имеет определенное направление выпуклости на каждом их интервалов (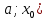 и (
и (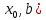 .
.
Опр. 2. Точка М(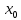 ,ƒ (
,ƒ (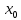 )) графика ф-ции у=f(х) называется
)) графика ф-ции у=f(х) называется
точкой перегиба этого графика, если существует такая окрестность точки , в пределах которой график ф-ции у=f(х) слева и справа от
, в пределах которой график ф-ции у=f(х) слева и справа от  имеет направления выпуклости
имеет направления выпуклости
Теорема. (необходимое условие точки перегиба). Если график ф-ции у=f(х) имеет перегиб в точке М( ,ƒ (
,ƒ ( )) и если ф-ция f(х) имеет в точке
)) и если ф-ция f(х) имеет в точке  непрерывную вторую производную, то
непрерывную вторую производную, то 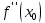 =0
=0
Точки М( ,ƒ (
,ƒ ( )) графика, для которых
)) графика, для которых 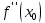 =0, называются критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке , для этого существуют достаточные условия перегиба.
=0, называются критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке , для этого существуют достаточные условия перегиба.
Доказательство (методом от противного).
Пусть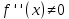 , для определеннности положим
, для определеннности положим 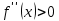 след-но по теореме (об устойчивости знака непрерывной функции) существует u(x0) в пределах которой
след-но по теореме (об устойчивости знака непрерывной функции) существует u(x0) в пределах которой 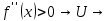 нет точек перегиба, а это противоположно условию теоремы ч.т.д.
нет точек перегиба, а это противоположно условию теоремы ч.т.д.
Теорема (первое достаточное условие точки перегиба). Пусть функция y=f(x) имеет вторую производную в некоторой окрестности точки х0 и f’’(x0)=0. Тогда, если в пределах указанной окрестности вторая производная f’’(x0)=0 имеет разные знаки слева и справа от x0, то график этой функции имеет перегиб в точке М(х0,f(x0)).
Теорема. (второе достаточное условие точки перегиба в терминах третьей производной).Если функция y=f(x) имеет в точке х0 конечную третью производную и при этом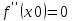 а
а 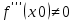 , то график этой функции имеет перегиб в точке M(x0,f(x0))
, то график этой функции имеет перегиб в точке M(x0,f(x0))
Доказательство:
Пусть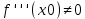 пусть
пусть 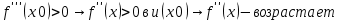
Так как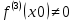 то по теореме о строгом возрастании (убывании) функции
то по теореме о строгом возрастании (убывании) функции 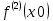 либо строго возрастает, либо строго убывает в точке х0 . По условию
либо строго возрастает, либо строго убывает в точке х0 . По условию 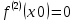 поэтому
поэтому 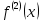 имеет разные знаки на интервалах
имеет разные знаки на интервалах 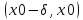 и
и 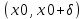 при некотором
при некотором 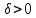 откуда используя теорему о первом достаточном условии наличия точек перегиба, заключаем что х0 точка перегиба функции f(x).
откуда используя теорему о первом достаточном условии наличия точек перегиба, заключаем что х0 точка перегиба функции f(x).
Говорят, что х=а является вертикальной асимптотой графика функции у=f(x), если хотя бы один из пределов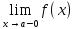
Если f ′ (x0 ) = 0, а f ′′ (x0 )
 0 , то в т. х0 есть экстремум, а именно, если f ′′ (x0 ) > 0 , то минимум.
0 , то в т. х0 есть экстремум, а именно, если f ′′ (x0 ) > 0 , то минимум.Пример: f(x) =
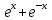 + 2 cos x - исследовать на экстремум
+ 2 cos x - исследовать на экстремумРешение:
1) f ′ (x) =
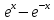 + 2 sin x =
+ 2 sin x = 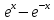 - 2 sin x
- 2 sin x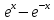 - 2 sin x = 0 x0 = 0 - стационарная точка
- 2 sin x = 0 x0 = 0 - стационарная точка2)f ′′ (x) =
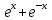 - 2 cos x , f ′′ (x0 ) = 0
- 2 cos x , f ′′ (x0 ) = 03)f ′′′ (x) =
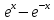 + 2 sin x , f ′′′ (x0 ) = 0
+ 2 sin x , f ′′′ (x0 ) = 04)f ′′′′ (x) =
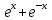 + 2 cos x f ′′′′ (x0 ) = 4 > 0 → по теореме 6 х0 - точка минимума.
+ 2 cos x f ′′′′ (x0 ) = 4 > 0 → по теореме 6 х0 - точка минимума.- 0>1 2 3 4 5 6 7 8 9 10 ... 15
Введите понятия наибольшего и наименьшего значений функции на отрезке. Сформулируйте правила нахождения наибольшего и наименьшего значений функции на отрезке и на интервале с помощью производной.
Пусть Х - некоторое множество, входящее в область определения D(f) функции y=f(x).
Определение. Значение f(x0) функции y=f(x) в точке х0Х называется наибольшим (наименьшем) значением функции f(x) на множестве Х если для любой точки хХ выполнено неравенство
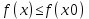 (
(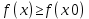 )
)Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке
Чтобы найти наибольшее и наименьшее значения функции f(x) на отрезке [a,b] нужно
-
Найти все точки «подозрительные» на экстремум. -
Выбрать из них те точки, которые принадлежат отрезку [a,b] -
Вычислить значения функции во всех этих точках, а также значения на концах отрезка f(a) и f(b). -
Выбрать из всех полученных значений наибольшее и наименьшее.
Алгоритм нахождения наименьшего и наибольшего значения на интервале.
-
Находим производную f’(x). -
f’(x)=0 -
Находим стационарную точку выбираем (a,b) -
Если точки стационарная одна, нужно исследовать ее на экстремумы. -
Если m max-наибольшее значение, m min-наименьшее значение -
Записать ответ.
-
Введите понятие выпуклости вниз (вверх) функции на промежутке. Сформулируйте и докажите достаточные условия выпуклости функции вниз (вверх). Проиллюстрируйте их на примере.
Предположим, что функция ƒ(х) дифференцируема в любой точке интервала (а,b). Тогда, как известно, существует касательная к графику функции у = ƒ(х), проходящая через любую точку М(х,ƒ (х)) этого графика (а < х < В), причем эта касательная не параллельна оси Оу.
Определение 1. Будем говорить, что график функции у = ƒ(х) имеет на (а,b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а,b).
ТЕОРЕМА (достаточное условие выпуклости). Если функция у = ƒ(х) имеет на интервале (а, b) вторую производную и ƒ"(х) ≥0 (ƒ"(х) ≤0) во всех точках (а,b), то график функции у = ƒ(х) имеет на (а, b) выпуклость, направленную вниз(верх).
Доказательство.
-
Для определеенности рассмотрим случай f ’’(x)≥на (а,b). Пусть х0 любая точка из (а,b).
Надо доказать, что график функции y=f(x) лежит не ниже любой касательной проведенной к графику функции.
-
Уравнение касательной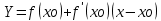 к графику в точке хо.
к графику в точке хо. -
Разложим функцию y=f(x) по формуле Тейлора при n=1
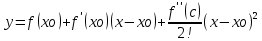
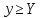 ч.т.д.
ч.т.д.Замечание. Если ƒ”(х) = 0 всюду на (а,b), то у = ƒ(х) — линейная функция, т. е. график её есть прямая линия. В этом случае направление выпуклости можно считать произвольным.
ТЕОРЕМА . Пусть вторая производная функции у = ƒ(х), т. е. ƒ"(х), непрерывна и положительна (отрицательна) в точке
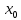 . Тогда существует такая окрестность точки Хо, в пределах которой график функции у = ƒ(х) имеет выпуклость, направленную вниз (вверх).
. Тогда существует такая окрестность точки Хо, в пределах которой график функции у = ƒ(х) имеет выпуклость, направленную вниз (вверх).-
Сформулируйте определение точки перегиба графика функции, проиллюстрируйте его на примерах. Сформулируйте и докажите необходимое условие перегиба графика функции.
Пусть a,b и
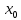 – некоторые числа, причем
– некоторые числа, причем 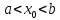 . Функция у=f(х) дифференцируема на (а,b), т. е. существует касательная к графику этой ф-ции во всех точках, абсциссы которых принадлежат интервалу (а,b). Пусть график ф-ции у=f(х) имеет определенное направление выпуклости на каждом их интервалов (
. Функция у=f(х) дифференцируема на (а,b), т. е. существует касательная к графику этой ф-ции во всех точках, абсциссы которых принадлежат интервалу (а,b). Пусть график ф-ции у=f(х) имеет определенное направление выпуклости на каждом их интервалов (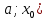 и (
и (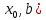 .
.Опр. 2. Точка М(
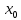 ,ƒ (
,ƒ (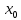 )) графика ф-ции у=f(х) называется
)) графика ф-ции у=f(х) называется
точкой перегиба этого графика, если существует такая окрестность точки
 , в пределах которой график ф-ции у=f(х) слева и справа от
, в пределах которой график ф-ции у=f(х) слева и справа от  имеет направления выпуклости
имеет направления выпуклостиТеорема. (необходимое условие точки перегиба). Если график ф-ции у=f(х) имеет перегиб в точке М(
 ,ƒ (
,ƒ ( )) и если ф-ция f(х) имеет в точке
)) и если ф-ция f(х) имеет в точке  непрерывную вторую производную, то
непрерывную вторую производную, то 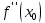 =0
=0Точки М(
 ,ƒ (
,ƒ ( )) графика, для которых
)) графика, для которых 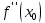 =0, называются критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке , для этого существуют достаточные условия перегиба.
=0, называются критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке , для этого существуют достаточные условия перегиба.Доказательство (методом от противного).
Пусть
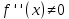 , для определеннности положим
, для определеннности положим 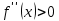 след-но по теореме (об устойчивости знака непрерывной функции) существует u(x0) в пределах которой
след-но по теореме (об устойчивости знака непрерывной функции) существует u(x0) в пределах которой 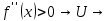 нет точек перегиба, а это противоположно условию теоремы ч.т.д.
нет точек перегиба, а это противоположно условию теоремы ч.т.д.- 1 ... 4 5 6 7 8 9 10 11 ... 15
Сформулируйте и докажите достаточные условия перегиба графика функции в терминах второй производной и в терминах третьей производной. Проиллюстрируйте их на примерах.
Теорема (первое достаточное условие точки перегиба). Пусть функция y=f(x) имеет вторую производную в некоторой окрестности точки х0 и f’’(x0)=0. Тогда, если в пределах указанной окрестности вторая производная f’’(x0)=0 имеет разные знаки слева и справа от x0, то график этой функции имеет перегиб в точке М(х0,f(x0)).
Теорема. (второе достаточное условие точки перегиба в терминах третьей производной).Если функция y=f(x) имеет в точке х0 конечную третью производную и при этом
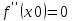 а
а 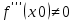 , то график этой функции имеет перегиб в точке M(x0,f(x0))
, то график этой функции имеет перегиб в точке M(x0,f(x0))Доказательство:
Пусть
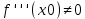 пусть
пусть 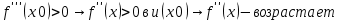
Так как
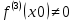 то по теореме о строгом возрастании (убывании) функции
то по теореме о строгом возрастании (убывании) функции 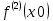 либо строго возрастает, либо строго убывает в точке х0 . По условию
либо строго возрастает, либо строго убывает в точке х0 . По условию 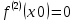 поэтому
поэтому 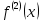 имеет разные знаки на интервалах
имеет разные знаки на интервалах 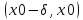 и
и 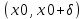 при некотором
при некотором 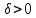 откуда используя теорему о первом достаточном условии наличия точек перегиба, заключаем что х0 точка перегиба функции f(x).
откуда используя теорему о первом достаточном условии наличия точек перегиба, заключаем что х0 точка перегиба функции f(x).- Сформулируйте определения вертикальной и наклонной асимптот графика функции. Докажите теорему, выражающую необходимые и достаточные условия существования наклонной асимптоты. Объясните правила нахождения асимптот (вертикальной и наклонной). Приведите примеры.
Говорят, что х=а является вертикальной асимптотой графика функции у=f(x), если хотя бы один из пределов