Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 77
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оглавление
1.Опишите задачи, приводящие к понятию производной. Сформулируйте определение производной функции в точке, определение односторонних производных. Объясните алгоритм нахождения производной с помощью определения. 1
2.Сформулируйте определения дифференцируемости и дифференциала функции в точке. Докажите теорему и следствие из неё о связи дифференцируемости и непрерывности функции в точке. 1
3.Сформулируйте и докажите теорему, выражающую необходимые и достаточные условия дифференцируемости функции в точке. 2
4.Опишите понятие касательной к графику функции в точке. Объясните геометрический и физический смысл производной и дифференциала функции в точке. 2
5.Сформулируйте и докажите теорему, выражающую правила вычисления производной. Приведите примеры. Опишите свойства дифференциала функции. 3
6.Сформулируйте и докажите теорему о производной обратной функции. Объясните её геометрический смысл. Приведите примеры её применения для вывода производных обратных тригонометрических функций. 3
7.Сформулируйте теорему о производной сложной функции одной переменной. Приведите примеры её применения. Объясните инвариантность формы первого дифференциала. 3
9.Введите понятие производной второго, третьего и т. д., n-го порядка. Приведите примеры. Сформулируйте теорему о производных высших порядках суммы и произведения функций. Проиллюстрируйте их примерами. 4
10.Введите понятие дифференциала второго, третьего и т. д., n-го порядка функции одной переменной. Докажите формулу для дифференциала n-го порядка. Сформулируйте свойства дифференциалов высших порядков. Приведите примеры. 5
11.Сформулируйте и докажите теорему Ферма. Приведите её геометрическую интерпретацию. 5
12.Сформулируйте и докажите теорему Ролля о среднем значении, приведите её геометрическую интерпретацию и объясните условия применимости. 6
13.Сформулируйте и докажите теорему Лагранжа о среднем значении и следствие из неё. Объясните геометрический смысл теоремы. 7
14.Сформулируйте правило Лопиталя раскрытия неопределенностей. Объясните его применение при вычислении пределов функций в случаях разных видов неопределенностей. 8
15.Приведите вывод формулы Тейлора для произвольной функции с остаточным членом в форме Лагранжа. Объясните получение формулы Маклорена. 8
16.Объясните разложение основных элементарных функций (????????, sin ????, cos ????, ln ????, ????rctg ????) по формуле Маклорена. 9
17. Введите понятие монотонной функции. Сформулируйте и докажите признак монотонности функции, объясните его геометрический смысл. Проиллюстрируйте его применение на конкретном примере. 9
18.Введите понятие точек экстремума (максимума и минимума) и экстремума функции. Сформулируйте необходимое условие экстремума и проиллюстрируйте его геометрически. Сформулируйте и докажите достаточное условие экстремума функции в терминах первой производной. 10
19.Сформулируйте и докажите достаточное условие существования экстремума в терминах второй производной. Опишите условия его применимости и проиллюстрируйте на примере. 11
20.Сформулируйте теорему, выражающую достаточные условия экстремума функции, не дифференцируемой в данной точке. Приведите пример. 11
21.Введите понятия точки возрастания и точки убывания функции. Сформулируйте достаточные условия экстремума в терминах высших производных. Объясните процесс исследования функции на экстремум с помощью высших производных. Приведите пример. 12
22.Введите понятия наибольшего и наименьшего значений функции на отрезке. Сформулируйте правила нахождения наибольшего и наименьшего значений функции на отрезке и на интервале с помощью производной. 12
23.Введите понятие выпуклости вниз (вверх) функции на промежутке. Сформулируйте и докажите достаточные условия выпуклости функции вниз (вверх). Проиллюстрируйте их на примере. 13
24.Сформулируйте определение точки перегиба графика функции, проиллюстрируйте его на примерах. Сформулируйте и докажите необходимое условие перегиба графика функции. 14
25.Сформулируйте и докажите достаточные условия перегиба графика функции в терминах второй производной и в терминах третьей производной. Проиллюстрируйте их на примерах. 14
26.Сформулируйте определения вертикальной и наклонной асимптот графика функции. Докажите теорему, выражающую необходимые и достаточные условия существования наклонной асимптоты. Объясните правила нахождения асимптот (вертикальной и наклонной). Приведите примеры. 15
28.Сформулируйте определение частной производной функции трех переменных в точке. Введите понятие частного и полного дифференциалов функции в точке. Приведите примеры нахождения частных производных и частных дифференциалов функции трех переменных. 16
29.Введите понятие частных производных второго и третьего порядков (чистых и смешанных). Приведите примеры нахождения частных производных второго и третьего порядков. 16
30.Сформулируйте теорему о равенстве смешанных частных производных второго порядка. Приведите примеры. 16
31.Введите понятие дифференциалов высших порядков функции двух переменных. Опишите процесс нахождения дифференциалов второго и третьего порядков. Объясните, в чем особенность нахождения дифференциала второго порядка сложной функции. Приведите примеры. 16
33.Сформулируйте задачу восстановления функции по ее производной. Объясните понятие первообразной функции. Приведите примеры. Докажите основное свойство первообразных. Сформулируйте правила нахождения первообразных и проиллюстрируйте их. 18
34.Введите понятие неопределенного интеграла и объясните его геометрический смысл. Сформулируйте и докажите основные свойства неопределенного интеграла. 19
35.Опишите основные методы вычисления неопределенного интеграла. Приведите примеры. Объясните, в каких случаях применяется метод интегрирования по частям и метод подведения под знак дифференциала. Что означает приведение интеграла к самому себе? 19
36.Объясните, что такое рациональная дробь, правильная (неправильная) дробь, элементарная (простейшая) дробь. Опишите схему интегрирования правильных рациональных дробей. Проиллюстрируйте на конкретном примере. 20
37.Опишите типы элементарных (простейших) рациональных дробей и сформулируйте правила их интегрирования. Приведите примеры. Опишите общую схему интегрирования рациональных функций. 21
38.Объясните правила интегрирования рациональных тригонометрических выражений, применение универсальной тригонометрической подстановки и формул тригонометрии, правила вычисления интегралов вида . Приведите примеры. 21
39.Сформулируйте задачи, приводящие к понятию определенного интеграла, и объясните метод их решения. Введите понятия интегральной суммы Римана и понятие определенного интеграла. Сформулируйте необходимое условие интегрируемости по Риману и докажите его. 22
40.Опишите понятия верхней и нижней сумм Дарбу. Сформулируйте их свойства. Введите понятия верхнего и нижнего интегралов Дарбу. Сформулируйте критерий интегрируемости Дарбу. 23
41.Сформулируйте критерий интегрируемости по Риману и следствие из него. Сформулируйте и докажите интегрируемость по Риману функции, непрерывной на отрезке и функции, монотонной на отрезке. 23
42.Сформулируйте свойства определенного интеграла. Объясните свойство аддитивности интеграла и особенности вычисления определенного интеграла четной и нечетной функций по симметричному промежутку. Ответ проиллюстрируйте геометрически. 23
43.Сформулируйте и докажите теорему о среднем значении для интеграла Римана, приведите её геометрическую интерпретацию. 24
m≤ η ≤ М 24
44.Введите понятие определенного интеграла с переменным верхним пределом. Сформулируйте его свойства и одно из них докажите. 24
45.Сформулируйте и докажите основную теорему интегрального исчисления. Приведите примеры использования формулы Ньютона-Лейбница при вычислении определенного интеграла. 25
46.Сформулируйте теорему о замене переменной в определенном интеграле и теорему о вычислении определенного интеграла методом интегрирования по частям. Укажите особенность применения метода замены переменной в определенном интеграле. Приведите примеры. 25
47.Обобщите интеграл Римана на случай неограниченного промежутка. Введите понятие несобственного интеграла первого рода. Объясните способ его вычисления и обобщенную формулу Ньютона-Лейбница. Приведите примеры сходящегося и расходящегося интегралов. 26
48.Сформулируйте определение несобственного интеграла от неограниченной функции (второго рода). Объясните его геометрический смысл и правила вычисления. Опишите свойства этого интеграла. 26
49.Опишите способы вычисления площади фигуры с помощью определенного интеграла в декартовых координатах. Приведите примеры. 27
50.Опишите способ вычисления объема тела вращения с помощью определенного интеграла в декартовых координатах. Приведите пример. 27
- Опишите задачи, приводящие к понятию производной. Сформулируйте определение производной функции в точке, определение односторонних производных. Объясните алгоритм нахождения производной с помощью определения.
-
И. Ньютон (1643-17270) – открыл общий способ описания связи между S (t) и V(t)
Пусть S=S(t) – закон прямолинейного движения матер. точки.
∆S = S(t+∆t) - S(t)
∆S/∆t – V ср.скорость движения точки
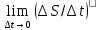 - V мгн (мгновенная скорость точки в данный момент времени)
- V мгн (мгновенная скорость точки в данный момент времени)-
Задача о проведении касательной к произвольной прямой. Г.В.Лейбниц (1646-1717)
М0(х0, f(х0)) , y=kx+b
∆y = f(х0+∆x)- f(х0)
tga= ∆y/∆x
ф- угол между касательной и положительным направлением ох.
Будем двигать М’ по кривой к точке М0. Секущая займет некое предельное отношение
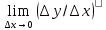 = tgф
= tgфОбе эти задачи приводят нас к одной и той же матем.операции – операции придельного перехода.
Пусть f(x) определена в некоторой окрестности U(x0), точки х0. И пусть точка х∈ U(x0), х-произвольная точка, тогда если
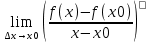 , то он называется производной функции f(x) в точке х0.
, то он называется производной функции f(x) в точке х0.Пусть f(x) определена в левосторон.(правосторон) окрестности точки х0 и пусть х произвольная точка, принадлежащая этой окрестности. Если
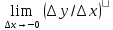 (
(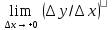 ), то он называется левоторон(правосторон.) производной функции f(x) в точке х0.
), то он называется левоторон(правосторон.) производной функции f(x) в точке х0. Алгоритм нахождения производной с помощью определения:
-
x0+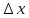 - даем приращение в т.х0
- даем приращение в т.х0 -
f(х0+∆x)- f(х0)-находим приращение функции -
составляем отношение(разность)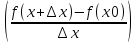
-
Находим предел разностного отношения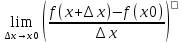
- Сформулируйте определения дифференцируемости и дифференциала функции в точке. Докажите теорему и следствие из неё о связи дифференцируемости и непрерывности функции в точке.
Функция у=f(x), определенная в некоторой окрестности U(х
0) точки х0, х0 ∈ R называется дифференцируемой в точке х0, если ее приращение в этой точке х0, представлено в виде
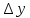 = А
= А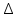 х+ о
х+ о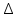 х,
х, 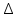 х→0, А= const, о
х→0, А= const, о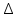 х-бм более высокого порядка от
х-бм более высокого порядка от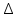 х
хЛинейная функция А
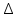 х ( от переменной
х ( от переменной 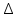 х) называется дифференциалом функции f в точке х0 и обозначается df(х0) или короче dy
х) называется дифференциалом функции f в точке х0 и обозначается df(х0) или короче dyТеорема: Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.
Док-во:
Пусть f(x) дифференцируема в точке х0 =>
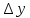 = А
= А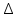 х+ 0
х+ 0 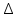 х (перейдем к пределу
х (перейдем к пределу 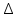 х→0)
х→0) 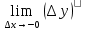 =
= 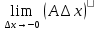 +
+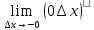 =0
=0=> f(x) непрерывна в точке х0, чтд (малому приращению аргумента соответсвует ммалое приращение функции.
Следствие:Если функция в некоторой точке х0 имеет производную, то она непрерывна в этой точке.
Док-во: ⅃ существует f ‘ (x0) => f(x) дифференцируема в точке x0 => эта функция непрерывна в этой точке.
- 1 2 3 4 5 6 7 8 9 ... 15
Сформулируйте и докажите теорему, выражающую необходимые и достаточные условия дифференцируемости функции в точке.
Теорема
Для того чтобы функция f(x) была дифференцируемой в некоторой точке х0, необходимо и достаточно, чтобы функция f(x) имела в этой точке производную f’(x) и тогда: dy= f’(x)*dx.
Доказательство:
-
Необходимость.
Пусть f(x) – дифференцируема в точке х0, тогда по определению:
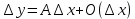 ,
, 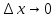 . Разделим обе части на
. Разделим обе части на 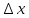 .
. 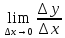 =
=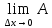 +
+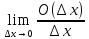 .
.Следовательно f’(x0)=А+0, откуда f’(x)=А.
-
Достаточность.
Пусть f’(x0) =(по опр)
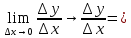 f’(x0)+
f’(x0)+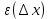 , где
, где 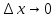 .
.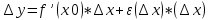 . Полагая, что
. Полагая, что 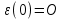 , получим
, получим 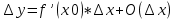 при
при 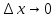 .,
., 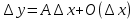 при
при 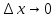 Следовательно f(x) дифференцируема в точке х0.
Следовательно f(x) дифференцируема в точке х0.- Опишите понятие касательной к графику функции в точке. Объясните геометрический и физический смысл производной и дифференциала функции в точке.
Опр1. Если существует (конечный предел k(Δх))
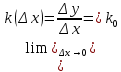 , то прямая определенная уравнением y=k0(x-x0)+y0 называется наклонной касательной к графику функции
, то прямая определенная уравнением y=k0(x-x0)+y0 называется наклонной касательной к графику функции
y=f(x) в точке x0.
Уравнение касательной y=f’(x0)(x-x0)+f(x0) в случае конечной производной в точке.
Если
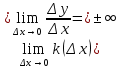 , то в этом случае существует вертикальная касательная х=х0.
, то в этом случае существует вертикальная касательная х=х0.Опр2. Предельное положение секущей М0М при Δх→0 или, что то же при М→М0 называется касательной к графику функции f в точке М0.
F’(х0)=tgφ – геометрический смысл производной в точке х0 есть tg угла, образованного касательной с положительным направлением оси Ох.
Y=y0+f’(x0), (y0=f(x0)) – уравнение касательной
y-y0=f’(x0)
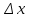 (
(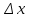 =dx)
=dx)У-у0=dy – геометрический смысл дифференциала – это есть прирощение ординаты касательной, проведенной к графику функции в точке М0 с абсциссой х0.
Физический смысл производной и дифференциала.
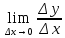 - скорость изменения одной переменной величины относительно другой (у относительно х) в точке х0.
- скорость изменения одной переменной величины относительно другой (у относительно х) в точке х0.На интерпретации производной, как скорости изменения величины, относительно другой и основано в применении производной при изучении физических явлений и процессов.
Дифференциал. Δу=А* Δх+0(Δх), Δх→0
У*у0 ≈dy 0(Δх)- погрешность
Применение дифференциала функции в физике основано на том, что замена приращения функции дифференциалом позволяет заменить любую дифференцируемую в точке х0 функцию, линейной.
- 1 2 3 4 5 6 7 8 9 ... 15
