Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 74
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теорема 2 (теорема Ролля). Пусть функция f(х):
-
непрерывна на отрезке [а, b]; -
имеет в каждой точке интервала (а, b) конечную или определенного знака бесконечную производную; -
принимает равные значения на концах отрезка, т. е. f(a) = f(b). Тогда существует хотя бы одна такая точка ξ (читается «кси»), а < ξ < b, что f ’(ξ ) = 0.
Доказательство.
Если для любой точки х интервала (а, b) выполняется равенство f(х) = f(a) = f(b), то функция f является постоянной на этом интервале и поэтому таких точек ξ € (а, b) бесконечно много f '(ξ) = 0.
Пусть существует точка х0 € (а, b), для которой f(x0) ≠ f(a), например, f(х0)>f(a). Согласно теореме Вейерштрасса о достижимости непрерывной на отрезке функцией своих наибольшего и наименьшего значений, существует такая точка ξ [а, b], в которой функция f принимает наибольшее значение.
f(ξ) ≥f(х0) > f(a) = f(b).
Поэтому ξ ≠ а и ξ ≠ b, т. е. точка ξ принадлежит интервалу (а, b) и функция f принимает в ней наибольшее значение. Следовательно, согласно теореме Ферма, выполняется равенство f '(ξ) = 0.
Геометрический смысл теоремы Ролля состоит в том, что на графике функции, удовлетворяющей условиям теоремы Ролля, имеется по крайней мере одна точка, в которой касательная параллельна оси ОХ
- Сформулируйте и докажите теорему Лагранжа о среднем значении и следствие из неё. Объясните геометрический смысл теоремы.
Если функция f(x) непрерывна на отрезке [a,b] и в любой точке интервала (a,b) имеет конечную или определенного знака бесконечную производную, то в этом интервале (a,b) существует, по крайней мере, одна точка
ξ ∈(a,b) такая, что выполняется равенство f(b)-f(a)=f ‘(ξ)(b-a) – формула конечных приращений Лагранжа
-
Р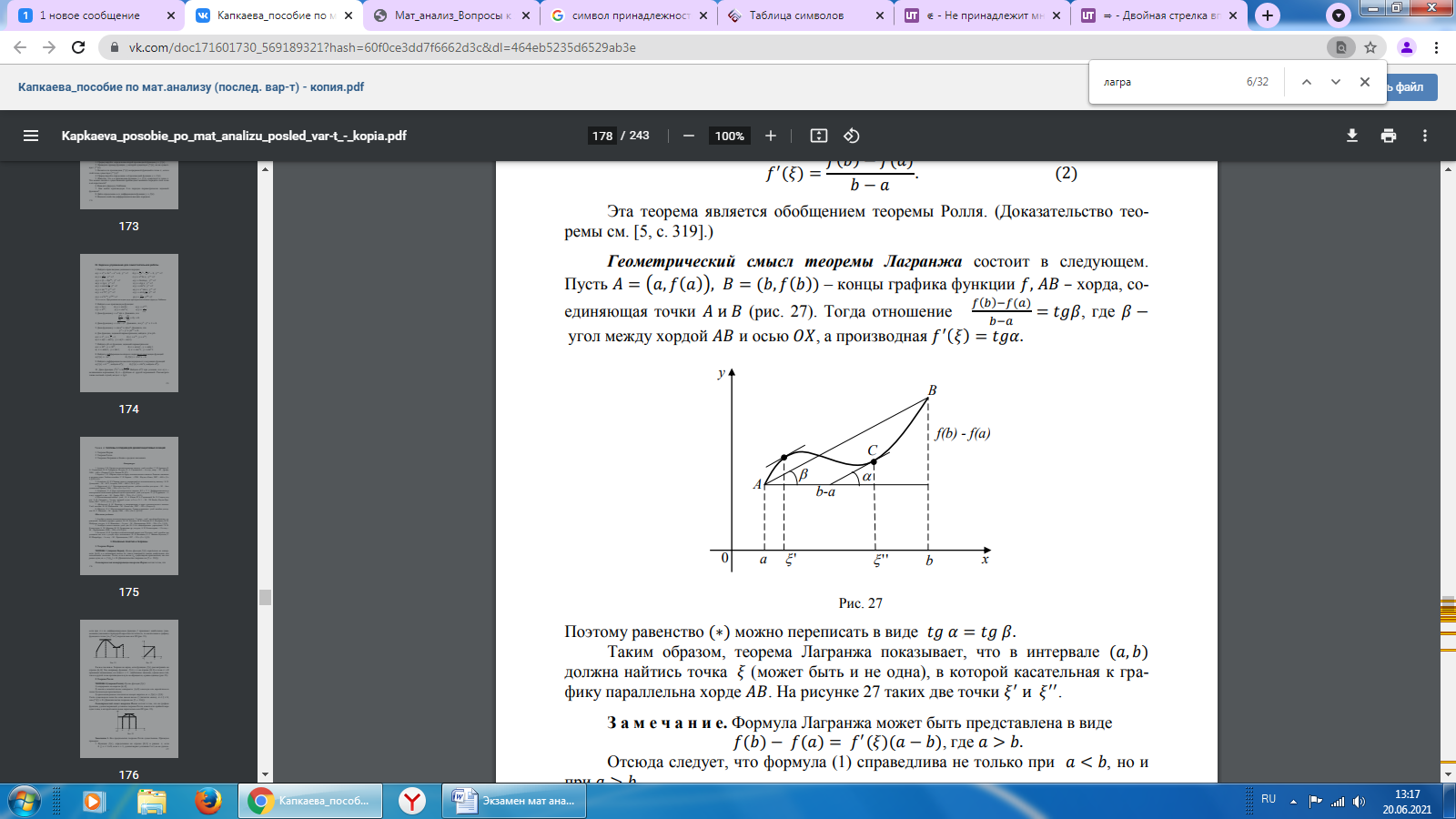 ассмотрим вспомогательную функцию F(x)= f(x) - λ(x), такую что F(a)= F(b) тогда f (a) - λ a= f (b) - λ b ⇒ λ=
ассмотрим вспомогательную функцию F(x)= f(x) - λ(x), такую что F(a)= F(b) тогда f (a) - λ a= f (b) - λ b ⇒ λ= 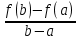
-
Для функции F(x) выполняются все условия т. Ролля:
-
f(x) непрерывна, как сумма двух непрерывных функций -
f(x) дифференцируема как сумма диф. Функций -
F(a)= F(b) выбрали ⇒ существует точка Ψ∈(a,b), F ‘(Ψ)=0
Продифференцируем F(x): F ‘(x)= f ‘(x)- λ=0 ⇒ f ‘(x) =λ,
f ‘(x) = λ=
 ч.т.д.
ч.т.д. Геометрический смысл теоремы Лагранжа состоит в следующем. Теорема Лагранжа показывает, что в интервале (a,b) существует по крайней мере одна точка в которой касательная к графику функций параллельна хорде, соединяющей концы кривой .
Следствие 1
Если функция непрерывна на некотором промежутке конечном или бесконечном и во всех его внутренних точках имеет производную равную нулю, то функция на этом промежутке является const
Док-во
Это следствие имеет наглядную механическую интерпретацию: если функция y=f (x) является законом движения материальной точки по прямой, x-время, y-расстояние от начала отсчета на прямой, то условие
f ‘(x)=0 для всех x∈(a,b) означает, что скорость рассматриваемой точки в течение интервала времени (a,b)все время равна нулю, т. е. точка неподвижна, но тогда за это время положение точки, а потому и пройденный ею путь не изменятся. Это и означает, что функция f(x) постоянна на интервале (a,b).
Следствие 2
Если f(x) и g(x) непрерывны на некотором промежутке и во всех его внутренних точках имеют равные производные, т.е. f ‘(x) = g’(x). То эти функции отличаются на const, т.е. f (x) = g(x)+с
Док-во
Рассмотрим F(x)= f(x) - g(x), которая удовлетворяет условию теоремы, т.е. F’(x)= 0 ⇒ F(x)= с ⇒ f(x) - g(x)=с ⇒ f (x) = g(x)+с ч.т.д.
- 1 2 3 4 5 6 7 8 9 ... 15
Сформулируйте правило Лопиталя раскрытия неопределенностей. Объясните его применение при вычислении пределов функций в случаях разных видов неопределенностей.
Неопределенность вида
1)функции f (x) и g(x)и определены в промежутке [a, b)
2)
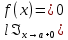 .
. 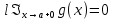
3) cуществуют в промежутке [a, b) конечные производные f ‘(x) и g’(x)
4) существует (конечный или бесконечный) предел
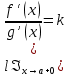 Тогда существует
Тогда существует 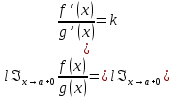
Пример 1:
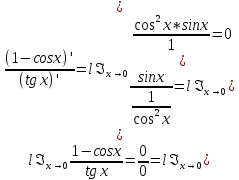
Неопределенность вида
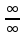
1)функции f (x) и g(x)и определены в промежутке [a, b)
2)
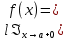 ∞.
∞. 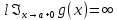
3) cуществуют в промежутке [a, b) конечные производные f ‘(x) и g’(x) , причем g’(x)≠0 ;
4) существует (конечный или бесконечный) предел
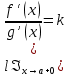 Тогда и
Тогда и 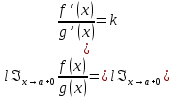
Пример 1 :
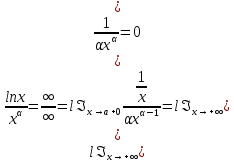
(α >0)
Другие виды неопределенностей (0*∞),
 (
(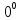 ),
), 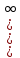 )
)При раскрытии других видов неопределенностей следует сначала свести
 их к виду 0
их к виду 00
или ∞, а затем применить правило Лопиталя.

-
Приведите вывод формулы Тейлора для произвольной функции с остаточным членом в форме Лагранжа. Объясните получение формулы Маклорена.
Rn(x)- остаточный члент формулы Тейлора
Пусть f(x) – дифф-ма в т. x0 и имеет производные до порядка (n+1) включительно, тогда :
Rn(x)=
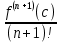 * (x-x0)n+1 – остаточный член ϕ1 в формуле Лагранжа
* (x-x0)n+1 – остаточный член ϕ1 в формуле ЛагранжаС-точка между x и x0
f(x)=f(x0) +
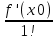 (x- x0) +
(x- x0) + 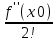 (x- x0)2 +…+
(x- x0)2 +…+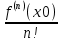 (x- x0)n +
(x- x0)n + 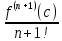 (x- x0)n+1 - формула Тейлора с остаточным членом в форме Лагранжа .
(x- x0)n+1 - формула Тейлора с остаточным членом в форме Лагранжа .Pn(x)=Pn(0) +
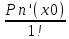 (x- x0) +
(x- x0) + 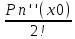 (x- x0)2 +…+
(x- x0)2 +…+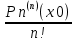 (x- x0)n - формула Тейлора для многочлена.
(x- x0)n - формула Тейлора для многочлена.Если x0=0, то получаем
Pn(x)=Pn(0) +
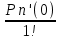 x +
x + 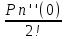 x2 +…+
x2 +…+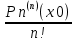 xn
xn-
Объясните разложение основных элементарных функций (????????, sin ????, cos ????, ln ????, ????rctg ????) по формуле Маклорена.
f(x)=ex. Так как f(x)=f '(x)= f '' (x)=…= f(n+1)(x)=ex ; f(0)=f '(0)= f '' (0)=…= f(n+1)(0)=1, то формула Маклорена имеет вид
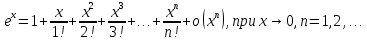
f(x)=sinx. Так как f(n)(x)=sin(x+n
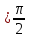 ); f(n)(0)=sin(n
); f(n)(0)=sin(n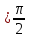 )=
)=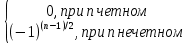 , то формула Маклорена имеет вид sinx=
, то формула Маклорена имеет вид sinx=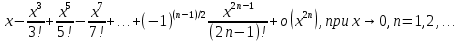
f(x)=cosx. Так как f(n)(x)=cos(x+n
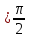 ); f(n)(0)=cos(n
); f(n)(0)=cos(n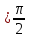 )=
)=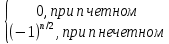 , то формула Маклорена имеет вид cosx=
, то формула Маклорена имеет вид cosx=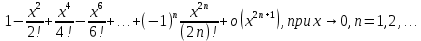
f(x)=ln(1+x). Так как f(n)(x)=
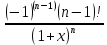 ; f(n)(0)=
; f(n)(0)=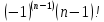 , то формула Маклорена имеет вид ln(1+x)=
, то формула Маклорена имеет вид ln(1+x)=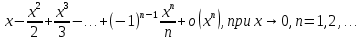
f(x)=arctgx, то формула Маклорена имеет вид arctgx=
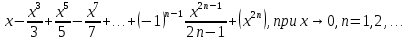
- 1 2 3 4 5 6 7 8 9 ... 15
