Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 75
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
или 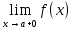 был равен
был равен 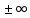 .
.
Говорят, что прямая у=kx+b является наклонной асимптотой графика функции у=f(x) при х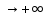 , если f(x) представима в виде: f(x)=kx+b+
, если f(x) представима в виде: f(x)=kx+b+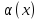 , где
, где 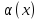 , бесконечно-малая функция, т.е
, бесконечно-малая функция, т.е 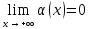 .
.
Теорема (о существовании наклонной асимптоты)
Для того чтобы график функции у=f(x) имел при х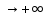 наклонную асимптоту необходимо и достаточно, чтобы существовали два предела:
наклонную асимптоту необходимо и достаточно, чтобы существовали два предела:
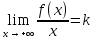 (1)
(1)
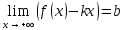 (2)
(2)
Доказательство:
Пусть график функции у=f(x) имеет наклонную асимптоту. Нужно доказать, что существуют два предела (1) и (2). По определению наклонной асимптоты имеем: f(x)=kx+b+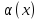 , где
, где 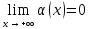 . Найдем:
. Найдем:
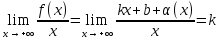 (1)
(1)
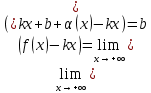 (2)
(2)
Даны два предела (1) и (2). Нужно доказать, что f(x)=kx+b+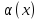 . Из (2)
. Из (2)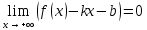 , означает что
, означает что 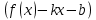 – бесконечно малая функция. Обозначим ее через
– бесконечно малая функция. Обозначим ее через 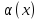 =
=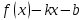 . Следовательно, f(x)=kx+b+
. Следовательно, f(x)=kx+b+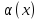 , откуда следует, что у=f(x) – имеет наклонную асимптоту.
, откуда следует, что у=f(x) – имеет наклонную асимптоту.
Схему полного исследования функции с помощью производной и построения её графика.
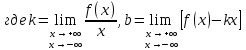
Пусть в некоторой окрестности точки (х0,y0,z0) задана функция u=u(х,y,z), фиксируя переменные y и z: y=y0, z=z0 , получим функцию одной переменной х: u=u(х,y0,z0). Обычная производная этой функции по х в точке х0 называется частной производной функции.
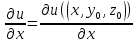
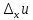 = u(x0+
= u(x0+ , y0,z0)-u(х0,y0,z0) – приращение функции u по переменной x
, y0,z0)-u(х0,y0,z0) – приращение функции u по переменной x
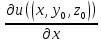 =
=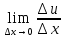
Пусть u=u(х,y,z), тогда выражение вида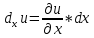 – называется частным дифференциалом функции u по переменной x.
– называется частным дифференциалом функции u по переменной x.
Сумма всех частных дифференциалов функции– называется полным дифференциалом функции: du=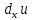 +
+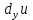
+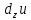 .
.
Примеры:
Частные производные: u=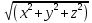
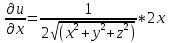
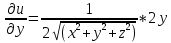
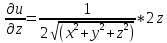
Частные дифференциалы: все тоже самое, умноженное на dx.
Пусть задана функция f(х,y,z), найдем ее частные производные: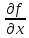 ,
, 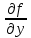 ,
,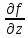 , тогда выражение вида :
, тогда выражение вида : 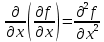 –называется чистой частной производной второго порядка,
–называется чистой частной производной второго порядка, 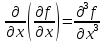 – чистая частная производная третьего порядка.
– чистая частная производная третьего порядка.
Пусть задана функция f(х,y,z), найдем ее частные производные: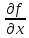 ,
, 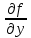 ,
,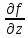 , тогда выражение вида:
, тогда выражение вида: 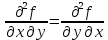 – называется смешанной частной производной второго порядка,
– называется смешанной частной производной второго порядка, 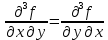 – смешанная частная производная третьего порядка.
– смешанная частная производная третьего порядка.
Примеры:
f(x,y,z)=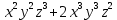
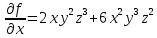 – частная производная по Х.
– частная производная по Х.
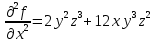 – частная производная второго порядка по Х.
– частная производная второго порядка по Х.
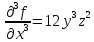 – частная производная третьего порядка по Х.
– частная производная третьего порядка по Х.
Теорема (о равенстве смешанных производных)
Пусть f(x.y) – определена вместе со своими частными производными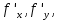
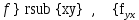 в некоторой окрестности точки (х0,у0), причем
в некоторой окрестности точки (х0,у0), причем 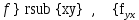 непрерывны в этой точке, тогда:
непрерывны в этой точке, тогда: 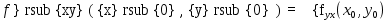 .
.
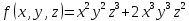
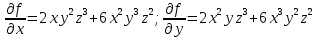
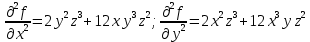
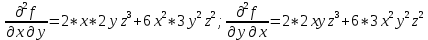
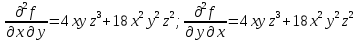
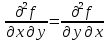
Дифференциалом функции z=f(x,y) называется сумма произведений частных производных этой функции на приращения независимых переменных
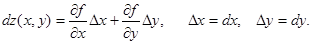
Функция z=f(x,y) называется дифференцируемойой в точке (х,у), если ее полное приращение может быть представлено в виде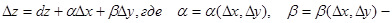 бесконечно малые величины при Δх→0, Δу→0.
бесконечно малые величины при Δх→0, Δу→0.
Дифференциалом 2го порядка функции z=f(x,y) называют дифференциал от дифференциала 1го порядка.
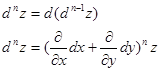
Рассмотрим сложную функцию у=f(u) , u=u(x), то есть у= f(u(х))= f(х). Тогда по определению дифференциала имеем dy=fх’(x)dx.
Но поскольку производная сложной функции равна fх’= fu’*ux’,то dy= fu’ *ux’ dx. Используя равенство ux’ dx=du, получим dy= fu’(u) du.
Необходимое условие экстремума. Если точка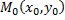 является точкой экстремума функции то
является точкой экстремума функции то 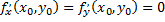 или хотя бы одна из этих производных не существует.
или хотя бы одна из этих производных не существует.
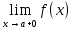 был равен
был равен 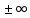 .
.Говорят, что прямая у=kx+b является наклонной асимптотой графика функции у=f(x) при х
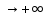 , если f(x) представима в виде: f(x)=kx+b+
, если f(x) представима в виде: f(x)=kx+b+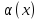 , где
, где 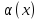 , бесконечно-малая функция, т.е
, бесконечно-малая функция, т.е 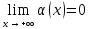 .
.Теорема (о существовании наклонной асимптоты)
Для того чтобы график функции у=f(x) имел при х
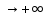 наклонную асимптоту необходимо и достаточно, чтобы существовали два предела:
наклонную асимптоту необходимо и достаточно, чтобы существовали два предела: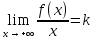 (1)
(1)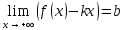 (2)
(2)Доказательство:
-
Необходимость.
Пусть график функции у=f(x) имеет наклонную асимптоту. Нужно доказать, что существуют два предела (1) и (2). По определению наклонной асимптоты имеем: f(x)=kx+b+
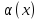 , где
, где 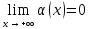 . Найдем:
. Найдем: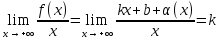 (1)
(1)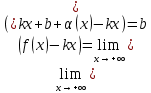 (2)
(2)-
Достаточность.
Даны два предела (1) и (2). Нужно доказать, что f(x)=kx+b+
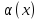 . Из (2)
. Из (2)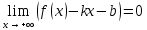 , означает что
, означает что 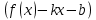 – бесконечно малая функция. Обозначим ее через
– бесконечно малая функция. Обозначим ее через 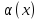 =
=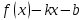 . Следовательно, f(x)=kx+b+
. Следовательно, f(x)=kx+b+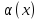 , откуда следует, что у=f(x) – имеет наклонную асимптоту.
, откуда следует, что у=f(x) – имеет наклонную асимптоту. -
Опишите схему полного исследования функции с помощью производной и построения её графика.
Схему полного исследования функции с помощью производной и построения её графика.
-
Найти область определения ф-ции и, если возможно, область изменения ф-ции. -
Исследовать ф-цию на четность, нечетность, периодичность. -
Найти точки пересечения графика ф-ции с осями координат и интервалы знакопостоянства ф-цию. -
Исследовать функцию на непрерывность. Найти точки разрыва (если они существуют) и установить их характер. -
Исследовать поведение ф-ции на концах области определения. -
Определить интервалы монотонности (возрастания и убывания) ф-ции: найти точки экстремума и ф-ции. -
Определить интервалы выпуклости вниз и выпуклости вверх графика ф-ции; найти точки перегиба и значения ф-ции в этих точках. -
Найти асимптоты графика ф-ции (вертикальные, горизонтальные, наклонные y=kx+b)
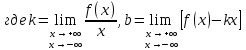
-
Взять несколько контрольных точек. -
Построить график ф-ции.
- Сформулируйте определение частной производной функции трех переменных в точке. Введите понятие частного и полного дифференциалов функции в точке. Приведите примеры нахождения частных производных и частных дифференциалов функции трех переменных.
Пусть в некоторой окрестности точки (х0,y0,z0) задана функция u=u(х,y,z), фиксируя переменные y и z: y=y0, z=z0 , получим функцию одной переменной х: u=u(х,y0,z0). Обычная производная этой функции по х в точке х0 называется частной производной функции.
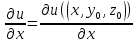
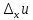 = u(x0+
= u(x0+ , y0,z0)-u(х0,y0,z0) – приращение функции u по переменной x
, y0,z0)-u(х0,y0,z0) – приращение функции u по переменной x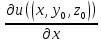 =
=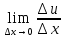
Пусть u=u(х,y,z), тогда выражение вида
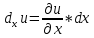 – называется частным дифференциалом функции u по переменной x.
– называется частным дифференциалом функции u по переменной x.Сумма всех частных дифференциалов функции– называется полным дифференциалом функции: du=
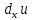 +
+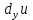
+
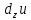 .
.Примеры:
Частные производные: u=
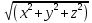
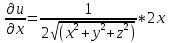
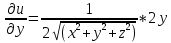
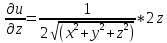
Частные дифференциалы: все тоже самое, умноженное на dx.
- 1 ... 5 6 7 8 9 10 11 12 ... 15
Введите понятие частных производных второго и третьего порядков (чистых и смешанных). Приведите примеры нахождения частных производных второго и третьего порядков.
Пусть задана функция f(х,y,z), найдем ее частные производные:
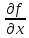 ,
, 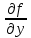 ,
,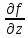 , тогда выражение вида :
, тогда выражение вида : 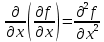 –называется чистой частной производной второго порядка,
–называется чистой частной производной второго порядка, 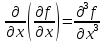 – чистая частная производная третьего порядка.
– чистая частная производная третьего порядка.Пусть задана функция f(х,y,z), найдем ее частные производные:
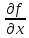 ,
, 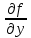 ,
,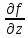 , тогда выражение вида:
, тогда выражение вида: 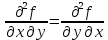 – называется смешанной частной производной второго порядка,
– называется смешанной частной производной второго порядка, 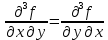 – смешанная частная производная третьего порядка.
– смешанная частная производная третьего порядка.Примеры:
f(x,y,z)=
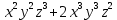
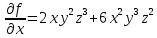 – частная производная по Х.
– частная производная по Х.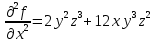 – частная производная второго порядка по Х.
– частная производная второго порядка по Х.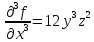 – частная производная третьего порядка по Х.
– частная производная третьего порядка по Х.-
Сформулируйте теорему о равенстве смешанных частных производных второго порядка. Приведите примеры.
Теорема (о равенстве смешанных производных)
Пусть f(x.y) – определена вместе со своими частными производными
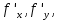
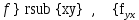 в некоторой окрестности точки (х0,у0), причем
в некоторой окрестности точки (х0,у0), причем 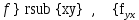 непрерывны в этой точке, тогда:
непрерывны в этой точке, тогда: 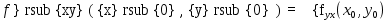 .
.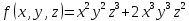
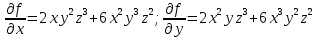
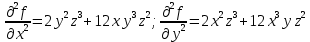
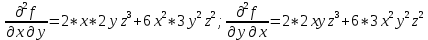
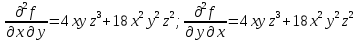
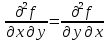
- Введите понятие дифференциалов высших порядков функции двух переменных. Опишите процесс нахождения дифференциалов второго и третьего порядков. Объясните, в чем особенность нахождения дифференциала второго порядка сложной функции. Приведите примеры.
Дифференциалом функции z=f(x,y) называется сумма произведений частных производных этой функции на приращения независимых переменных
Функция z=f(x,y) называется дифференцируемойой в точке (х,у), если ее полное приращение может быть представлено в виде
Дифференциалом 2го порядка функции z=f(x,y) называют дифференциал от дифференциала 1го порядка.
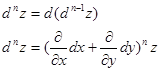
Рассмотрим сложную функцию у=f(u) , u=u(x), то есть у= f(u(х))= f(х). Тогда по определению дифференциала имеем dy=fх’(x)dx.
Но поскольку производная сложной функции равна fх’= fu’*ux’,то dy= fu’ *ux’ dx. Используя равенство ux’ dx=du, получим dy= fu’(u) du.
-
Сформулируйте необходимые условия существования экстремума функции двух переменных в точке. Опишите достаточные условия строгого экстремума функции двух переменных в точке. Объясните алгоритм нахождения экстремума функции двух переменных в точке.
Необходимое условие экстремума. Если точка
