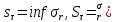Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 81
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 группа. Интегралы, подынтегральная функция которых в виде множителя содержит: ln x, arcsin x, arccos x, arctg x, arctg x2 и др., при этом оставшаяся часть функции является производной известной функции.
2 группа.
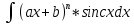 ,
,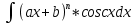 ,
, 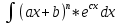 и др. За u=ax+b и путем n-кратного интегрирования по частям получаем результат.
и др. За u=ax+b и путем n-кратного интегрирования по частям получаем результат.3 группа.
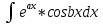 ,
,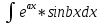 ,
,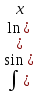 ,
,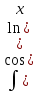 и др, берутся путем двухкратного интегрирования по частям и приведения интеграла к самому себе.
и др, берутся путем двухкратного интегрирования по частям и приведения интеграла к самому себе.Обозначаем данный интеграл за I и интегрируем по частям. Приходим к линейному уравнению относительно I, решая его, находим I (приведение интеграла к самому себе).
- Объясните, что такое рациональная дробь, правильная (неправильная) дробь, элементарная (простейшая) дробь. Опишите схему интегрирования правильных рациональных дробей. Проиллюстрируйте на конкретном примере.
Рациональной дробью с действительными(вещественными) коэффициентами называется отношение двух алгебраических многочленов Pn(x)/Qm(x) с действительными коэффициентами. Если n
Элементарными дробями называются дроби 4 типов:
-
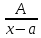 2)
2) 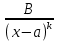 3)
3) 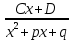 4)
4) 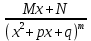
Теорема. Каждая правильная дробь может быть представлена в виде суммы конечного числа элементарных дробей.
Метод неопределенных коэффициентов.
-
Установить, что дробь правильная -
Если правильная разложить знаменатель -
Представить подынтегральную дробь в виде элементарных дробей с буквенными коэффициентами -
Привести к общему знаменателю и опустить его -
Приравнять коэффициенты при одинаковых степенях -
Подставить вместо А,B,C числа и проинтегрировать
- 1 ... 7 8 9 10 11 12 13 14 15
Опишите типы элементарных (простейших) рациональных дробей и сформулируйте правила их интегрирования. Приведите примеры. Опишите общую схему интегрирования рациональных функций.
Элементарными (простейшими) рациональными дробями будем называть дроби следующих четырех видов:
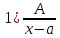 2)
2)  3)
3)  4)
4) 
Дроби 1 и 2 вида называются дробями 1-го рода. А вида 3 и 4 дробями 2-го рода.
Рассмотрим интегрирование этих дробей

Дроби вида 3 и 4 интегрируются с помощью подстановки, которая определяется в результате выделения квадрата двучлена из трехчлена х^2+px+g.

Таким образом интеграл от каждой элементарной дроби выражается через элементарные функции или как принято говорить каждая элементарная дробь может быть проинтегрирована в конечном виде.
Алгоритм интегрирования рациональных функций
1. Установить какая это дробь – правильная или неправильная.
2. Если рациональная дробь неправильная, то надо выделить ее целую часть делением числителя на знаменатель.
3. Правильную дробь разложить на элементарные дроби применяя метод неопределенных коэффициентов или другие методы.
4.Проинтегрировать целую часть и сумму элементарных дробей.
5. Записать результат интегрирования данной рациональной функции.
- Объясните правила интегрирования рациональных тригонометрических выражений, применение универсальной тригонометрической подстановки и формул тригонометрии, правила вычисления интегралов вида
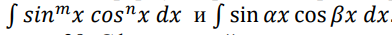 . Приведите примеры.
. Приведите примеры.
Интегрирование любого рационального выражения тригонометрических функций можно всегда свести к интегрированию алгебраической рациональной функции, используя универсальную тригонометрическую подстановку x=2arctant (или t=tg x/2), dx=2dt/1+t
2
Для преобразования рациональных выражений от sinx, cosx, tanx, cotx, secx и cscx в алгебраические рациональные функции переменной t применяются следующие тригонометрические формулы:
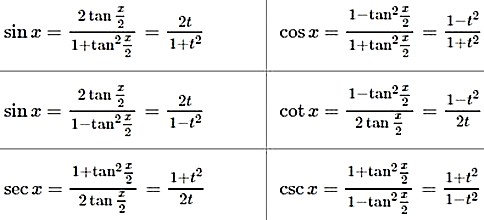
Универсальная тригонометрическая подстановка приводит к большим вычисления поэтому можно использовать u=sinx, u=cosx,u=tgx
Чтобы вычислить интеграл вида ∫sinnxcosmxdx, если n-нечетное то t=cosx, если m-нечетное то t=sinx
Для вычисления интеграла вида ∫R(sinx)cosxdx, где обе функции sinx и cosx входят в четной степени, то целесообразно использовать формулы понижения степени
Интегралы вида
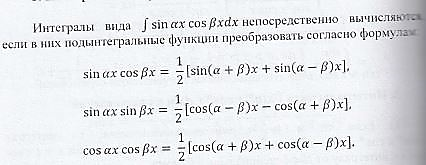
- Сформулируйте задачи, приводящие к понятию определенного интеграла, и объясните метод их решения. Введите понятия интегральной суммы Римана и понятие определенного интеграла. Сформулируйте необходимое условие интегрируемости по Риману и докажите его.
Определить путь S0 пройденный материальной точкой за промежуток времени от t0 до T, если известна u движения точки как функция времени u(t).
Решение. Разобьем промежуток времени произвольным образом на n частей. В любом из частичных промежутков ti,ti+1, выберем произвольный момент времени τi, вычислим скорость Ui=f(τi).
S= Ui Δti, а весь путь So=
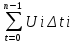 =
=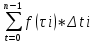
Это приближенное равенство будет тем точнее чем мельче дробление промежутка, когда λ=max{Δti
} будет стремится к нулю получим So=

Сумма вида
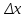 и высотами f(ξ).
и высотами f(ξ).Определение5. Если существует конечный предел I интегральной суммы при λ →0, не зависящий ни от способа разбиения отрезка [а, b] на части, ни от выбора точек ξ, то этот предел называется определенным интегралом функции f(x) на отрезке (а, b) и обозначается символом I=
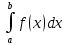 или
илиНеобходимое условие интегрируемости. Если функция интегрируема на отрезке [a; b], то она ограничена на этом отрезке.
Доказательство. Если функция неограниченна на отрезке [a; b], то она не ограничена хотя бы на одном отрезке разбиения, и слагаемое интегральной суммы может быть сделано как угодно большим, что противоречит ограниченности сумм.
Пример
Разрывная интегрируемая функция
 | |
- 1 ... 7 8 9 10 11 12 13 14 15
Опишите понятия верхней и нижней сумм Дарбу. Сформулируйте их свойства. Введите понятия верхнего и нижнего интегралов Дарбу. Сформулируйте критерий интегрируемости Дарбу.
Пусть f(x) определена и непрерывна на отрезке [a,b]. Пусть
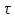 – некоторое разбиение отрезка [a,b] точками
– некоторое разбиение отрезка [a,b] точками 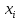
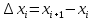 , i=0,1,2,... n-1
, i=0,1,2,... n-1Тогда по теореме Вейерштрасса f(x) ограничена на [a,b] и достигает на нем своей верхней и нижней граней, а значит она ограничена и на любом частичном отрезке [
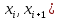 разбиения.
разбиения.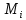 =sup f(x),
=sup f(x), 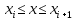
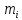 = inf f(x),
= inf f(x), 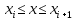
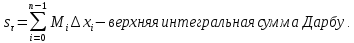
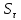
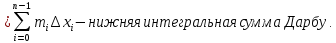
Свойства:
1. Если f-ограничена, то при любом разбиение
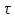 суммы,
суммы, 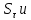
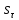 определена.
определена.2.Для любого разбиения
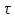 при любом выборе точек
при любом выборе точек 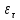 на [
на [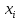 ,
, 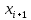 ]
]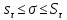
3. Если
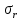 –какая-либо интегральная сумма Римана, соответствующая разбиению
–какая-либо интегральная сумма Римана, соответствующая разбиению