Файл: Нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 110
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа № 4
Тема: Вычисление и сравнение логарифмов. Логарифмирование и потенцирование выражений
Продолжительность: 1 час
Материалы для подготовки к практической работе:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 2 Занятие 4; -
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Логарифмы. Свойства логарифмов: https://resh.edu.ru/subject/lesson/5753/main/272579/
2. Десятичные и натуральные логарифмы: https://resh.edu.ru/subject/lesson/3823/main/198629/
Образец работы:
| Вариант 1 | Вариант 2 | ||||||||||
| (6 баллов) Задание 1. Найдите область определения выражения. | |||||||||||
|
| ||||||||||
| (8 баллов) Задание 2. Вычислите, используя определение логарифма, основное логарифмическое тождество, свойства логарифмов. | |||||||||||
| 1) 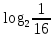 ; 2) ; 2) 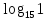 ; 3) ; 3) 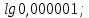 4) 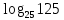 ; 5) ; 5)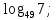 6) 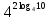 ; 7) ; 7) 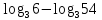 ; ;8) 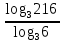 ; 9) ; 9) 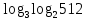 ; ;10) 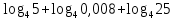 . . | 1); 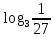 2) 2) 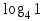 ; 3) ; 3) 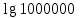 ; ;4) 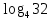 ; 5) ; 5)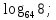 6) 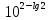 ; 7) ; 7) 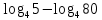 ; ;8) 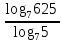 ; 9) ; 9) 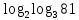 ; ;10) 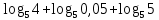 . . | ||||||||||
| (7 баллов) Задание 3. Сравните числа. | |||||||||||
| 1) 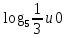 ; 2) ; 2) 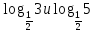 ; ;3) 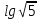 и и 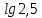 ; ; 4) 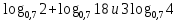 . . | 1) 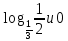 ; 2) ; 2) 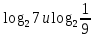 ; ; 3) 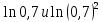 ; ;4) 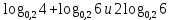 . . | ||||||||||
| | Критерии оценивания:
| ||||||||||
Контрольная работа № 2
Тема: Корни, степени и логарифмы
Продолжительность: 1 час
Материалы для подготовки к контрольной работе:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 2 Занятия 2-4, 6. -
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Корень n-ой степени:https://resh.edu.ru/subject/lesson/5498/main/272546/
2. Степень с рациональным показателем. Степень с действительным показателем:
https://resh.edu.ru/subject/lesson/4729/main/159017/
3. Логарифмы. Свойства логарифмов: https://resh.edu.ru/subject/lesson/5753/main/272579/
4. Десятичные и натуральные логарифмы: https://resh.edu.ru/subject/lesson/3823/main/198629/
5. Иррациональные уравнения: https://resh.edu.ru/subject/lesson/5569/main/159267/
6. Показательная функция:https://resh.edu.ru/subject/lesson/3841/main/225577/
7. Показательные уравнения: https://resh.edu.ru/subject/lesson/5627/main/159325/
8. Логарифмическая функция: https://resh.edu.ru/subject/lesson/3834/main/198660/
9. Логарифмические уравнения: https://resh.edu.ru/subject/lesson/4732/main/198846/
Образец работы:
| Вариант 1 | Вариант 2 | ||||||||||
| (12 баллов) Задание 1.Найдите значение числового выражения. | |||||||||||
| а) 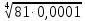 ; б) ; б) 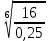 ; в) 7+ ; в) 7+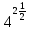 ; ;г) 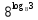 ; д) ; д) 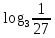 ; е) ; е) 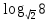 . .ж) 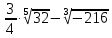 ; ;з) 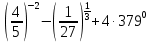 ; ;и)  . . | а) 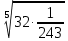 ; б) ; б) 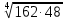 ; в) 47– ; в) 47–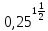 ; ;г) 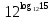 ; д) ; д) 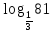 ; е) ; е) 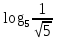 . .ж) 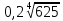 + +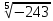 ; ;з) 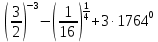 ; ;и). 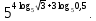 | ||||||||||
| (4 балла) Задание 2.Упростите выражения. | |||||||||||
| а) 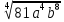 ; б) ; б)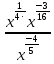 . . | а) 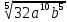 ; б) ; б) 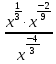 | ||||||||||
| (8 баллов) Задание 3.Решите уравнения. | |||||||||||
| а) 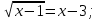 б) 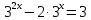 ; ;в) 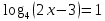 . . | а) 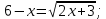 б) 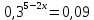 ; ;в) 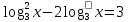 . . | ||||||||||
| | Критерии оценивания:
| ||||||||||
Образец выполнения работы:
| Задание с решением | Комментарии |
| Задание 1.Найдите значение числового выражения. | |
| а) 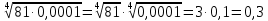 б) 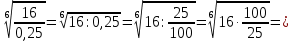 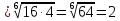 в) 7+ 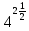 =7+ =7+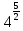 =7+ =7+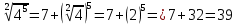 г) 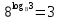 д) 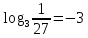 е) 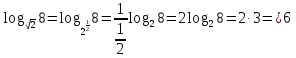 ж) 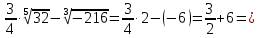 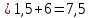 з) 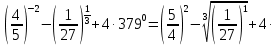 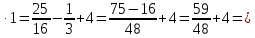 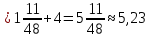 и) 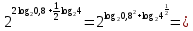 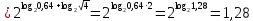 | Применим свойство корня n-ой степени: 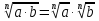 Извлекая корни, задаем вопрос: какое число в 4-ой степени даст 81? 0,0001? ________________________________________ Рассуждаем так: 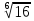 не извлекается точно, только приближенно. Выполним деление под знаком корня, извлечем корень из получившегося числа не извлекается точно, только приближенно. Выполним деление под знаком корня, извлечем корень из получившегося числа______________________________________ Знаем, что 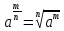 , применим определение ко 2-му слагаемому , применим определение ко 2-му слагаемомуЗнаем свойство корня n-ой степени: 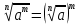 , применим его , применим его_______________________________________ Воспользуемся основным логарифмическим тождеством: 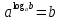 ___________________________________ Воспользуемся определением логарифма, зададим вопрос: в какую степень нужно возвести 3, чтобы получить 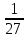 ______________________________________ Преобразуем основание логарифма, используя определение степени с рациональным показателем: 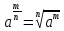 . Справа налево . Справа налево 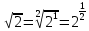 Воспользуемся свойством логарифмов: 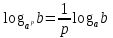 . .Вычислим логарифм, задав вопрос: в какую степень нужно возвести 2, чтобы получилось 8? Это 3. ________________________________________ Извлечем корни задав вопросы: 1) Какое число в 5-ой степени даст 32? 2) Какое число в 3-ей степени даст -216? _____________________________________ Найдем значение каждого слагаемого: 1) 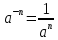 (дробь переворачивается) (дробь переворачивается)2) 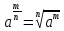 3) 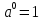 ______________________________________ Выполним преобразования в показателе степени: 1) воспользуемся формулой: 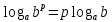 справа налево справа налево2) применим свойство логарифмов: 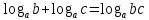 Вспомним основное логарифмическое тождество: 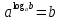 , запишем ответ , запишем ответ |
| Задание 2.Упростите выражения. | |
| а) 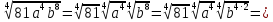 =3a 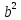 б) 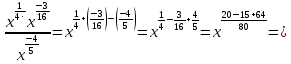 = 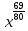 . . | Применим свойства корня n-ой степени: 1) 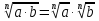 2) 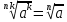 _______________________________________ Воспользуемся свойствами степени: 1) 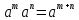 2) 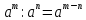 Выполним вычисления. |
| Задание 3.Решите уравнения. | |
| а) 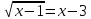 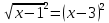 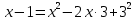 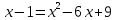 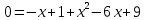 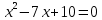 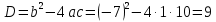 , уравнение имеет 2 различных корня , уравнение имеет 2 различных корня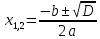 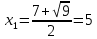 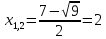 Проверка: При 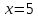 получим: получим: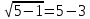 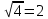 – верно – верно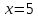 – корень иррационального уравнения – корень иррационального уравненияПри 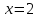 получим: получим: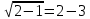 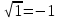 – неверно – неверно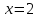 – посторонний корень – посторонний кореньОтвет: 5. б)  Замена: Пусть 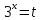 , тогда , тогда 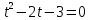 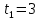 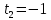 Обратная замена: 1) 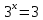 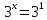 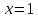 2) 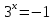 – корней нет – корней нетОтвет: 1. в) 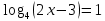 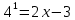 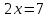 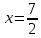 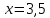 Ответ: 3,5. г) 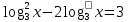 Замена: Пусть 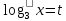 , тогда , тогда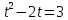 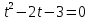 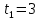 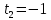 Обратная замена: 1) 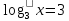 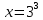 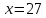 2) 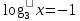 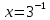 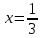 Ответ: 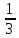 , 27. , 27. | Основной метод решения иррациональных уравнений - возведение обеих частей в соответствующую степень. В данном случае - во 2. Вспомним, что 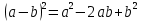 . .Решим квадратное уравнение При возведении четную степень могли возникнуть посторонние корни. Сделаем проверку, подставив найденные корни квадратного уравнения в исходное (1-я строка) иррациональное уравнение _____________________________________ Сделаем замену Решим квадратное уравнение Сделаем обратную замену: 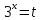 ____________________________________ Воспользуемся определением логарифма: 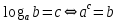 Решим линейное уравнение. ______________________________________ Сделаем замену Решим квадратное уравнение Сделаем обратную замену: 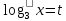 |
Тема 3. Прямые и плоскости в пространстве
Практическая работа № 5
Тема: Взаимное расположение прямых и плоскостей. Перпендикуляр и наклонная к плоскости. Угол между прямой и плоскостью. Теоремы о взаимном расположении прямой и плоскости. Теорема о трех перпендикулярах
Продолжительность: 1 час
Материалы для подготовки к практической работе:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 3 Занятия1-3; -
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Введение в стереометрию:https://resh.edu.ru/subject/lesson/4756/main/203546/
2. Параллельность прямых, прямой и плоскости: https://resh.edu.ru/subject/lesson/6065/main/125655/
3) Параллельность плоскостей: https://resh.edu.ru/subject/lesson/6129/main/131676/
4) Перпендикулярность прямой и плоскости: https://resh.edu.ru/subject/lesson/4724/main/20415/
Образец работы:
| Вариант 1 | Вариант 2 | ||||||||||
| (6 баллов) Задание 1. На рисунке изображена треугольная пирамида. Назовите: а) плоскости, в которых лежат прямые DB, PE, AB, MK, CВ; б) точки пересечения прямой DK с плоскостью ABC, прямой CE с плоскостью ADB; в) прямые, по которым пересекаются плоскости ABC и DCB, ABD и CDA. 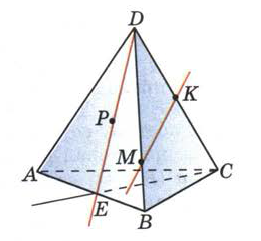 | (6 баллов) Задание 1. На рисунке изображен куб. Назовите: а) плоскости, в которых лежат прямые АА1, KM, DR, QB, AB; б) точки пересечения прямой МК с плоскостью ABD, прямой BP плоскостью A1B1C1; в) прямые, по которым пересекаются плоскости AA1B1 и ACD, PB1C1 и ABC; 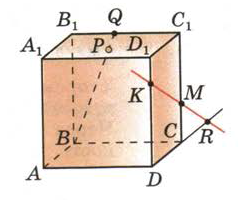 | ||||||||||
| (4 балла)Задание 2. Решите задачу. | |||||||||||
| Из точки A к плоскости α проведены перпендикуляр и наклонная, длины которых равны соответственно 4 см и 5 см. Найдите длину проекции наклонной. | Из точки A к плоскости α проведены перпендикуляр и наклонная, длины которых равны соответственно 3 см и 5 см. Найдите длину проекции наклонной. | ||||||||||
| (6 баллов)Задание 3. Решите задачу. | |||||||||||
| Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если они относятся друг к другу как 1:2, а проекции наклонных равны 1 см и 7 см. | Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если они относятся друг к другу как 1:3, а проекции наклонных равны 1 см и 8 см. | ||||||||||
| | Критерии оценивания:
| ||||||||||
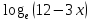 2)
2) 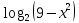
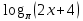 2)
2)