Файл: Нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 122
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Образец выполнения работы:
| Задание | Решение | Комментарий | ||||
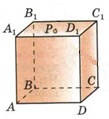
| (6 баллов) Задание 1. На рисунке изображен куб. Назовите: а) плоскости, в которых лежат прямые DB, AB1, C1В; б) точки пересечения прямой C1А с плоскостью DBC, прямой B1D1 с плоскостью AA1D; в) прямые, по которым пересекаются плоскости ABC и DCD1, D1BD и AA1B. 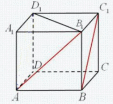 | № 1 а) 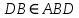 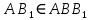 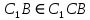 б) 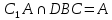 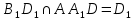 в) 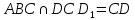 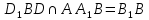 | а) Проведем прямую 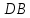 . Она лежит в плоскости нижнего основания куба . Она лежит в плоскости нижнего основания куба 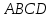 , любыми тремя из 4-х букв можно обозначить плоскость , любыми тремя из 4-х букв можно обозначить плоскость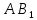 лежит в плоскости грани куба лежит в плоскости грани куба 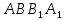 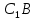 лежит в плоскости грани куба лежит в плоскости грани куба 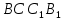 б) Проведем прямую  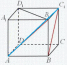 Плоскость 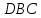 – это плоскость нижнего основания куба – это плоскость нижнего основания куба 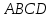 . Общей точкой является точка A. . Общей точкой является точка A.Плоскость 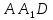 – это плоскость грани куба – это плоскость грани куба 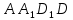 . Общая с прямой . Общая с прямой 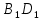 точка – точка – 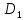 . .в) Плоскость 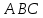 – это плоскость нижнего основания куба – это плоскость нижнего основания куба 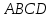 . .Плоскость 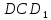 – это плоскость грани куба – это плоскость грани куба 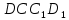 . .Общая прямая – 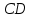 . .Плоскость 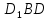 – это плоскость сечения куба – это плоскость сечения куба 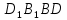 (проводим дополнительно прямую (проводим дополнительно прямую 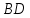 ) )Плоскость 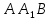 – это плоскость грани куба – это плоскость грани куба 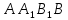 . .Общая прямая – 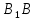 . . | ||||
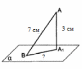
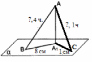
| (4 балла)Задание 2. Решите задачу. Из точки A к плоскости α проведены перпендикуляр и наклонная, длины которых равны соответственно 3 см и 7 см. Найдите длину проекции наклонной. |
Решение: 1) Рассмотрим треугольник 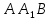 в соответствующей плоскости (плоскость существует по теореме "О существовании плоскости, проходящей через 3 данные точки") в соответствующей плоскости (плоскость существует по теореме "О существовании плоскости, проходящей через 3 данные точки")2) 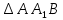 – прямоугольный, – прямоугольный, 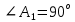 ( 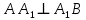 по определению прямой перпендикулярной плоскости, т.к. по определению прямой перпендикулярной плоскости, т.к. 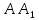 – перпендикуляр к – перпендикуляр к 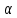 по условию) по условию)3) По теореме Пифагора: 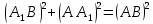 Откуда, 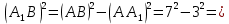 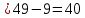 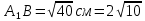 см смОтвет:  см. см. | Аналогично по известным перпендикуляру и проекции наклонной можно отыскать саму наклонную; по известным наклонной и проекции наклонной найти длину перпендикуляра. Отличаться в решении будет только 3 пункт Для обоснования существования плоскости может быть использовано другое утверждение | ||||
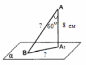
| (6 баллов) Задание 3. Решите задачу. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если они относятся друг к другу как 1:4, а проекции наклонных равны 1 см и 8 см. |
По теореме Пифагора: 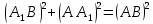 Откуда, 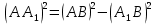 IV. Из того, что 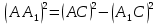 и и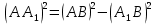 , следует: , следует: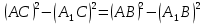 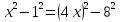 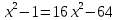 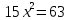 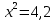 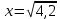 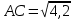 см см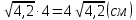 – длина наклонной – длина наклонной 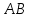 Ответ: 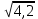 см, см, 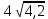 см. см. | Извлекаем корень с положительным значением, т.к. находим длину. | ||||
Практическая работа № 6
Тема: Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве
Продолжительность: 1 час
Материалы для подготовки к практической работе:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 3 Занятие 1-3;
Образец работы:
| Вариант 1 | Вариант 2 | ||||||||||
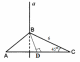
| (2 балла) Задание 1. Прямая А перпендикулярна плоскости АВС. Найдите расстояние между прямымиа и АС. | |||||||||||
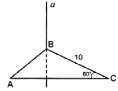 | 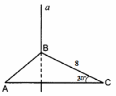 | ||||||||||
| (4 балла) Задание 2. Решите задачу: | |||||||||||
| Двугранный угол равен 60о. Точка, выбранная на одной из граней, удалена от ребра угла на 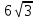 см. Найдите расстояние от этой точки до другой грани. см. Найдите расстояние от этой точки до другой грани. | Двугранный угол равен 60о. Точка, выбранная на одной из граней, удалена от ребра угла на 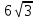 см. Найдите расстояние от этой точки до другой грани. см. Найдите расстояние от этой точки до другой грани. | ||||||||||
| | Критерии оценивания:
| ||||||||||
Образец выполнения работы:
| Задание | Решение | ||||
| (2 балла) Задание 1. Прямая a перпендикулярна плоскости АВС. Найдите расстояние между прямымиа и АС. |
| ||||
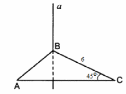 | |||||
| (4 балла) Задание 2. Решите задачу: |
| ||||
| Двугранный угол равен 30о. Точка, выбранная на одной из граней, удалена от ребра угла на 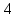 см. Найдите расстояние от этой точки до другой грани. см. Найдите расстояние от этой точки до другой грани. | |||||
Тестирование № 1
Тема: Параллельное проектирование и его свойства. Взаимное расположение пространственных фигур
Продолжительность: 1 час
Материалы для подготовки к тестированию:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 6 Занятие 1; -
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Параллельность прямых, прямой и плоскости: https://resh.edu.ru/subject/lesson/6065/main/125655/
2.Взаимное расположение прямых в пространстве: https://resh.edu.ru/subject/lesson/6133/start/272668/
3. Параллельность плоскостей: https://resh.edu.ru/subject/lesson/6129/main/131676/
4. Перпендикулярность прямой и плоскости: https://resh.edu.ru/subject/lesson/4724/main/20415/
5. Перпендикулярность плоскостей: https://resh.edu.ru/subject/lesson/4748/start/20810/
Образец работы:
1. Выбери фигуры, которые могут быть параллельными проекциями двух параллельных прямых.
-
прямая -
точка -
луч -
две параллельные прямые -
две точки -
отрезок
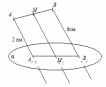
2. Известно, что I - проецирующая прямая параллельного проецирования. АВ и CD – отрезки, причем AB∥CD, AB∦I, CD∦I. Укажите взаимное расположение проекций A1B1 и C1D1 отрезков АВ и CD на плоскости α.
-
A1B1∥C1D1 -
A1B1∩C1D1 -
A1B1⊂C1D1 -
C1D1⊂A1B1 -
A1B1 и C1D1 скрещиваются
3. Дано I - направление параллельного проецирования, АВАВ∦I. Выбери фигуру, которая может быть проекцией отрезка АВ.
-
прямая -
точка -
две точки -
луч -
отрезок
4. Дано I - направление параллельного проецирования, a∩b=O, a∦I, b∦I. Укажи фигуры, которые могут быть проекциями прямых а и b.
-
одна прямая -
две пересекающиеся прямые -
две параллельные прямые -
две скрещивающиеся прямые -
угол
5. Укажите фигуры, в которые может проецироваться квадрат ABCD.
-
параллелограмм -
прямоугольник -
трапеция -
ромб -
квадрат -
отрезок
6. Прямая параллельного проецирования не параллельна плоскости фигуры. Соотнесите фигуры и проекции.
-
прямоугольник -
квадрат -
прямоугольный треугольник -
равнобедренная трапеция -
ромб -
равнобедренный треугольник -
параллелограмм
7. Известно, что четырехугольник A1B1C1D1 является параллельной проекцией трапеции ABCD (BC∥AD) на плоскость α. Определите вид четырехугольника A1B1C1D1.
-
ромб -
параллелограмм -
трапеция (A1B1∥C1D1) -
трапеция (A1D1∥B1C1) -
прямоугольник
8. Известно, что △A1B1C1 является параллельной проекцией △ABC на плоскость α; АМ, АК, АН - медиана, биссектриса, высота △АВС соответственно; М1, К1, Н1 - проекции точек М, К, Н соотвественно на плоскость α. Укажите правильные утверждения.
-
Если △АВС - правильный, то △А1В1С1 - правильный. -
Если △АВС - прямоугольный, то △А1В1С1 - прямоугольный. -
Если АМ - медиана △АВС, то А1М1 - медиана △А1В1С1. -
Если АК - биссектриса △АВС, то А1К1 - биссектриса △А1В1С1. -
Если АН - высота △АВС, то А1Н1 - высота △А1В1С1. -
Если ВК:КС=2:3, то В1К1:К1С1=2:3. -
Если А∠А=30∘ и ВС=20 см, то А∠А1=30∘ и В1С1=20 см.
Контрольная работа № 3
Тема: Прямые и плоскости в пространстве
Продолжительность: 1 час
Материалы для подготовки к практической работе:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 3 Занятия1-3; -
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Введение в стереометрию:https://resh.edu.ru/subject/lesson/4756/main/203546/
2. Параллельность прямых, прямой и плоскости: https://resh.edu.ru/subject/lesson/6065/main/125655/
3.Взаимное расположение прямых в пространстве: https://resh.edu.ru/subject/lesson/6133/start/272668/
4. Параллельность плоскостей: https://resh.edu.ru/subject/lesson/6129/main/131676/
5. Перпендикулярность прямой и плоскости: https://resh.edu.ru/subject/lesson/4724/main/20415/
6. Перпендикуляр и наклонные: https://resh.edu.ru/subject/lesson/6127/start/221519/
7. Перпендикулярность плоскостей: https://resh.edu.ru/subject/lesson/4748/start/20810/
Образец работы:
| Вариант 1 | Вариант 2 | ||||||||||
| |||||||||||
 1) назовите прямые, по которым пересекаются плоскости AA1B1 и ACD, PB1C1 и ABC (PBB1C1C); 2) назовите плоскости, которым точка В принадлежит, не принадлежит; 3) определите в каком отношении находятся прямые AD и C1B1. |  1) назовите прямые, по которым пересекаются плоскости ABD и CDA, PDC и ABC; 2) назовите плоскости, которым точка В принадлежит, не принадлежит; 3) определите в каком отношении находятся прямые DB и AC. | ||||||||||
| (4 балла) Задание 2.Решите задачу. | |||||||||||
| Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен 600. Найдите наклонную и ее проекцию на данную плоскость, если перпендикуляр равен 8. | Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен 300. Найдите перпендикуляр и наклонную, если проекция наклонной равна 4. | ||||||||||
| (4 балла) Задание 3.Решите задачу: «Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1, М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и…». | |||||||||||
| АА1=2 см, ВВ1=6 см | АА1=9 см, ВВ1=7 см | ||||||||||
| (3 балла) Задание 4. Прямая МО перпендикулярна плоскости ΔАОВ. 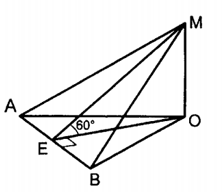 Найдите площадь ΔАОВ , если… | |||||||||||
| SΔAMB=8. | SΔAMB=12. | ||||||||||
| | Критерии оценивания:
| ||||||||||
Образец выполнения работы:
| Задача | Решение | ||
 1) назовите прямые, по которым пересекаются плоскости AA1B1 и ACD, PB1C1 и ABC (PBB1C1C); 2) назовите плоскости, которым точка В принадлежит, не принадлежит; 3) определите в каком отношении находятся прямые AD и C1B1. | 1) 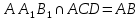 ; ;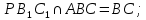 2) 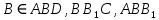 ; ;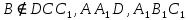 ; ;3) AD и C1B1 – параллельны (т.к. лежат в плоскости 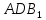 и не пересекаются) и не пересекаются) | ||
| (4 балла) Задание 2.Решите задачу. Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен 600. Найдите наклонную и ее проекцию на данную плоскость, если перпендикуляр равен 8 см. |
Решение: 1) Рассмотрим треугольник 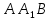 в соответствующей плоскости (плоскость существует по теореме "О существовании плоскости, проходящей через 3 данные точки") в соответствующей плоскости (плоскость существует по теореме "О существовании плоскости, проходящей через 3 данные точки")2) 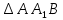 – прямоугольный, – прямоугольный, 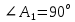 ( 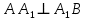 по определению прямой перпендикулярной плоскости, т.к. по определению прямой перпендикулярной плоскости, т.к. 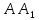 – перпендикуляр к – перпендикуляр к 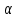 по условию) по условию)3) ∠A=60о⇒∠В=30о, 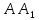 – катет, лежащий напротив угла в 30о⇒ – катет, лежащий напротив угла в 30о⇒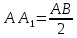 ⇒ ⇒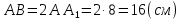 4) По теореме Пифагора: 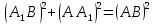 Откуда, 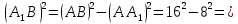 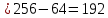 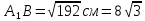 см смОтвет: 16 см, 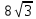 см. см. | ||
| (4 балла) Задание 3.Решите задачу: «Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1, М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и АА1=2 см, ВВ1=6 см». |
Решение: 1) Проведем плоскость β через 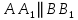 (такая плоскость обязательно существует по определению параллельных прямых); (такая плоскость обязательно существует по определению параллельных прямых);2) Прямые АВ, 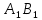 , ,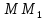 принадлежат β (по теореме о принадлежности прямой плоскости); принадлежат β (по теореме о принадлежности прямой плоскости);3) Рассмотрим в β четырехугольник 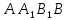 – трапецию (т.к. – трапецию (т.к. 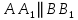 по условию и АВ по условию и АВ 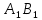 ,т.к. ,т.к. 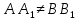 ) ; ) ;4) 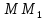 – средняя линия трапеции (в силу теоремы Фалеса и из того, что – средняя линия трапеции (в силу теоремы Фалеса и из того, что 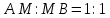 ); );5) 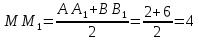 (см) (см)Ответ: 4 см. | ||
| (3 балла) Задание 4. Прямая МО перпендикулярна плоскости ΔАОВ. 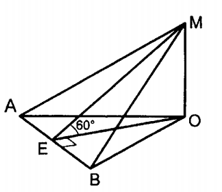 Найдите площадь ΔАОВ , если SΔAMB=8 дм2. |
Решение: ΔАОВ – ортогональная проекция  на соответствующую плоскость на соответствующую плоскостьПо формуле 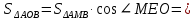 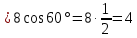 (дм2) (дм2)Ответ:  дм2. дм2. |
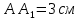
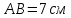
 – проекция наклонной
– проекция наклонной
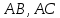 – наклонные к
– наклонные к 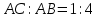
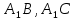 – проекции наклонных,
– проекции наклонных,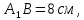
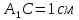
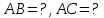
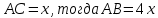 .
.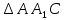 – прямоугольный,
– прямоугольный, 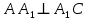 по определению прямой перпендикулярной плоскости, т.к.
по определению прямой перпендикулярной плоскости, т.к. 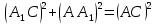
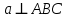 ,
, 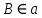
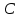 по условию, и не пересекаются, т.к.
по условию, и не пересекаются, т.к. 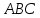 треугольник
треугольник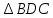 – прямоугольный (∠D=90о по построению), равнобедренный (∠С=45о по условию).
– прямоугольный (∠D=90о по построению), равнобедренный (∠С=45о по условию). 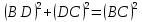
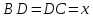 . Тогда
. Тогда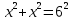
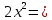 36
36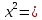 18
18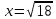
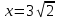
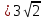
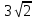 .
.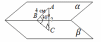
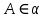 , АВ=4см
, АВ=4см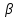
 – прямоугольный (∠С=90о по построению);
– прямоугольный (∠С=90о по построению);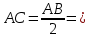
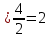 (см)
(см)
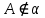
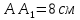
 – наклонная к
– наклонная к 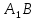 – проекция наклонной
– проекция наклонной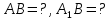
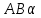
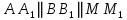
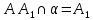
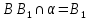
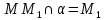
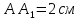
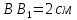
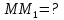
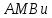 АОВ
АОВ