Файл: Нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 118
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема4. Комбинаторика
Практическая работа № 7
Тема: Правила комбинаторики. Решение комбинаторных задач. Размещения, сочетания и перестановки
Продолжительность: 1 час
Материалы для подготовки к практической работе:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 4 Занятия1-3; -
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Примеры комбинаторных задач: https://resh.edu.ru/subject/lesson/2572/start/
2. Перестановки: https://resh.edu.ru/subject/lesson/4927/start/285007/
3. Правило произведения. Размещения с повторениями: https://resh.edu.ru/subject/lesson/4028/start/37167/
4. Размещения без повторения: https://resh.edu.ru/subject/lesson/4045/start/149136/
5. Сочетания без повторений: https://resh.edu.ru/subject/lesson/6119/start/285193/
6. Сочетания с повторениями:https://resh.edu.ru/subject/lesson/4928/start/38164/
Образец работы:
| Вариант 1 1. Вычислите: а) 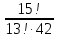 б) 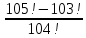 2. Сколькими способами можно расставить на полке девять разных книг? 3. В группе учатся 20 студентов. Сколькими способами можно выбрать старосту, его заместителя и ответственного за дежурства? 4. На занятии преподаватель проводит соревнование. Сколькими способами можно выбрать трех человек в жюри, если в группе 20 студентов? | Вариант 2 1. Вычислите: а) 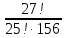 б) 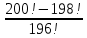 2. На полке стоят 5 различных книг. Сколькими способами можно положить 3 из них в стопку? 3. Каким количеством способов можно рассадить восемь человек в ряд из восьми стульев? 4. Сколькими способами можно выбрать в дозор трех солдат из 80? |
Практическая работа № 8
Тема: Бином Ньютона и треугольник Паскаля. Прикладные задачи
Продолжительность: 1 час
Материалы для подготовки к практической работе:
-
Конспект лекции по теме; -
Материалы учебника М.И. Башмакова Математика Глава 4 Занятие 3; -
Материалы портала «Российская электронная школа», доступные по ссылкам:
1. Бином Ньютона: https://resh.edu.ru/subject/lesson/6119/start/285193/
Образец работы:
| Вариант 1 1. Раскройте скобки в выражениях, рассчитав биномиальные коэффициенты по формуле числа сочетаний: а) 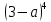 б) 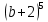 2. Раскройте скобки в выражении, воспользовавшись треугольников Паскаля:  . Найдите сумму всех биномиальных коэффициентов разложения. . Найдите сумму всех биномиальных коэффициентов разложения.4. У многочлена P найдите коэффициент при 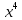 : :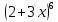 . . | Вариант 2 1. Раскройте скобки в выражениях, рассчитав биномиальные коэффициенты по формуле числа сочетаний: а)  б) 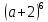 2. Раскройте скобки в выражении, воспользовавшись треугольников Паскаля: 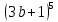 . Найдите сумму всех биномиальных коэффициентов разложения. . Найдите сумму всех биномиальных коэффициентов разложения.4. У многочлена P найдите коэффициент при 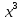 : :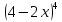 . . |
Образцы решения задач:
1. Раскройте скобки в выражениях, рассчитав биномиальные коэффициенты по формуле числа сочетаний:
а)
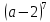 (Замечание: если в скобках записана разность, то в разложении знаки +/– чередуются)
(Замечание: если в скобках записана разность, то в разложении знаки +/– чередуются)б)
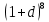
Решение:
а) Запишем формулу бинома Ньютона:
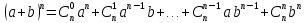
Тогда
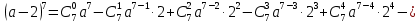
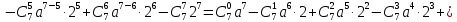
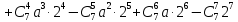
Вычислим биномиальные коэффициенты:
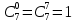
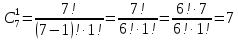
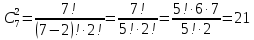
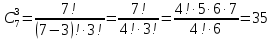

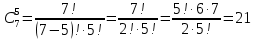
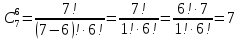
Подставим значения коэффициентов в разложение, вычислим значения степеней 2:
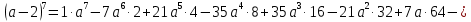
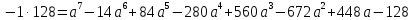
б) Запишем формулу бинома Ньютона:
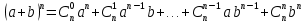
Тогда
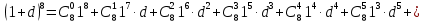
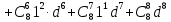
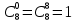
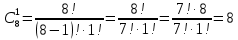
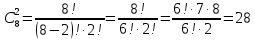

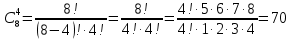
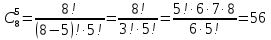
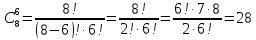
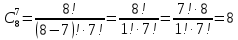
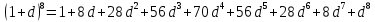
2. Раскройте скобки в выражении, воспользовавшись треугольником Паскаля:
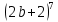 . Найдите сумму всех биномиальных коэффициентов разложения.
. Найдите сумму всех биномиальных коэффициентов разложения.Выпишем треугольник Паскаля:
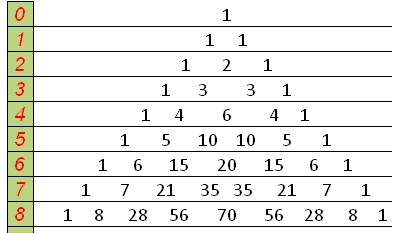
Коэффициенты 7 строки: 1, 7, 21, 35, 35, 21, 7, 1. Тогда
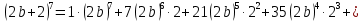
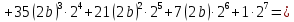
=
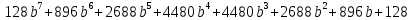
Найдем сумму всех биномиальных коэффициентов разложения:
(128+896+2688+4480)·2=17184
4. У многочлена P найдите коэффициент при
 :
: .
.Выпишем треугольник Паскаля:
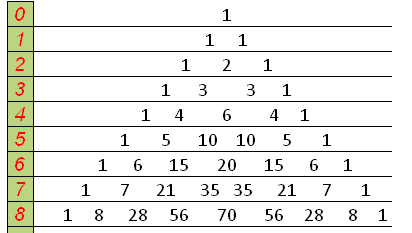
Коэффициенты 8 строки: 1, 8, 28, 56, 70, 56, 28, 8, 1. Тогда
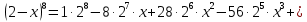
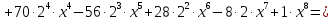
=

Коэффициент при
 :
: